15. Основные теоретические положения [1,2,4,5]
Для равновесия механической системы с идеальными связями необходимо и достаточно чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещение системы была равна нулю. Математически сформулированное условие равновесие выражается равенством:
Элементарная работа приложенной к телу силы F будет равен:
.
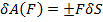Элементарная работа равна произведению вращающего момента на элементарный угол поворота:
δA(M)=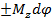 
,
где угол поворота равен:
.
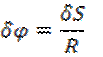ПРИМЕР 15.1
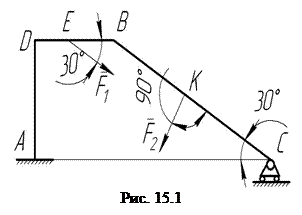Пользуясь принципом возможных перемещений, определить для составной конструкции, изображенной на схеме (рис.15.1), реактивный момент и вертикальную составляющую реакции заделки, если 
. 
, 
, 
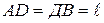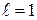м, 
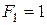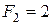кН, 
кН.
Рис.15.2
Решение:
Для определения реактивного момента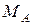 
заменим заделку в точке А шарнирно-неподвижной опорой, компенсировав отброшенную связь ее реакцией – реактивной парой сил с неизвестным моментом 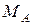(рис.15. 2).
Получившейся механической системе с одной степенью свободы даем возможное перемещение, повернув мысленно уголок АДВ на бесконечно малый угол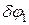 
, например по часовой стрелке. Точка В получит при этом возможное перемещение 
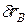, направленное перпендикулярно АВ и равное по модулю 
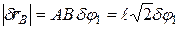; точка С получит возможное перемещение 
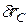, параллельное опорной плоскости шарнирно-неподвижной опоры С; стержень ВС повернется вокруг точки L – центра поворота, определенного как и МЦС в кинематике, как точка пересечения перпендикуляров, проведенных через точки В и С к направлениям их возможных перемещений. Угол 
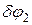, на который стержень ВС повернется вокруг точки L, определяется равенством:
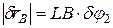, откуда
.
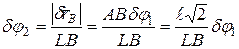Для нахождения 
воспользуемся теоремой синусов. Из 
(см. рис. 15.2):
.
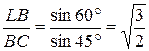Отсюда:
.
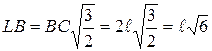Следовательно,
.
Теперь подсчитаем и приравняем к нулю сумму работ сил 
, 
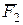и пары с моментом 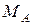при возможном перемещении системы.
Используя правило: работа сил, приложенных к вращающемуся телу, равна взятому с соответствующим знаком произведению момента сил относительно оси вращения на угол поворота. Поэтому:
.
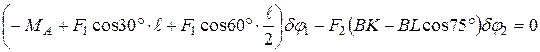Здесь в первых скобах записана сумма моментов силы и реактивной пары относительно точки А. Для определения момента силы она была разложена на вертикальную и горизонтальную составляющие. Со знаком плюс записаны моменты, направленные в сторону поворота 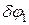. Момент пары записан со знаком минус, так как она стремится вращать уголок в направлении, противоположном возможному перемещению 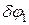. Во вторых скобках записано плечо силы 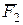относительно точки L. Знак минус перед второй скобкой поставлен потому, что сила 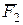стремится вращать стержень ВС вокруг точки L в направлении противоположном возможному перемещению .
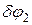Заменяя в предыдущем равенстве 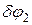его выражением через 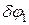и учитывая, что 
, 
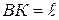, можем переписать его в виде:
.
Так как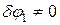 
, то отсюда:
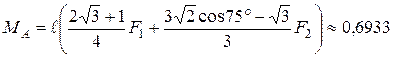кН×м.
Для нахождения вертикальной составляющей реакции заделки А заменим в исходной схеме заделку ползуном, который может перемещаться в вертикальном направлении и к которому жестко прикреплен угол АДВ, а отброшенную связь компенсируем вертикальной реакцией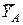 
(рис.15. 3).
Даем получившейся механической системе возможное перемещение, мысленно переместив угол АДВ поступательно вверх (
). Стержень ВС повернется вокруг центра поворота G на угол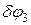 
. Уравнение принципа возможных перемещений запишется в виде:
,
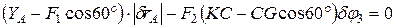откуда, учитывая, что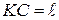 
, 
, 
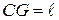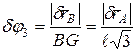, получаем
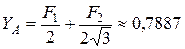кН.
ПРИМЕР 15.2
Для заданной секции (рис.15. 4) определить реакции в опорах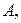 
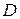и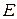 
, считая основание неразрывно связанным с почвой. Геометрические размеры и силовые показатели приведены в таблице 15.1
.
Таблица 15.1
Исходные данные для примера 15.2
| АВ, м | ВС, м | СD, м | q1, кН/м | q2, кН/м | q3, кН/м | q4, кН/м |
| 2,5 | 3,0 | 2,2 | 3,0 | 2,5 | 3,4 | 2,0 |
Заменим действие распределенных нагрузок сосредоточенными силами:
.
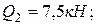
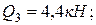
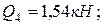
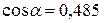В соответствии с этим расчетная схема секции примет вид рисунка 15.4.
Реакция опоры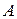 
представляет собой совокупность двух составляющих 
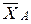и 
. Для определения горизонтальной составляющей 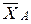цилиндрический шарнир 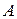мысленно заменим ползуном, дающим возможность перемещения точки 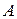в горизонтальном направлении. Придадим системе возможное перемещение 
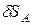под действием реакции 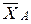. В этом случае, звено 
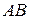примет положение 
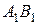, переместившись поступательно на величину 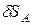влево (рис.15.5.).
Рис15.4 Расчетная схема
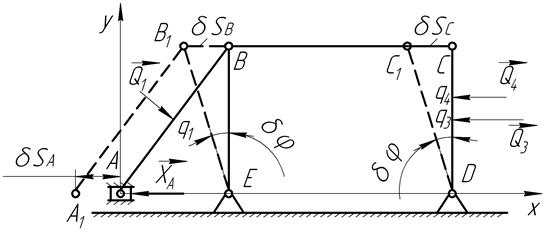
Рис.15.5
Звено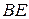 
займет положение 
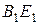, повернувшись на угол 
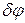относительно точки 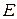, звено 
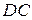- положение 
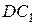. Угол его поворота, очевидно, равен углу поворота 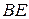. Вследствие полости угла поворота 
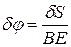вертикальным перемещением звена 
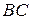можно пренебречь. Согласно вышесказанному запишем уравнение работ, выражающее принцип возможных перемещений:
;
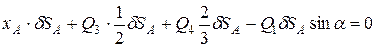откуда:
.
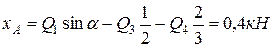Для определения вертикальной составляющей заменим мысленно цилиндрический шарнир 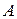ползуном, дающим возможность вертикального перемещения точки 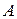(рис.14.6).
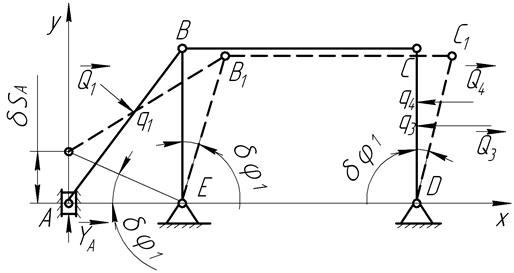
Рис.14.6
Придадим системе возможное перемещение 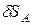под действием реакции . Тогда звено будет находиться в плоском движении 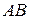с мгновенным центром вращения в точке 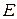и повернется на угол 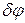, звенья 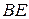и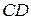 
повернутся относительно соответственно шарниров 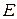и 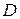на одинаковый угол 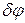,, а вертикальным перемещением звена можно пренебречь. Запишем уравнение работ:
.
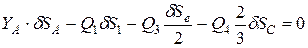Выразим возможные перемещения точек приложения сил через 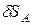. угол поворота звена 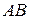вокруг точки :
;
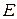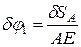где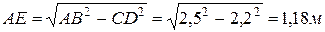 
.
Возможное перемещение точки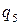 
:
,
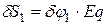где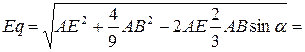 
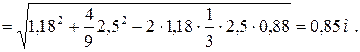
Возможное перемещение точки С:
.
Подставим найденные величины:
.
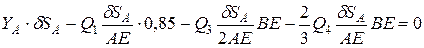Откуда:
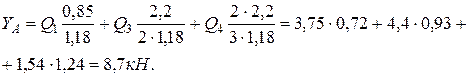
Реакция в шарнире также может быть разложена на две составляющие 
, 
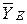. Произведем с шарниром 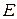те же преобразования, что и для шарнира 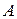. Для расчетной схемы с горизонтальным ползуном (рис.7), которая предполагает поступательное перемещение звеньев 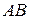, 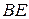и 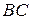влево на величину 
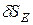и поворот звена 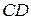относительно шарнира 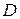на угол 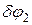, получим следующее уравнение работ:
Откуда:
.
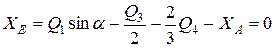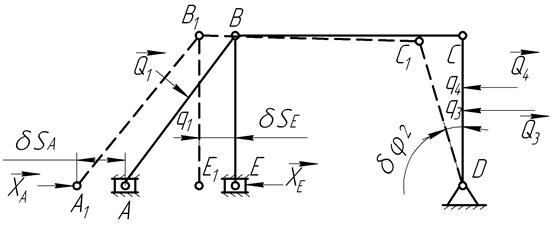
Рис.14.7
Для определения горизонтальной составляющей реакции в опоре 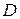мысленно заменим шарнир горизонтальным ползуном (рис.14.8).
Рис.14.8
Мгновенный центр вращения звена 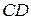находится в точке 
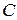, следовательно, данная схема предполагает только движение одного звена системы: поворот звена 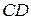вокруг точки 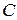на угол 
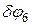. Составим уравнение работ, придав системе возможное перемещение в точке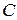 
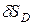:откуда:
.
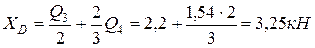Заменим мысленно шарнир в точке на вертикальный ползун и придадим системе возможное перемещение в направлении составляющей реакции 
(рис.14.9).
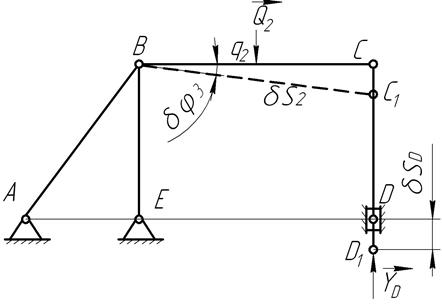
Рис.14.9
В этом случае, звено повернется на угол относительно точки 
, а звено 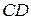опустится вертикально вниз на величину 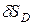, причем будет соблюдено соотношение:
.
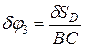Запишем уравнение работ:
;
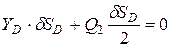откуда:
.
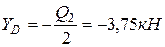Реакция направлена в противоположную сторону.
Для определения вертикальной составляющей реакции 
воспользуемся расчетной схемой, представленной на рис.14.10.
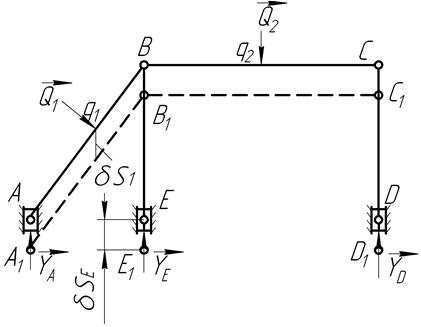
Рис.14.10
Заменив шарниры , , 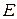вертикальными ползунами и добавив соответственно реакци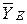и , и 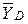придадим системе возможное перемещение в вертикальном направлении 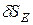. В этом случае все звенья системы переместятся поступательно на эту величину. Уравнение работ будет иметь вид:
;
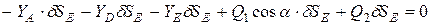откуда:
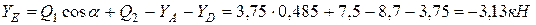
Таким образом, определены все составляющие реакций в опорах , , 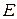. Произведем проверку решения, для этого составим для уравнения равновесия сил:
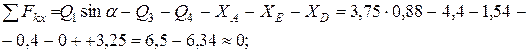
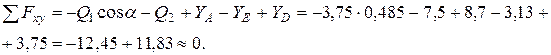
Довольно значительные расхождения обусловлены некоторыми допущениями, принятыми при решении.