Смешанные стратегии в антагонистических играх

Задачи теории игр

2.4.2.1. Оптимальные стратегии.

Рассмотрим игру с платежной матрицей.

	В1	В2	В3
А1		-4
А2	-3		-2

 

Предположим, что игра проводится многократно. Нам требуется выработать правильную линию поведения, обеспечивающую максимально возможный выигрыш.

Чтобы понять, как выработать правильную линию поведения, посмотрим, как вести себя не следует.

Выберем такую стратегию: будем каждый раз выбирать ход А₁. Противник быстро уловит это и будет отвечать нам ходом В₂. И тогда в каждой партии мы будем проигрывать 4 очка. Сменим стратегию. Будем аккуратно чередовать ходы: A₁, A₂, A₁, А₂,.... Наш противник быстро уловит и эту систему чередования и в ответ будет чередовать свои ходы так: В₂, В₁, В₂, В₁,..., а хода В₃ вообще делать не будет. Тогда в каждой нечетной партии мы выигрываем -4 очка, в каждой четной выигрыш составляет -3. Наш средний выигрыш -3,5. Фактически при такой стратегии в среднем мы проигрываем 3,5 очка, и чем дольше мы так глупо играем, тем больше проиграем. Пока наши стратегии неудачны, и понятно, что если мы заранее придумаем какой-нибудь другой план закономерного чередования ходов, то через несколько ходов наш противник разгадает этот план и ответит нам самым невыгодным для нас образом.

Изменим свою линию поведения принципиально. Будем чередовать ходы A₁ и А₂ с той же частотой, что и в предыдущем случае, но случайным образом: например, будем бросать монету перед каждым ходом, если выпадет герб, выберем ход A₁, если цифра, - А₂. Тогда вероятности первого и второго ходов равны числам 0,5 и 0,5. Пару чисел (0,5; 0,5) и назовем своей выбранной стратегией. Предположим, наш противник, посмотрев на нас, тоже стал бросать монету и при выпадении герба выбирать В₁, а при выпадении цифры — В₂. Хода В₃ он вообще решил не делать. Тогда его стратегия - вероятности ходов В₁,В₂, В₃ - есть тройка (0,5; 0,5; 0).

Посчитаем свой средний (ожидаемый) выигрыш. Вероятность получения 3 очков (при ходах А_1, В₁) есть Р(А₁,В₂) = Р(А₁)Р(В₁) = 0,25. (Мы использовали формулу вычисления вероятности произведения независимых событий.) Аналогично посчитаем вероятности каждого из остальных пяти выигрышей.

aij		-4		-3		-2
P(aij)	0,25	0,25		0,25	0,25

 

Средний выигрыш при заданной паре стратегий равен математическому ожиданию случайной величины а_ij

M(а_ij) = 3×0,25 - 4×0,25 + 0 - 3×0,25 + 2×0,25+0 = -0,5.

Ну что ж, при нашей стратегии (0,5; 0,5) и ответной стратегии противника (0,5; 0,5; 0) наш выигрыш больше, чем при предыдущих стратегиях. А вот наш противник предпочел бы, чтобы мы, как и раньше, чередовали ходы аккуратно. Понимая, что к прежней линии поведения мы уже не вернемся, он должен подумать, не стоит ли ему чередовать свои ходы, разумеется, случайно (иначе мы разгадаем его планы и увеличим свой выигрыш), но с другими частотами. Например, так: (0,33; 0,33; 0,33) или так: (0,5; 0,25; 0,25). Для каждой его стратегии и нашей стратегии (0,5;0,5) он подсчитает выигрыш и выберет лучшую. Но тогда и мы постараемся выбрать более выгодную для нас стратегию. И если это у нас получится, наш противник снова будет вынужден пересматривать свои стратегии в поисках более выгодной.

Будет ли конец нашим метаниям? Да, будет, если мы грамотно воспользуемся методами теории игр. В теории игр доказано, что есть такая пара стратегий, их называют оптимальными, что ни одному игроку невыгодно отклоняться от своей оптимальной, если другой игрок придерживается своей оптимальной стратегии. Рассмотрим понятие оптимальной стратегии более подробно.

Пусть игра имеет платежную матрицу в т строк и п столбцов. Стратегией первого игрока назовем любую последовательность неотрицательных чисел Р=(p_1,p₂,...,p_m,), такую, что р₁+р₂+...+р_m = 1, а стратегией второго игрока последовательность также неотрицательных чисел Q = (q₁,q₂,..,q_n), такую, что q₁ + q₂ +...+ q_n = 1. Выигрыш при многократном проведении игры зависит от пары выбранных стратегий. Если игрок делает все время один и тот же ход, то такая стратегия называется чистой, в противном случае стратегия называется смешанной. Обозначим Е = (Р,Q) выигрыш игрока А при выборе игроками стратегий Р, Q.

Пусть Р*, Q* некоторая пара стратегий игроков А и В, v — некоторое число. Пусть для любых стратегий Р, Q выполняется неравенство:

E(P, Q*)≤v≤ E(P*, Q)

Тогда стратегии Р* и Q* называются оптимальными, а число v — ценой игры.

Во-первых, отметим, что выписанные выше неравенства выполняются для любых Р и Q, в том числе и для Р* и Q*:

Е (Р*, Q*)≤v≤Е (Р*, Q*)

следовательно,

Е(Р*,Q*) = v

Таким образом, цена игры — это тот средний выигрыш первого игрока, который получается, если игроки применяют свои оптимальные стратегии.

Предположим, игрок А решил уклониться от своей оптимальной стратегии и применил другую, а именно, стратегию Р, а игрок В применяет оптимальную. Тогда игрок А получит меньший выигрыш, чем мог бы, применяя оптимальную стратегию. Действительно,

v₁ = Е(Р, Q*)≤v.

Значит, первому игроку невыгодно уклоняться от оптимальной стратегии, если второй применяет оптимальную.

Пусть теперь игрок В выбрал не оптимальную стратегию Q, (а игрок А применяет оптимальную). Оценим выигрыш А:

v₂ = Е(Р*, Q)≥ v.

В этом случае игрок В позволит игроку А получить больший выигрыш, чем он мог бы получить, если бы В не уклонялся от оптимальной стратегии. Значит, игроку В также невыгодно уклоняться от своей оптимальной стратегии, пока А применяет оптимальную.

Итак, ни одному из игроков невыгодно уклоняться от оптимальной стратегии, если другой применяет стратегию оптимальную.

Решением игры называется совокупность трех величин: двух оптимальных стратегий Р*,Q* и цены игры v.

 

2.4.2.2. Нахождение решения игры

Возникают два естественных вопроса. Во-первых, как найти оптимальные стратегии? Во-вторых, если они найдены, то, как ими воспользоваться? Ведь оптимальная стратегия — это всего лишь последовательность чисел, а игроку надо делать ходы.

Второй вопрос решить легко. Если бы мы знали свою оптимальную стратегию, мы бы придумали, как ее реализовать. Например, если бы она представляла собой пару (0,5; 0,5), то мы перед каждым ходом могли бы бросать монету и при выпадении герба выбирали бы первый ход, а при выпадении цифры — второй. Стратегию (, ) можно было бы реализовать бросанием кости: при выпадении 1 или 2 выбирать первый ход, в остальных случаях — второй. Для оптимальной стратегии (, ) мы написали бы пять записок – на двух из них число 1 (первый ход) на трех – число 2 (второй ход), и перед каждым ходом устраивали бы жеребьевку. Короче говоря, мы сумеем воспользоваться оптимальной стратегией, если найдем ее. Но как найти оптимальную стратегию?

Мы подошли к вопросу о нахождении решения игры.

Пусть платежная матрица имеет вид

	B1	B2	...	Bn
A1	a11	a21	...	a1n
A2	a21	a22	...	a2n
...	...	...	...	...
Am	am1	am2	...	amn

 

Будем считать, что все a_ij ≥0. Если это не так, то добьемся того, чтобы все элементы матрицы стали неотрицательными. Для этого достаточно прибавить к каждому элементу матрицы некоторое число (одно и то же для всех элементов). При этом цена игры увеличится на это же самое число, а оптимальные стратегии не изменятся (этот факт доказан в теории игр). Итак, считаем, что все элементы платежной матрицы неотрицательны. Обозначим Р*= (Р_1,Р₂, …, Р_m), Q*= (Q₁,Q₂,..., Q_n), — оптимальные стратегии, v — цена игры (эти величины и надо найти). По определению стратегий

р₁+р₂+...+р_m = 1,

q₁+q₂+...+q_n = 1

Пусть наш противник В сделал ход В₁. Посчитаем наш ожидаемый выигрыш, если будем пользоваться оптимальной стратегией. Он равен

а₁₁р₁+ а₂₁p₂ +…+ а_m1p_m,

и он должен быть не меньше цены игры v, ведь мы применяем оптимальную стратегию. Аналогично посчитаем ожидаемые выигрыши для тех оставшихся случаев, когда противник делает другие ходы, а мы - ходы, соответствующие нашей оптимальной стратегии. И каждый раз наш ожидаемый выигрыш не меньше v.

Мы получаем систему неравенств:

а₁₁р₁+ а₂₁p₂ +…+ а_m1p_m ≥ v

а₁₂р₁+ а₂₂p₂ +…+ а_m2p_m ≥ v

_{.....................................................}

а_1nр₁+ а_2np₂ +…+ а_mnp_m ≥ v

В этой системе разделим все неравенства на положительное число v и введем обозначения: 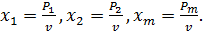Получим систему:

а₁₁x₁+ а₂₁x₂ +…+ а_m1x_m ≥1

а₁₂x₁+ а₂₂x₂ +…+ а_m2x_m ≥1

_{.....................................................}

а_1nx₁+ а_2nx₂ +…+ а_mnx_m ≥1

При этом, так как p₁+p₂+…+p_m=1, то 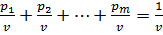, т.е. x₁+x₂+…+x_m= . Мы ищем свою оптимальную стратегию, т.е. ту, которая максимизирует наш выигрыш 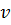. Но при максимальном значении 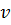величина принимает минимальное значение.

Итак, нашу задачу мы свели к следующей: найти неотрицательное решение системы (1), на которой функция f = x₁+x₂+…+x_m принимает минимальное значение. Мы получаем задачу линейного программирования, а методы решения таких задач известны.

Для нахождения оптимальной стратегии противника мы аналогичным образом (не забывая о том, что ему надо минимизировать наш выигрыш) получаем задачу вида: максимизировать функцию g=y₁+y₂+…+y_n (y_j= )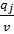

на множестве неотрицательных решений системы неравенств:

 

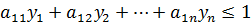
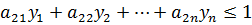
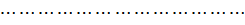
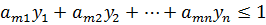
Эта и предыдущая задачи – двойственные задачи линейного программирования. Отметим без доказательства, что они имеют решения и minf=maxg. Следовательно, пара оптимальных стратегий существует, и существует цена игры. Таким образом, для любой конечной матричной игры существует решение и его можно найти методами линейного программирования.

Выше мы рассмотрели игру с платежной матрицей, заданной таблицей

	В1	В2	В3
А1		-4
А2	-3		-2

 

Решим эту игру. К каждому элементу этой матрицы прибавим 4, тогда цена игры тоже увеличится на 4. Получим матрицу

	В1	В2	В3
А1
А2

Сначала решим игру с этой матрицей. Составим две двойственные задачи.

а) Минимизировать функцию

f=x₁+x₂

на множестве неотрицательных решений системы:

7x₁+x₂ ≥ 1

6x₂ ≥ 1

4x₁+2x₂ ≥ 1

 

б) Максимизировать функцию

g=y₁+y₂+y₃

на множестве неотрицательных решений системы:

7y₁+4y₃≤1

y₁+6y₂+2y₃≤1

Первую из них можно решить графически (рис.1). На рис. 1 прямые (1), (2), (3) заданы уравнениями 7x₁+x₂ =1, 6x₂ = 1, 4x₁+2x₂ =1.

Найдем точки пересечения границ задающих область всех решений системы ограничений. Все точки системы ограничений лежат выше оси OX₁ (6x₁≥1) Границы системы ограничений этой задачи пересекают ось OX₂, в точках (0,1), 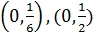. Из них только первая находится в области ограничений, обозначим ее M.

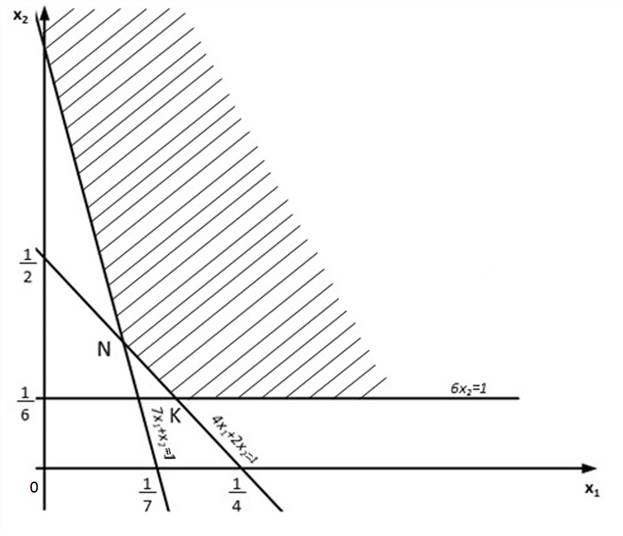
Рис. 1.

 

Найдем остальные точки пересечения границ. Для этого решим три системы уравнений:

7x₁+x₂ = 1

6x₂ = 1

 

7x₁+x₂ = 1

4x₁+2x₂ = 1

 

6x₂ = 1

4x₁+2x₂ = 1

 

Первая из них имеет решение 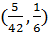, вторая - 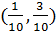, третья - 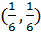. Первая из этих точек не входит в область ограничений (она не удовлетворяет неравенству 4x₁+2x₂ ≥ 1), две другие – входят. Обозначим их , .

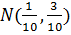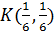Выясним, какая из точек: M, N или K, - дает минимальное значение f.

f (M)=0+1+1,

f(N)= ,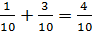

f(K)=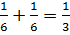

Таким образом, minf= и достигается он при .

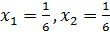Так как 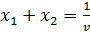, то цена игры равна 3, а, следовательно, цена игры для первоначальной задачи равна -1 (мы прибавляли ко всем платежам матрицы число 4).

Теперь, используя обозначения 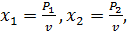находим пару (p₁, p₂)

x₁ = vp ₁= , x₂ = vp₂= .

Следовательно, оптимальной стратегией игрока А является пара чисел .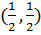

Теперь найдем оптимальный план для задачи б). Добавим неотрицательные неизвестные y₄ и y₅ и получим каноническую систему ограничений:

7y₁+4y₃+y₄=1

y₁+6y₂+2y₃+y₅= 1

 

Постоим симплексную таблицу для этой задачи.

Из таблицы мы видим, что maxg = , оптимальный план .

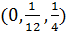Следовательно, оптимальной стратегией второго игрока является тройка , а цена игры равна v = 3–4 = -1, что подтверждается решением первой из этих двойственных задач.

 

Цены	Базис	Свободные коэффициенты	цены
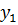
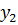
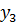
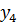
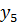
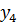
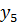
			-1	-1	-1
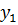
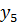
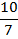
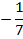
				-1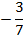
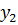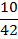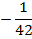
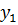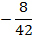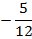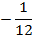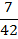