Задачи теории игр
2.4.1.1. Основные понятия теории игр
В реальной жизни возникают ситуации, когда две или несколько сторон с несовпадающими, а иногда и противоположными, интересами решают общую проблему. В подобных ситуациях каждая сторона производит какое-то действие, выгодное, с ее точки зрения, для нее самой. Однако результат его зависит не только от действия данной стороны, но и от линии поведения всех остальных сторон. Такие ситуации называются конфликтными ситуациями. Часто конфликтные ситуации возникают в экономике (особенно в условиях конкуренции), в ходе военных действий, в политике. Столкновение противоречащих друг другу интересов наблюдается в судопроизводстве, в спорте, в предвыборной борьбе.
Необходимость анализировать конфликтные ситуации привела к возникновению специальной математической теории — теории игр. Теорию игр можно считать математической теорией конфликтных ситуаций. Цель ее — выработка рекомендаций по разумному поведению участников конфликта.
Каждая жизненная конфликтная ситуация очень сложна, учесть все факторы, влияющие на ее исход, чрезвычайно трудно. Чтобы сделать возможным математический анализ конфликтной ситуации, необходимо отвлечься от второстепенных факторов и построить упрощенную модель ситуации. Математическая модель конфликтной ситуации называется игрой.
Всем известны такие формализованные модели конфликтных ситуаций, которые в буквальном смысле слова являются играми: шашки, шахматы, домино, лото, карточные игры. Именно от них математическая теория игр взяла свое название и терминологию: стороны, участвующие в конфликтной ситуации, именуются игроками, их действия — ходами, а результат столкновения — выигрышем каждой из сторон.
Если в игре сталкиваются интересы двух противников, то игра называется парной, если противников больше, чем два, — множественной. В теории игр наиболее глубоко разработано направление, посвященное анализу парных игр. Здесь мы ограничимся рассмотрением таких конфликтных ситуаций, которые можно свести к парным играм.
Будем рассматривать парную игру с двумя игроками А и В.. Сторону А для удобства будем называть «мы», сторону В — «противник.
Результат игры, выигрыш или проигрыш для каждого из игроков, не всегда имеет количественное выражение, но, как правило, для него можно подобрать числовую характеристику.
Если сумма выигрышей всех игроков равна 0, то игра называется игрой с нулевой суммой. Любая карточная игра «на деньги» с любым числом участников является игрой с нулевой суммой. Очевидно, что в парной игре с нулевой суммой один игрок выигрывает то, что проигрывает другой. Если в парной игре с нулевой суммой стороны представляют противоположные интересы, т. е. каждый игрок заинтересован только в увеличении своего собственного выигрыша, то игра называется антагонистической. Если выигрышу и проигрышу игроков приписать значения 1 и -1, соответственно, а в случае «ничьей» — игрокам приписать по 0, то игру в шахматы можно считать антагонистической.
Одним из основных понятий в теории игр является понятие платежной матрицы. Рассмотрим его на следующих примерах.
Пример 1. Каждый из двух игроков А и В одновременно и независимо друг от друга записывает одно из чисел 1 или 2. Если сумма записанных чисел четна, то второй игрок платит первому рубль, если нечетна, то первый платит рубль второму.
У каждого из игроков по два хода. Предположим, игрок А построил таблицу своих выигрышей – зависимость выигрыша от выбора своего хода и выбора хода противника.
| В1 | В2 | |
| А1 | -1 | |
| А2 | -1 |
Очевидно, что у игрока В таблица выигрышей имеет вид:
| В1 | В2 | |
| А1 | -1 | |
| А2 | -1 |
Соответствующие элементы этих двух таблиц отличаются только знаком, а значит, для анализа игры достаточно иметь одну из них. В теории игр принято анализировать игру по таблице выигрышей игрока А. Эту таблицу называют платежной матрицей игры.
Пример 2.Каждый из двух игроков одновременно называет одну из сторон монеты (герб, цифра) либо молчит. Если оба игрока сделали один и тот же ход, то игрок А платит игроку В два рубля, если же их ходы различны, то А получает от В один рубль.
Платежная матрица имеет вид:
| В1 (г) | В2 (ц) | В3 (м) | |
| А1 (г) | -2 | ||
| А2 (ц) | -2 | ||
| А3 (м) | -2 |
Пример 3. Пусть в нашем распоряжении имеется три вида вооружения A1, A2, A3, у противника — три вида самолетов В1 , В2, В3. Наша задача — поразить самолет, задача противника — сохранить его непораженным. При применении оружия A1 самолеты В1, В2, В3 поражаются с вероятностями 0,9, 0,4 и 0,2, соответственно, при применении А 2— с вероятностями 0,3, 0,6 и 0,8, при применении A3 — с вероятностями 0,5, 0,7 и 0,2. Построим математическую модель ситуации.
У нас три хода — три варианта выбора вооружения — A1, A2, A3. У противника также три хода - выбор самолета В1, В2, В3. Наш выигрыш равен 1,
если самолет поражен, и 0, если он не поражен. Однако определить точное значение выигрыша при выборе нашего хода и хода противника нельзя - самолет поражается лишь с определенной вероятностью, и выигрыш - величина случайная. Здесь мы должны принять в качестве числового значения выигрыша его математическое ожидание - в данном случае - его вероятность. Тогда платежная матрица выглядит так:
| В1 | В2 | В3 | |
| А1 | 0,9 | 0,4 | 0,2 |
| А2 | 0,3 | 0,6 | 0,8 |
| А3 | 0,5 | 0,7 | 0,2 |
Как разумно вести себя в каждой из этих ситуаций? Об этом и пойдет сейчас речь.
Основной целью теории игр является выработка правильной линии поведения каждой из сторон в конфликтной ситуации. Что понимается под словами «правильная линия поведения»? Правильная линия поведения должна обеспечить игроку максимально возможный выигрыш. Всегда ли она существует? Нет, не всегда. Представим, что мы вдвоем играем в такую игру: по очереди кладем на круглый стол пятаки, не накрывая один другим даже частично. Проигрывает тот, кто уже не может положить пятак, потому что на столе нет для него места. Предположим, первый ход делает наш противник. Тогда у нас заведомо проигрышная ситуация. Действительно, наш противник положит первый пятак точно в центр стола, а затем будет делать ходы, симметричные нашим относительно центра. Очевидно, что при такой его стратегии выигрыш ему обеспечен, как бы мы ни старались. Таких игр много, но играть в них есть смысл только тем, кто не догадывается, в чем тут дело. Мы не будем говорить о подобных играх.
Теория игр, как и всякая математическая теория, имеет свои ограничения. Одним из них является предположение о полной разумности противника (противников). В реальном конфликте зачастую оптимальная стратегия состоит в том, чтобы угадать, в чем противник глуп, и воспользоваться этой глупостью в свою пользу. Теория игр исключает такое поведение. Кроме того, схемы теории игр исключают элементы риска, которые в реальных конфликтах неизбежны даже при разумной линии поведения. В теории игр выявляется наиболее осторожное, «перестраховочное» поведение участников конфликта.
2.4.1.2 Принцип минимакса
Рассмотрим антагонистическую игру с платежной матрицей, заданной таблицей.
| B1 | B2 | B3 | B4 | B5 | |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 |
В матрице есть клетка с выигрышем 12. Чтобы получить его, надо выбрать ход A 3. Но ведь наш разумный противник должен понимать, что мы польстимся на этот выигрыш, а значит, он должен ответить нам ходом B 3. И тогда вместо предполагаемого выигрыша 12 мы получим лишь выигрыш 1. Нет, мы не можем так рисковать. Какой же ход выбрать? Исходя из принципа осторожности, мы должны выбрать тот ход, при котором наш минимальный выигрыш будет максимальным. Как же его выбрать? Для каждого нашего хода найдем самый неудачный, самый маленький выигрыш. Легко видеть, что для хода A 1, самым плохим выигрышем является 4 (это - минимальное число первой строки) для A 2– это число 2, для A 3 - 1, для A 4 - 5. Выпишем эти числа в дополнительный столбец платежной матрицы, обозначим их a i:
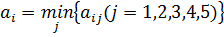
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| bj |
Максимальное из чисел a i равно 5, и оно соответствует ходу A 4. Если мы выберем этот ход, то самое малое, что мы можем получить, это 5. При других вариантах мы рискуем получить меньше.
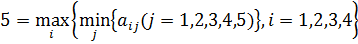
Выигрыш 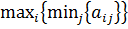 , в нашем случае это 5, называется нижней ценой игры или максимином, а ход игрока A, ему соответствующий – максиминной стратегией. Максимин – наш гарантированный выигрыш. Если мы поведем себя осторожно, то меньше 5 не получим.
, в нашем случае это 5, называется нижней ценой игры или максимином, а ход игрока A, ему соответствующий – максиминной стратегией. Максимин – наш гарантированный выигрыш. Если мы поведем себя осторожно, то меньше 5 не получим.
Теперь встанем на позицию нашего противника. Как он должен рассуждать? Ему бы хотелось, чтобы мы взяли самый маленький выигрыш, а именно, 1. Для этого ему необходимо сделать ход B 3. Но этого недостаточно. Мы ведь можем разгадать его замысел, ответив ему ходом A1, и взять выигрыш 7. Понимая это, игрок B остережется этого хода. Вообще он, как и мы, попробует перестраховаться: из самых плохих исходов он выберет лучший. Самыми плохими для него исходами при ходах B 1, B 2, B 3, B 4, B 5 являются наши выигрыши 12, 10, 7, 9, 10. Это максимальные числа столбцов, обозначим их bj:
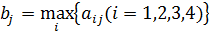
Припишем эти числа в дополнительную строку платежной матрицы. Самым лучшим для B из этих исходов является минимальное из этих чисел, это число 7:
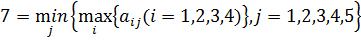
Это число соответствует стратегии B 3, оно называется верхней ценой игры или минимаксом, а ход игрока B, ему соответствующий – минимаксной стратегией. Если игрок B будет вести себя осторожно, то больше 7 очков он нам не отдаст.
Итак, если оба игрока соблюдают принцип осторожности, то они выберут ходы, соответствующие максимину и минимаксу. В теории игр эта пара стратегия называется минимаксной парой, а выбор этой пары называется принципом минимакса. Принцип минимакса рекомендует следующую линию поведения: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш (минимальный проигрыш). Для данного примера минимаксные стратегии - A 4, B 3, при использовании их обоими игроками игрок A получает выигрыш 5 очков.
Вернемся к примерам, рассмотренным в начале лекции. Легко видеть, что в каждой из игр первых двух примеров любая пара ходов является минимаксной. Поэтому если они проводятся только по одному разу, нет смысла рассуждать, какой ход сделать, можно выбрать любой.
Теперь рассмотрим задачу о поражении самолетов (пример 3) и по принципу минимакса найдем пару минимаксных стратегий.
| B1 | B2 | B3 | min ai | |
| A1 | 0,9 | 0,4 | 0,2 | 0,2 |
| A2 | 0,3 | 0,6 | 0,8 | 0,3 |
| A3 | 0,5 | 0,7 | 0,2 | 0,2 |
| max aj | 0,9 | 0,7 | 0,8 |
Нижняя цена игры 0,3. Если мы воспользуемся вооружением A 2, то поразим самолет противника с вероятностью, не менее, чем 0,3. Наиболее осторожной стратегией противника является использование самолета B 2; применяя его, противник может рассчитывать, что его самолет будет поражен с вероятностью не более, чем 0,7. Здесь можно спрогнозировать результат ситуации: с вероятностью 0,6 самолет противника будет поражен.
2.4.1.3.Игра с седловой точкой
Рассмотрим игру с платежной матрицей, заданной таблицей:
| B1 | B2 | B3 | B4 | |
| A1 | ||||
| A2 | ||||
| A3 |
Пара минимаксных стратегий - A2, B2. В этой игре нижняя цена игры равна верхней цене и равна 6. Предположим, мы узнали, что наш противник выбрал минимаксную стратегию В2. Стоит ли нам уклоняться от своей максиминной? Нет, не стоит. Максиминная стратегия дает нам выигрыш 6, а любая другая - меньший. Итак, выбираем ход А2. Предположим, наш противник узнал об этом. Изменит ли он свое решение? Любой другой его ход устраивает нас больше, чем В2. Именно поэтому наш противник остановится на ходе В2. Итак, в данной ситуации любое (одностороннее) отступление от принципа минимакса ведет к потерям отступившей стороны, и в этом смысле минимаксные стратегии устойчивы. Такая ситуация возможна только в тех играх, где верхняя цена игры равна нижней. В этом случае верхняя и нижняя цена игры называется просто ценой игры, или седловой точкой. В играх с седловой точкой решением игры называется пара минимaксных стратегий, эти стратегии и являются оптимальными.