Вычисление объемов тел по известным поперечным сечениям.Пусть дано тело 
, ограниченное замкнутой поверхностью. И пусть известна площадь любого его сечения плоскостью, перпендикулярной к оси абсцисс (рис.9, а,б). Эти сечения называются поперечными. Положение поперечного сечения определяется абсциссой точки его пересечения с осью 
.
С изменением 
площадь 
поперечного сечения изменяется, т.е. является некоторой функцией от . Обозначим ее 
. Функцию будем считать непрерывной на отрезке 
, где 
и 
– абсциссы крайних сечений тела .
Рис.9.Объем пространственного тела
Теорема 5. Объем тела, заключенного между двумя плоскостями 
и 
, в случае, если площадь сечения, проведенная перпендикулярно к оси Ох, есть известная функция от , 
, вычисляется по формуле
.
► Для вычисления объема 
тела применяется алгоритм составления интегральной суммы и предельного перехода к определенному интегралу.
1. Разобьем отрезок 
на 
частичных отрезков точками
.
Обозначим 
, 
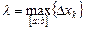
. Через точки разбиения 
, проведем плоскости, перпендикулярные к оси Ох. Семейство плоскостей 
, , разобьет данное тело на слои, толщина каждого из которых равна 
, .
2. На каждом из частичных отрезков 
, , выберем произвольным образом точку 
и найдем значения 
функции в этих точках.
3. Предположим, что на каждом из частичных отрезков функция постоянна и совпадает со значением . Тогда каждый слой тела представляет собой прямой цилиндр с основанием 
и образующими, параллельными оси Ох. Объем такого частичного прямого цилиндра вычисляется по формуле
.
где 
– высота частичного цилиндра.
Объем 
всего тела 
приближенно равен объему фигуры, состоящей из 
ступенчатых частичных цилиндров (см. рис.10, б):
.
Очевидно, что последнее приближенное равенство тем точнее, чем меньше диаметр разбиения отрезка 
.
4. За точное значение искомого объема примем
.
Заметим, что сумма 
является интегральной суммой для непрерывной функции на отрезке . Следовательно,
.◄
Пример. Вычислить объем тела, ограниченного эллипсоидом 
.
Решение. Пересечем эллипсоид плоскостью 
. В сечении получим эллипс 
Площадь поперечного сечения равна 
.
Тогда 
.
Вычисление объемов тел вращения.Рассмотрим тело, образованное вращением вокруг оси 
криволинейной трапеции 
, ограниченной кривой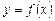 
, осью Ох и прямыми 
, 
(рис.10).
Рис.10. Объем тела вращения около оси 
| 
Рис.11. Объем тела вращения около оси 
|
Если пересечь это тело плоскостями, перпендикулярными к оси Ох, получим круги, радиусы которых равны модулю ординат 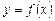точек данной кривой. Следовательно, площадь сечения рассматриваемого тела
.
Применяя формулу 
, получаем формулу для вычисления объема тела вращения
.
Если тело образовано вращением вокруг оси 
криволинейной трапеции 
(рис.11), то его объем вычисляется по формуле
,
где 
, 
, – уравнение кривой 
.
Пример. Вычислить объем тела, получающегося от вращения вокруг оси одной арки синусоиды 
.
Решение. Имеем
.
Вопросы для самоконтроля
1. По каким формулам вычисляются площади криволинейных трапеций, ограниченных линиями, заданными в декартовой системе координат, в параметрическом виде и в полярной системе координат?
2. Приведите формулы для вычисления длин дуги кривой, заданной в декартовой системе координат, в параметрическом виде и в полярной системе координат?
3. Как вычислить площадь поверхности тела?
4. Как вычисляется объем пространственных тел?