Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Владимирский Государственный Университет
Имени Александра Григорьевича и Николая Григорьевича Столетовых»
Институт Экономики и Менеджмента
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Инвестиции»
Вариант № 4
Выполнил:
ст. гр. ЗЭКсд-114
Кукушкина О.А.
Принял: к.э.н.,
Марченко Е.М.
Владимир 2016
Задача №1.
Определить срок в годах, при начислении простых процентов, по следующим данным:.
| Вариант | ||||||||||
| Процентная ставка | ||||||||||
| Вклад, тыс. руб. | ||||||||||
| Вклад с процентами |
Решение
Используя формулу: 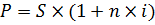 , где
, где
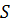 – вклад,1500
– вклад,1500
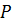 - вклад с процентами,7600
- вклад с процентами,7600
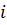 - процентная ставка,16
- процентная ставка,16
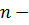 срок в годах.?
срок в годах.?
7600=1500x(1+16n/100)
7600=1500+240n
6100=240n=>n=6100/240=25 5/12
Ответ: срок в годах 25 лет 5 месяцев
Задача №2.
Рассчитать сумму начисленных % (сложные %).
| Вариант | ||||||||||
| Период | ||||||||||
| Годовая процентная ставка | ||||||||||
| Капитализация | Ежеквартальная | Полугодовая | Ежеквартальная | Полугодовая | Ежеквартальная | Полугодовая | Ежеквартальная | Полугодовая | Ежеквартальная | Полугодовая |
| Вклад |
Решение
Определяем сумма вклада с начисленными процентами по формуле:
S=P(1+j/m)mn
Где 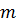 - количество начислений в течение года,
- количество начислений в течение года,
 – номинальная процентная ставка, т.е. годовая процентная ставка при m начислениях в году.
– номинальная процентная ставка, т.е. годовая процентная ставка при m начислениях в году.
S=5000(1+20/200) 8 =5000(1+0.1) 8 =11789.74
Рассчитаем сумму начисленных процентов:
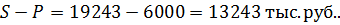
S-P= 11789.74-5000=6789.74
Ответ: Сумма начисленных процентов составила 6789,74 т.руб.
Задача №3.
На депозитный счет в течение ряда лет будут в конце каждого квартала вноситься суммы, на которые будут начисляться сложные проценты. Определить сумму %, которую банк выплатит владельцу счета по следующим данным:
| Вариант | ||||||||||
| Период, лет | ||||||||||
| Годовая процентная ставка,% | ||||||||||
| Капитализация | ежеквартальная | |||||||||
| Платеж, тыс. руб. |
Решение: m*n
S= 300*(1+j/m) -1
r/m
4*3
S= 300(1+0.2/4) - 1 =
0.2/4
= 10755.2 тыс.руб.
Ответ: 10755.2 тыс.руб.
Задача №4.
Рассчитайте показатели чистого дисконтированного дохода, рентабельности инвестиций и внутреннюю норму окупаемости по следующим данным:
| Вариант проекта | Денежные потоки по годам, тыс. руб. | |||||
| 0‑й | 1‑й | 2‑й | 3‑й | 4‑й | 5‑й | |
| А | -50 | 15,5 | 15,5 | 15,5 | 15,5 | 15,5 |
| Б | -80 |
Выберите эффективный вариант проекта при r равной:.
| Вариант | ||||||||||
| Годовая процентная ставка |
Решение:
| период | Денежный поток А | Коэффициент дисконтирования, при i=16% | NPV1 |
| -50 | -50 | ||
| 15,5 | 0,8621 | 13,4 | |
| 15,5 | 0,7432 | 11,5 | |
| 15,5 | 0,6406 | 9,9 | |
| 15,5 | 0,5523 | 8,6 | |
| 15,5 | 0,4761 | 7,4 | |
| период | Денежный поток Б | Коэффициент дисконтирования, при i=16% | NPV2 |
| -80 | -80 | ||
| 0,8621 | 17,2 | ||
| 0,7432 | 7,4 | ||
| 0,6406 | 9,6 | ||
| 0,5523 | 16,6 | ||
| 0,4761 | 14,3 |
Коэффициент дисконтирования рассчитывается по формуле:
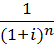
Находим чистый дисконтированный доход:
NPV1= -50+50,8= 0,8
NPV2=-80+65,1=-14,9
Эффективным считается проект А, так как NPV1 имеет положительное значение, а NPV2 – отрицательное.
Можно рассчитать срок окупаемости:
PP= 4 + 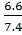 = 4,89 года
= 4,89 года
И рентабельность проекта:
PI = 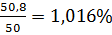
Внутреннюю норму окупаемости (дохода) рассчитываем следующим образом:
IRR =  +
+ 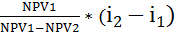
IRR = 16 +  = 16+0,051*32 » 17,6%
= 16+0,051*32 » 17,6%
Задача №5.
Пользуясь таблицей аннуитетов, определите дисконтированную и будущую стоимость денежных потоков по следующим данным:
| вариант | PV аннуитет | PV разница | FV аннуитет | FV разница | |
| Платежи по годам | |||||
| -200 | |||||
| -400 | |||||
| -400 | |||||
| -200 | |||||
| Годовая процентная ставка, % |
PVCF = 400 * 4,03 + 400 * 1 - 200 * 0,694 – 400 * 0,579 + 100 * 0,402 = 1681,80
FVCF = 400 * 20,8 + 400 * 1 + 100 * 5,37 – 400 * 9,93 - 200 * 12,92 = 2701
Задача №6.
Определить величину срочных разовых выплат по погашению кредита двумя способами: равными выплатами основного долга и равными платежами.
| Вариант | ||||||||||
| Величина кредита (тыс. руб.) | ||||||||||
| Сложная годовая процентная ставка | ||||||||||
| Период начисления процентов на неоплаченную часть долга | Ежегодно | Ежеквартально | Ежегодно | Ежеквартально | Ежегодно | Ежеквартально | Ежегодно | Ежеквартально | Ежегодно | Ежеквартально |
| Срок кредитования (лет) |
Величина срочных разовых выплат по погашению кредита равными выплатами основного долга:
Определим равные выплаты основного долга:

Расчеты величин срочных разовых выплат по погашению кредита равными выплатами основного долга представлены в таблице 1
Таблица 1
| Остаток на начало периода | погашение | остаток на конец | ||
| всего | в том числе | |||
| %-ты | основной долг | |||
| 95 000 | 92 031 | |||
| 89 062 | ||||
| 86 094 | ||||
| 83 125 | ||||
| 80 156 | ||||
| 77 187 | ||||
| 74 219 | ||||
| 71 250 | ||||
| 68 281 | ||||
| 65 312 | ||||
| 62 344 | ||||
| 59 375 | ||||
| 56 406 | ||||
| 53 437 | ||||
| 50 469 | ||||
| 47 500 | ||||
| 44 531 | ||||
| 41 562 | ||||
| 38 594 | ||||
| 35 625 | ||||
| 32 656 | ||||
| 29 687 | ||||
| 26 719 | ||||
| 23 750 | ||||
| 20 781 | ||||
| 17 813 | ||||
| 14 844 | ||||
| 11 875 | ||||
| 8 906 | ||||
| 5 937 | ||||
| 2 969 | ||||
Определить величину срочных разовых выплат по погашению кредита равными платежами.
R = 
| Остаток на начало периода | погашение | остаток на конец | ||
| всего | в том числе | |||
| %-ты | основной долг | |||
| 95 000,00 | 5 315,12 | 3 800,00 | 1 515,12 | 93 484,88 |
| 93 484,88 | 5 315,12 | 3 739,40 | 1 575,72 | 91 909,16 |
| 91 909,16 | 5 315,12 | 3 676,37 | 1 638,75 | 90 270,41 |
| 90 270,41 | 5 315,12 | 3 610,82 | 1 704,30 | 88 566,11 |
| 88 566,11 | 5 315,12 | 3 542,64 | 1 772,47 | 86 793,64 |
| 86 793,64 | 5 315,12 | 3 471,75 | 1 843,37 | 84 950,27 |
| 84 950,27 | 5 315,12 | 3 398,01 | 1 917,11 | 83 033,17 |
| 83 033,17 | 5 315,12 | 3 321,33 | 1 993,79 | 81 039,38 |
| 81 039,38 | 5 315,12 | 3 241,58 | 2 073,54 | 78 965,84 |
| 78 965,84 | 5 315,12 | 3 158,63 | 2 156,48 | 76 809,36 |
| 76 809,36 | 5 315,12 | 3 072,37 | 2 242,74 | 74 566,61 |
| 74 566,61 | 5 315,12 | 2 982,66 | 2 332,45 | 72 234,16 |
| 72 234,16 | 5 315,12 | 2 889,37 | 2 425,75 | 69 808,41 |
| 69 808,41 | 5 315,12 | 2 792,34 | 2 522,78 | 67 285,63 |
| 67 285,63 | 5 315,12 | 2 691,43 | 2 623,69 | 64 661,94 |
| 64 661,94 | 5 315,12 | 2 586,48 | 2 728,64 | 61 933,30 |
| 61 933,30 | 5 315,12 | 2 477,33 | 2 837,78 | 59 095,52 |
| 59 095,52 | 5 315,12 | 2 363,82 | 2 951,30 | 56 144,22 |
| 56 144,22 | 5 315,12 | 2 245,77 | 3 069,35 | 53 074,88 |
| 53 074,88 | 5 315,12 | 2 123,00 | 3 192,12 | 49 882,76 |
| 49 882,76 | 5 315,12 | 1 995,31 | 3 319,81 | 46 562,95 |
| 46 562,95 | 5 315,12 | 1 862,52 | 3 452,60 | 43 110,35 |
| 43 110,35 | 5 315,12 | 1 724,41 | 3 590,70 | 39 519,65 |
| 39 519,65 | 5 315,12 | 1 580,79 | 3 734,33 | 35 785,32 |
| 35 785,32 | 5 315,12 | 1 431,41 | 3 883,70 | 31 901,62 |
| 31 901,62 | 5 315,12 | 1 276,06 | 4 039,05 | 27 862,57 |
| 27 862,57 | 5 315,12 | 1 114,50 | 4 200,61 | 23 661,95 |
| 23 661,95 | 5 315,12 | 946,48 | 4 368,64 | 19 293,32 |
| 19 293,32 | 5 315,12 | 771,73 | 4 543,38 | 14 749,93 |
| 14 749,93 | 5 315,12 | 590,00 | 4 725,12 | 10 024,81 |
| 10 024,81 | 5 315,12 | 400,99 | 4 914,12 | 5 110,69 |
| 5 110,69 | 5 315,12 | 204,43 | 5 110,69 | 0,00 |
Задача № 7.
Рассчитать средневзвешенную цену капитала (WACC) по приведенным данным. Определить изменение показателя при изменении доли акционерного капитала.
| Вариант | ||||||||||
| Акционерный капитал (%) | ||||||||||
| Цена акционерного капитала (%) | ||||||||||
| Долгосрочные долговые обязательства | ||||||||||
| Цена долгосрочных обязательств | ||||||||||
| Изменение доли акционерного капитала (%) | +10 | +5 | +15 | +5 | -10 | -15 | +30 | +25 | +20 | +25 |
Решение:
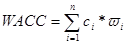 , где
, где
WACC - Средневзвешенная цена капитала, %;
ωi – доля i-го источника в общем объёме;
ci - цена i-го источника.
WACC = 20* 0,8+24*0,2=20,8 %
При изменении доли акционерного капитала на +5%, средневзвешенная цена будет равна:
WACC = 20* 0,85+24*0,15=20,6 %
То есть, уменьшится на 0,2%
Задача № 8.
Определить целесообразность приобретения технологической линии, если известны следующие параметры.
| Вариант | ||||||||||
| Инвестиции в нулевом периоде | ||||||||||
| Генерируемый ежегодный годовой приток (в конце периода) | ||||||||||
| Срок эксплуатации (лет) | ||||||||||
| Ликвидационная стоимость | ||||||||||
| Требуемая норма прибыли |
Решение:
Нам необходимо найти прибыль от приобретения линии. Она представляет собой разницу между генерируемым доходом и расходами на амортизацию.
При этом амортизацию находим как разница между первоначальной и ликвидационной стоимостью линии, поделенной на количество лет эксплуатации.
Амортизация:
(12000-800)/7 = 1600
Прибыль от приобретения линии:
2000 – 1600 = 400
Найдем реальную норму прибыли
400/2000 * 100% = 20%
В нашем случаи реальная норма прибыли больше планируемой, следовательно, приобретение технологической линии целесообразно.
Задача № 9.
На основании приведенных данных методом САРМ определить коэффициент эластичности портфеля однородных ценных бумаг (р) и доходность данного портфеля.
| Вариант | |
| βА | 0,05 |
| βB | 0,85 |
| βC | 1,4 |
| βD | 0,9 |
| βE | 1,7 |
| Безрисковая ставка бр <%) | |
| Средняя доходность рынка (%) |
Состав портфеля инвестора
| Актив | Общая рыночная стоимость (тыс.руб.) |
| А | |
| В | |
| С | |
| D | |
| E |
Коэффициент эластичности портфеля однородных ценных бумаг (р)
Модель САРМ учитывает риск вложения в конкретную бумагу и положение этой ценной бумаги на фондовом рынке.
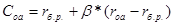 ,где
,где
rб.р. - безрисковая ставка;
rоа - доходность по аналогичным ценным бумагам;
β – коэффициент эластичности по конкретному рынку ценных бумаг;
rоа - rб.р – премия за риск.
Коэффициент β показывает колебание доходности данной ценной бумаги относительно доходности аналогичной ценной бумаге.
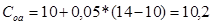 ,
,
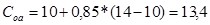 ,
,
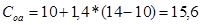 ,
,
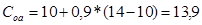 ,
,
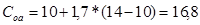 ,
,
Определим доход по каждому активу:
А = 50000 * 10,2% = 5100 тыс. руб.
В = 10000 * 13,4% = 1340 тыс. руб.
С = 25000 * 15,6% = 3900 тыс. руб.
D = 8000 * 13,9% = 1112 тыс. руб.
Е = 7000 * 16,8% = 1176 тыс. руб.
Доходность данного портфеля составит:
5100 +1340 + 3900 + 1112 + 1176 = 12628 тыс. руб.
Доходность портфеля составит:
12628/100000*100 = 12,63%
Коэффициент эластичности составит 0,657
Задача № 10.
Выбрать наиболее эффективный проект из двух предложенных.
| Вариант | ||||||||||
| NPV 1-го проекта (млн.руб.) | ||||||||||
| Срок реализации 1-го проекта (лет) | ||||||||||
| NPV 2-го проекта (млн.руб.) | ||||||||||
| Срок реализации 2-го проекта (лет) | ||||||||||
| Ставка дисконтирования (%) |
Решение:
У нас проекты с разными сроками реализации, то есть они несопоставимы друг с другом. Приведем их к сопоставимому виду.
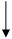 | 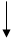 |  |
NPV1=17 NPV1=17 NPV1=17

 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14
i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 











0 1 2 3 4 5 6 7 8 9 10 11 12
 NPV2=10 NPV2=10 NPV2=10 NPV2=10
NPV2=10 NPV2=10 NPV2=10 NPV2=10













 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14
i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14 i=14
0 1 2 3 4 5 6 7 8 9 10 11 12
NPV1= 17+ 17 * 
NPV2= 10+ 10 * 
Так как NPV1 > NPV2 выбираем 1 проект.
Задача №11.
Осуществить пространственную оптимизацию проектов, поддающихся дроблению по приведенным данным.
| Вариант | Денежные потоки по периодам (млн. руб.) | Возможности инвестирования | Ставка дисконтирования (%) | ||||||
| Проект | (млн. руб.) | ||||||||
| А | -30 | ||||||||
| В | -25 | ||||||||
| С | -20 | ||||||||
| D | -10 | ||||||||
Решение:
Для каждого из потоков находим NPV, PI, IRR
| период | Денежный поток А | Коэффициент дисконтирования, при i=16% | NPV1 |
| -30 | -30 | ||
| 0,9091 | 13,6 | ||
| 0,8264 | 16,5 | ||
| 0,7513 | 6,8 | ||
| 0,683 | 3,4 | ||
| период | Денежный поток В | Коэффициент дисконтирования, при i=16% | NPV2 |
| -25 | -25 | ||
| 0,9091 | 4,5 | ||
| 0,8264 | 16,5 | ||
| 0,7513 | 15,0 | ||
| 0,683 | 2,7 | ||
| период | Денежный поток С | Коэффициент дисконтирования, при i=16% | NPV3 |
| -20 | -20 | ||
| 0,9091 | 9,1 | ||
| 0,8264 | 8,3 | ||
| 0,7513 | 7,5 | ||
| 0,683 | 6,8 | ||
| период | Денежный поток D | Коэффициент дисконтирования, при i=16% | NPV4 |
| -10 | -10 | ||
| 0,9091 | 7,3 | ||
| 0,8264 | 9,1 | ||
| 0,7513 | 1,5 | ||
| 0,683 | 4,8 |
| проект | Денежные потоки | NPV | PI | IRR | ||||
| А | -30 | 10,3 | 1,344 | 28,2 | ||||
| В | -25 | 13,7 | 1,553 | 32,6 | ||||
| С | -20 | 11,7 | 1,585 | 34,9 | ||||
| D | -10 | 12,7 | 2,265 | 67,6 |
Срок окупаемости:
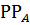 = 1 +
= 1 + 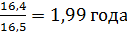
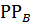 = 2 +
= 2 + 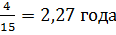
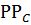 = 2 +
= 2 + 
 = 1 +
= 1 + 
Ранжируем проекты в порядке убывания рентабельности инвестиций:
D C B А
Отбираем проекты в портфель: D+C=10+20=30<40 Þоба проекта реализуются в полном объеме. Находим NPV портфеля: 
Задача № 12.
По условиям предыдущей задачи осуществить пространственную оптимизацию проектов, не поддающихся дроблению.
| Вариант | Денежные потоки по периодам (млн. руб.) | Возможности инвестирования | Ставка дисконтирования (%) | ||||||
| Проект | (млн. руб.) | ||||||||
| А | -30 | ||||||||
| В | -25 | ||||||||
| С | -20 | ||||||||
| D | -10 | ||||||||
| проект | Денежные потоки | NPV | PI | IRR | ||||
| А | -30 | 10,3 | 1,344 | 28,2 | ||||
| В | -25 | 13,7 | 1,553 | 32,6 | ||||
| С | -20 | 11,7 | 1,585 | 34,9 | ||||
| D | -10 | 12,7 | 2,265 | 67,6 |

Следовательно, оптимальный портфель D+B