Каждому числовому промежутку присущи четыре неразрывно связанные между собой вещи:
· название числового промежутка,
· отвечающее ему неравенство или двойное неравенство,
· обозначение,
· и его геометрический образ в виде изображения на координатной прямой.
Любой числовой промежуток может быть задан любым из трех последних по списку способов: либо неравенством, либо обозначением, либо его изображением на координатной прямой. Причем по данному способу задания, например, по неравенству, с легкостью восстанавливаются и другие (в нашем случае обозначение и геометрический образ).
Переходим к конкретике. Опишем все числовые промежутки с указанных выше четырех сторон.
· Начнем с описания числового промежутка, получившего название открытый числовой луч. Заметим, что часто прилагательное «числовой» опускают, оставляя название открытый луч.
Этому числовому промежутку соответствуют простейшие неравенства с одной переменной вида x<a или x>a, где a – некоторое действительное число. То есть, согласно смыслу записанных неравенств, открытый числовой луч составляют все действительные числа, которые меньше числа a (в случае неравенства x<a), или все действительные числа, которые больше числа a (в случае x>a).
Множество чисел, удовлетворяющих неравенству x<a, условились обозначать как (−∞, a), а удовлетворяющих неравенству x>a, как (a, +∞).
Осталось показать геометрическое изображение открытого луча, из него станет видно, что такое название рассматриваемый числовой промежуток получил не случайно. Обратимся к координатной прямой. Известно, что между ее точками и действительными числами имеет место взаимно однозначное соответствие, что позволяет координатную прямую называть числовой прямой. А при разговоре о сравнении чисел мы отметили, что большее число располагается на координатной прямой правее меньшего, а меньшее – левее большего. Исходя из этих соображений, неравенству x<a отвечают все точки координатной прямой, лежащие левее точки с координатой a, а неравенству x>a – точки, лежащие правее точки a. Само число a не удовлетворяет этим неравенствам, чтобы подчеркнуть это на чертеже ее изображают точкой с пустым центром. Над точками, которым соответствуют числа, удовлетворяющие неравенству, изображают наклонную штриховку:
Из приведенных чертежей видно, что данным числовым промежуткам соответствуют части числовой прямой, представляющие собой лучи с началом в точке a, но исключая саму точку a. Другими словами, это лучи без начала. Отсюда и название – открытый числовой луч.
Приведем несколько конкретных примеров открытых числовых лучей. Так строгое неравенство x>−3 задает открытый числовой луч. Его же задает запись (−3, ∞). А на координатной прямой этот числовой промежуток представляет собой множество точек, лежащих правее точки с координатой −3, не включая саму эту точку. Еще пример: неравенство x<2,3, как и запись (−∞, 2,3), задает открытый числовой луч, который следующим образом изображается на координатной прямой
· Переходим к числовым промежуткам следующего вида – числовым лучам. В геометрическом плане их отличие от открытых лучей заключается в том, что начало луча не отбрасывается. Другими словами, геометрический образ числовых промежутков этого вида есть полноценный луч.
Что касается задания числовых лучей с помощью неравенств, то им отвечают нестрогие неравенства x≤a или x≥a. Для них приняты обозначения (−∞, a] и [a, +∞) соответственно, квадратная скобка означают включение записанного рядом с ней числа в множество.
Для наглядности зададим конкретный числовой луч. Неравенству x≥5, как и записи [5, +∞), отвечает множество точек на числовой прямой, представляющее собой луч следующего вида
· Переходим к следующему числовому промежутку – интервалу. Интервалы задаются двойными неравенствами вида a<x<b, где a и b – некоторые действительные числа, причем a меньше b, а x – переменная. То есть, такой числовой промежуток как интервал представляет собой множество всех таких чисел, которые больше, чем a, но меньше, чем b. Для таких интервалов принято обозначение (a, b), круглые скобки указывают на то, что ни число a, ни число b не включаются в множество. На координатной прямой интервал представляет собой отрезок прямой, заключенный между точками с координатами a и b, причем эти точки – концы отрезка – не включаются.
Приведем пример интервала: −1<x<3,5, что то же самое (−1, 3,5), и изобразим его на координатной прямой
· Числовой отрезок – следующий вид числового промежутка – отличается от только что рассмотренного интервала тем, что включает в себя граничные точки. Числовым отрезкам отвечают нестрогие двойные неравенства вида a≤x≤b. В обозначении используются квадратные скобки, в которых через запятую заключены числа a и b: [a, b]. А геометрический образ числового отрезка представляет собой отрезок вместе с его концами:
Например, числовой отрезок, который задается двойным неравенством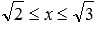 
можно обозначить как 
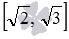, на координатной прямой ему отвечает отрезок с концами в точках, имеющих координаты корень из двух и корень из трех.
· Осталось лишь сказать про числовые промежутки, называемые полуинтервалами. Они представляют собой, если так можно выразиться, промежуточный вариант между интервалом и отрезком, так как включают в себя одну из граничных точек. Полуинтервалы задаются двойными неравенствами a<x≤b или a≤b<c, которым соответствуют обозначения (a, b] и [a, b). Несложно представить и их геометрическую интерпретацию:
Например, полуинтервал (1, 3] можно обозначить как 1<x≤3, а на числовой прямой он представлен отрезком с концами в точках с координатами 1 и 3, причем первую из них следует исключить.
Таблица числовых промежутков
Итак, в предыдущем пункте мы определили и описали следующие числовые промежутки:
· открытый числовой луч;
· числовой луч;
· интервал;
· числовой отрезок;
· полуинтервал.
Для удобства сведем все данные о числовых промежутках в таблицу. Занесем в нее название числового промежутка, соответствующее ему неравенство, обозначение и изображение на координатной прямой. Получаем следующую таблицу числовых промежутков:
