Лабораторная работа № 30
 |
Рис. 30.1. Экспериментальная установка для исследования пропускной
способности короткой безнапорной трубы квадратного сечения
Цель работы – экспериментальное исследование пропускной способности и гидравлического сопротивления безнапорной короткой трубы квадратного поперечного сечения.
Для пропуска невысоких расходов малых рек, а также паводковых и ливневых стоков при пересечении водотоков с автомобильными или железными дорогами под полотнами этих транспортных магистралей устраивают искусственные малые водопропускные сооружения. К таким сооружениям, в частности, относятся малые водопропускные трубы, длина которых не превышает 30 метров. Как правило, такие трубы работают в безнапорном (незатопленном) или полунапорном режиме, когда свободная поверхность воды в трубе находится ниже её потолка, при этом над свободной поверхностью имеется воздушное пространство, т.е. сечение трубы заполнено водой частично. Напорный режим движения воды, при котором труба заполнена водой полностью (см. лабораторную работу № 29), нехарактерен для водопропускных сооружений под транспортными магистралями и может возникать лишь в исключительных случаях при паводках и ливневых стоках, значительно превышающих расчетные.
Условие полунапорного режима соблюдается, когда
 , ,
| (30.1) |
а условием безнапорного режима принимают
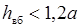 , ,
| (30.2) |
где h вб – глубина воды перед входом в трубу; a – высота или сторона квадратной трубы (рис. 30.1 и 30.2), на лабораторной модели а = 133 мм.

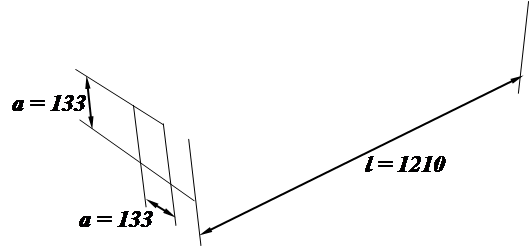 |
Рис. 30.2. Основные конструктивные размеры модели короткой трубы
квадратного поперечного сечения (размеры в миллиметрах)
Движение воды через короткие безнапорные (незатопленные) трубы сопровождается формированием на свободной поверхности потока стоячих волн малой высоты (см. рис. 30.1). Это позволяет сделать вывод о том, что поток в трубе находится в критическом состоянии, при котором его глубина h и скорость V равны критическим
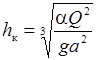
| (30.3) |
и
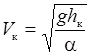 , ,
| (30.4) |
где h к – критическая глубина потока; a – коэффициент Кориолиса, a = 1,03; Q – пропускаемый по трубе расход; g – ускорение свободного падения, g = 9,81 м/с2; a – вданном случае ширина трубы, а = 133 м; V к – критическая скорость потока, равная согласно (30.3) и (30.4)
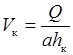 . .
| (30.5) |
Следовательно, движение воды через безнапорные (незатопленные) короткие трубы является частным случаем водослива с широким порогом, при высоте порога равной нулю.
Расход воды через незатопленную короткую трубу независимо от её формы определяется по формуле А. Угинчуса[1]
 , ,
| (30.6) |
в которой m – коэффициент расхода короткой водопропускной незатопленной трубы, для трубы прямоугольного (квадратного) сечения без оголовка принимается равным1 m = 0,32; Н 0 – гидродинамический напор
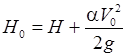 ; ;
| (30.7) |
Н – геометрический (гидростатический) напор
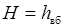 ; ;
| (30.8) |
V 0 – скорость потока в верхнем бьефе на подходе к трубе
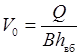 ; ;
| (30.9) |
В – ширина русла или канала в верхнем бьефе перед входом в трубу, равная на модели ширине лабораторного лотка В = 311 мм.
Другим методом определения пропускной способности незатопленной короткой трубы является прямое использование теории Б.А. Бахметьева, применяемой при расчете пропускной способности водослива с широким порогом [3, 6, 7], частным случаем которого и является такая труба. По Бахметьеву сама формула пропускаемого расхода останется прежней (30.6), однако коэффициент расхода трубы не будет константой, а будет иметь вид функции
 , ,
| (30.10) |
здесь j – коэффициент скорости, учитывающий местные потери напора при входе потока в водопропускную незатопленную трубу,
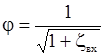 , ,
| (30.11) |
где коэффициент гидравлического сопротивления при внезапном сужении потока при входе в трубу из более широкого лотка согласно И.Е. Идельчику[2] в рассматриваемом случае будет равен
 . .
| (30.12) |
В заключении, используя уравнение Бернулли, следует определить гидравлические потери в короткой незатопленной водопропускной трубе
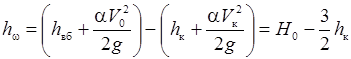 , ,
| (30.13) |
и на начальном участке канала нижнего бьефа при внезапном расширении потока после выхода из трубы
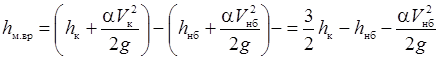 , ,
| (30.14) |
где h нб – глубина потока в отводящем канале нижнего бьефа (см. рис. 30.1); V нб – скорость потока в отводящем канале нижнего бьефа
 . .
| (30.15) |
В процессе выполнения лабораторной работы следует сопоставить экспериментальное значение коэффициента расхода короткой незатопленной трубы, полученное непосредственными измерениями, с его рекомендуемым значением по А. Угинчусу, равным m = 0,32, и вычисленным по Б.А. Бахметьеву и И.Е. Идельчику по формулам (30.10) – (30.12). Необходимо также сопоставить с экспериментальной напор – расходной характеристикой Q – H 0 короткой незатопленной трубы её расчетные характеристики по Угинчусу и по Бахметьеву – Идельчику. И дать оценку точности предлагаемых расчетных методов. Таким образом, основной задачей лабораторной работы является расчетно-опытная проверка соответствия изложенных методов гидравлического расчета пропускной способности короткой незатопленной водопропускной трубы (кульверта) квадратного сечения экспериментальным данным.
Необходимо отметить, что изложенные методы гидравлического расчета справедливы только при турбулентном движении жидкости в области квадратичного сопротивления труб (автомодельной области) при высоких числах Рейнольдса
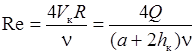 , ,
| (30.16) |
где n – коэффициент молекулярной кинематической вязкости воды, функция связи коэффициента кинематической вязкости с температурой воды приведена в справочнике [6, стр. 13, табл. б/н]; R – гидравлический радиус потока в незатопленной трубе
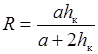 . .
| (30.17) |
На натурных объектах при высоких скоростях и линейных размерах потоков изложенные методы расчета следует полагать должны быть справедливы, на лабораторных моделях при малых скоростях и линейных размерах потоков справедливость изложенных положений подтверждается не всегда. Это следует из теории гидродинамического подобия [2], основы которой применительно к открытым потокам кратко приведены в начале лабораторной работы № 1. Указанные обстоятельства важно учитывать при анализе полученных экспериментальных данных, выделяя область квадратичного сопротивления, в которой коэффициент расхода коротких незатопленных труб не зависит от числа Рейнольдса. В этом случае говорят течение автомодельно по Рейнольдсу.
Методика выполнения лабораторной работы.
1. Перед выполнением лабораторной работы установите гидравлический лоток и регулируемый переливной порог в его отводящем участке в горизонтальное положение. В средней части рабочего участка лотка установите модель короткой водопропускной трубы квадратного поперечного сечения (см. рис. 30.1 и 30.2). Модель установите таким образом, чтобы иметь возможность выполнять измерения отметки уровня свободной поверхности потока в среднем сечении по длине трубы (у с) с помощью пьезометрического щита, а также измерения глубин потока в верхнем бьефе перед входом в трубу (h вб) и в отводящем канале нижнего бьефа (h нб) с помощью шпиценмасштабов. При установке модели смочите водой её резиновые уплотнения и стенки лотка. Обратите внимание на направление движения потока по лотку. Выгните резиновые уплотнения напорной грани модели навстречу движению потока воды в лотке, а резиновые уплотнения низовой грани – по движению потока. Уплотнения не должны быть скручены и должны прилегать к стеклянным стенкам лотка. Убедитесь, что после монтажа модели в лотке не осталось незакрепленных или посторонних предметов, например, винтов, инструментов, протирочных материалов.
2. На двух инструментальных каретках установите электронные шпиценмасштабы (см. рис. 1.6 в лабораторной работе № 1). Для измерения глубины потока в верхнем бьефе (h вб) расположите первую каретку перед моделью трубы таким образом, чтобы игла шпиценмасштаба находилась на расстоянии L = -0,500 м от напорной грани модели. Вторую каретку с электронным шпиценмасштабом установите в нижнем бьефе на таком расстоянии от выходного сечения трубы, на котором глубина потока в лотке стабилизируется и может приниматься равной глубине в отводящем канале нижнего бьефа h нб. Выставьте нули шпиценмасштабов по отметкам дна лотка в створах измерения перечисленных глубин.
3. На пульте управления режимом работы лабораторного лотка или управляющем компьютере задайте пропускаемый по лотку расход 5 м3/час. Включите насос лотка согласно инструкции в лабораторной работе № 1.
4. Перед выполнением опытов выполните измерение температуры воды в лотке и определите её коэффициент кинематической вязкости n, для определения коэффициента кинематической вязкости воды используйте данные справочника [6, стр. 13, табл. б/н]. Запишите температуру и вязкость воды в строку над табл. 30.1 (приведена ниже).
5. Установите в нижнем бьефе короткой трубы квадратного поперечного сечения глубину потока, не допускающую затопление сечения трубы. Для этого регулируемый переливной порог в отводящем участке лотка оставьте в горизонтальном положении.
6. После стабилизации уровня верхнего бьефа перед моделью короткой трубы и гидравлического режима работы лотка (время стабилизации около трех – пяти минут) выполните измерения и запишите в строку табл. 30.1, соответствующую номеру опыта (№), следующих экспериментальных данных:
- пропускаемого расхода Q (измеряется электромагнитным расходомером класса точности 0,3 с диапазоном измерений 0÷150 м3/час);
- глубины потока в верхнем бьефе h вб (измерение производится электронным шпиценмасштабом, выставленным на ноль на отметке дна лотка);
- уровня свободной поверхности потока в среднем сечении по длине трубы у с (измерение производится с помощью пьезометрического щита);
- глубины потока в отводящем канале нижнего бьефа h нб (измерение производится вторым электронным шпиценмасштабом, выставленным на ноль на отметке дна лотка).
7. Увеличьте расход потока на 5 м3/час.
8. Далее повторите действия от пункта 6 до пункта 7. Повторите опыты несколько раз. Последний эксперимент выполните при предельно высоком расходе около 60 м3/час, при котором короткая труба квадратного сечения остается работать в незатопленном режиме.
9. После выполнения программы опытов выключите насос и приборы.
10. После сброса воды из рабочего участка лотка путем непосредственных замеров по пьезометрическому щиту определите и запишите в нижнюю строку табл. 30.1 отметку дна лотка (у дс) в створе измерения уровня свободной поверхности потока в среднем сечении по длине трубы.
11. Далее выполните камеральную обработку и анализ результатов проведенных экспериментальных исследований.
12. В табл. 30.1 наряду с непосредственно измеренными значениями Q, h вб, у с, у дс и h нб запишите результаты вычислений, полученных при обработке опытных данных:
- соотношений глубин воды перед входом в трубу к высоте квадратной трубы h вб/ а (где а = 133 мм), при незатопленной трубе это соотношение должно быть менее 1,2, а при полунапорном режиме – в пределах от 1,2 до 1,4 (см. формулы (30.1) и (30.2));
- глубин потока в среднем сечении по длине трубы
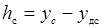 ; ;
| (30.18) |
- критических глубин потока h к (см. формулу (30.3));
- скоростей потока в верхнем бьефе V 0 (см. формулу (30.9)), в канале незатопленной трубы (критических скоростей) V к (см. формулу (30.4)) и в нижнем бьефе V нб (см. формулу (30.15));
- геометрических (гидростатических) напоров Н (см. формулу (30.8));
- гидродинамических напоров Н 0 (см. формулу (30.7));
- коэффициентов расхода m, приведя формулу (30.6) к виду,
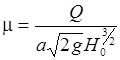 ; ;
| (30.19) |
- гидравлических потерь в короткой незатопленной трубе квадратного сечения h w (см. формулу (30.13));
- гидравлических потерь на начальном участке канала нижнего бьефа при внезапном расширении потока после выхода из трубы h м.вр (см. формулу (30.14));
- чисел Рейнольдса Re (см. формулу (30.16)).
13. В табл. 30.2 (приведена ниже) в соответствии с конструктивными размерами модели короткой трубы квадратного сечения и изменяемыми в процессе опытов расходами Q (см. табл. 30.1) запишите и вычислите расчетные значения:
- коэффициентов расхода короткой водопропускной незатопленной трубы, для трубы прямоугольного (квадратного) сечения без оголовка принимаемых равными по Угинчусу1 m = 0,32;
- гидродинамических напоров по Угинчусу Н 0р.У, приведя формулу (30.6) к виду,
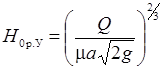 ; ;
| (30.20) |
- невязок между расчетными по Угинчусу Н 0р.У и опытными Н 0 данными
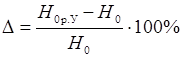 ; ;
| (30.21) |
- коэффициентов Кориолиса, принимаемых равными a = 1,03;
- коэффициентов гидравлического сопротивления при внезапном сужении канала при входе потока из лотка в водопропускную незатопленную трубу zвх (см. формулу (30.12));
- коэффициентов скорости, учитывающих местные потери напора при входе потока в водопропускную незатопленную трубу j (см. формулу (30.11))
- коэффициентов расхода короткой водопропускной незатопленной трубы m по Бахметьеву – Идельчику (см. формулу (30.10));
- гидродинамических напоров по Бахметьеву – Идельчику Н 0р.БИ, приведя формулу (30.6) к виду,
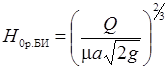 ; ;
| (30.22) |
- невязок между расчетными по Бахметьеву – Идельчику Н 0р.БИ и опытными Н 0 данными
 . .
| (30.23) |
14. По результатам вычислений табл. 30.1 и 30.2 на миллиметровой бумаге формата А4 (210´297 мм) постройте графики экспериментальных и расчетных напор – расходных Q – H 0 характеристик короткой незатопленной трубы квадратного сечения (H 0 = f (Q), H 0р.У = f (Q), H 0р.БИ = f (Q)). На графиках покажите экспериментальные точки замеров, расчетные графики покажите сплошными плавными линиями тренда. Графики, относящиеся к разным расчетным методам, выделяйте цветом карандаша. На той же форматке покажите экспериментальные графики гидравлических потерь в пределах проточного тракта трубы h w = f (Q), потерь за её пределами на выходе в нижний бьеф h м.вр = f (Q) и глубины потока в среднем сечении по длине трубы h с = f (Q). На указанных графиках покажите экспериментальные точки замеров, соединенные плавными линиями тренда. Здесь же покажите расчетную кривую критических глубин в функции пропускаемого расхода h к = f (Q), на расчетной кривой точки расчетов не указываются, сам график покажите сплошной плавной линией тренда.
15. Выполните сопоставительный анализ экспериментальных и расчетных данных по напор – расходным Q – H 0 характеристикам короткой незатопленной трубы квадратного сечения, сопоставьте экспериментальный график функции h с = f (Q) с его расчетным аналогом h к = f (Q). Дайте оценку соответствия экспериментальных и расчетных данных: хорошее соответствие, удовлетворительное, несоответствие.
16. По результатам вычислений табл. 30.1 и 30.2 на другом листе миллиметровой бумаги формата А4 (210´297 мм) постройте графики экспериментальных и расчетных функций изменения коэффициентов расхода короткой незатопленной трубы квадратного сечения от числа Рейнольдса (m = f (Re)). На графиках укажите экспериментальные точки замеров, которые соедините плавными линиями тренда, на расчетных графиках точки расчетов не указываются, сами расчетные графики покажите сплошными плавными линиями тренда. Графики, относящиеся к разным расчетным методам, выделяйте цветом карандаша.
17. Выполните сопоставительный анализ экспериментальных и расчетных данных по коэффициенту расхода короткой незатопленной трубы квадратного сечения m = f (Re). Дайте оценку соответствия экспериментальных и расчетных данных: хорошее соответствие, удовлетворительное, несоответствие.
Таблица 30.1. Экспериментальное исследование пропускной способности и гидравлического сопротивления
незатопленной короткой трубы квадратного сечения с размерами а = 133 на 133 мм и длиной l = 1210 мм
(температура воды t = ______оС, коэффициент кинематической вязкости воды n =________м2/с)
| № | Опытные данные | Обработка опытных данных | ||||||||||||||
| Q | h вб | у с | h нб | h вб/ а | h с | h к | V 0 | V к | V нб | Н | Н 0 | m | h w | h м.вр | Re | |
| м3/час | мм | мм | мм | – | м | м | м/с | м/с | м/с | м | м | – | м | м | – | |
| 0,0 | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
Таблица 30.2. Расчетная пропускная способность незатопленной короткой трубы
квадратного сечения с размерами а = 133 на 133 мм и длиной l = 1210 мм
| № | Q | по Угинчусу | по Бахметьеву – Идельчику | |||||||
| m | Н 0р.У | D | a | zвх | j | m | Н 0р.БИ | D | ||
| м3/час | – | м | % | – | – | – | – | м | % | |
Работа принята......................................................
[1] Ухин Б.В., Мельников Ю.Ф. Инженерная гидравлика: учебное пособие / Под редакцией Б.В. Ухина. Москва: Издательство АСВ, 2007. – 344 с.
[2] Идельчик И.Е. Справочник по гидравлическим сопротивлениям / Москва: Книга по Требованию, 2012. – 466 с.