Операции над событиями
Суммой или объединением двух событий А и В называется событие С, состоящее в наступлении хотя бы одного из событий А или В (безразлично, какого именно, или обоих вместе, если это возможно).
Символически записывают так:
С = А + В или С = А 
В.
Сумма событий интерпретируется как объединение (сумма) множеств.
Если события изображать в виде областей на плоскости, то операция сложения допускает геометрическую интерпретацию:
| 
|
а) соответствует случаю, когда события А и В несовместны.
б) соответствует случаю, когда А и В совместные события.
Из определения суммы событий вытекают следующие свойства.
Свойства сложения
1) А + В = В + А (коммутативность)
2) (А + В) + С = А + (В + С) (ассоциативность)
3) А +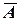 
= U (достоверное событие)
Произведением или пересечением двух событий А и В называется событие С, состоящее в одновременном наступлении А и В.
Символически произведение записывают так:
или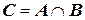 
.
Геометрически произведение 
изображено на (рис. б) в виде заштрихованной области.
Для произведения событий имеют место свойства:
1) 
(коммутативность)
2) 
(ассоциативность)
3) 
(дистрибутивность)
4) 
(невозможное событие)
Ясно, что понятие пересечения и объединения событий переносятся на произвольное число событий.
Суммой или объединением нескольких событий А 1, А 2,... А n называется событие С, состоящее в наступлении хотя бы одного (по крайней мере одного) из событий А 1, А 2,... А n.
или 
Произведением или пресечением нескольких событий А 1, А 2,... А n называется событие С, состоящее в одновременном наступлении всех событий А 1, А 2,... А n.
или 
Пример. Найти сумму событий:
1) Испытание – бросание игральной кости.
А – «появление одного очка»;
В – «появление двух очков»;
С – «появление трех очков».
Ответ: А + В + С = D – «появление не более трех очков».
2) Испытание – приобретение лотерейных билетов.
А – «выигрыш 100 рублей»;
В – «выигрыш 200 рублей»;
С – «выигрыш 300 рублей».
Ответ: А + В + С = D – «по лотерее выиграно либо 100, либо 200, либо 300 рублей.
Пример. Найти произведение событий:
1) Испытание – два выстрела по мишени.
А – «попадание первым выстрелом»;
В – «попадание вторым выстрелом».
Ответ: 
- «попадание первыми двумя выстрелами».
2) Испытание – бросание игральной кости.
А – «непоявление трех очков»;
В – «непоявление пяти очков»;
С – «появление нечетного числа очков».
Ответ: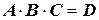 
- «появление одного очка».
Мы уже вычисляли вероятность события непосредственно, исходя из определения. Этот путь приводит к верному ответу только в самых простых случаях. Обычно же прямой подсчет, как всех исходов, так и тех из них, которые являются благоприятствующими, оказывается неудобным, а иногда и практически невозможным из-за своей сложности. Вычисление вероятности можно упростить, если использовать теоремы, устанавливающие связи между вероятностями событий.
Операции над вероятностями
Теорема 1: Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий, т.е.
Доказательство. Пусть событию А благоприятствуют k исходов, событию В – l исходов. События А и В несовместны, поэтому, если n – общее число равновозможных несовместных элементарных событий, в результате которого может произойти одно из событий А или В, то среди них нет таких, которые одновременно благоприятствовали бы и событию А и событию В. Следовательно, событию А+В будет благоприятствовать ровно k+l исходов. По определению вероятности имеем:
т.е. 
что и требовалось доказать.
Эта теорема называется теоремой сложения несовместных событий.
Из этой теоремы вытекают некоторые следствия:
Следствие 1. Сумма вероятностей противоположных событий равна единице, т.е.
Доказательство. Поскольку события 
и 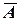несовместны, то к ним применима теорема сложения: 
но событие 
достоверное, поэтому:
Следствие 2. Вероятность суммы нескольких несовместных событий 
равна сумме вероятностей этих событий, т.е.
Теорема 2: Если события А и В совместны, то вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения (совместного наступления обоих событий).
Доказательство. Пусть событию А благоприятствуют к исходов, событию В – l исходов и пусть среди l+k событий содержится q исходов, благоприятствующих совместному осуществлению событий А и В. Тогда, если число всех исходов равно n, то по определению вероятности имеем:
Событию А+В будут благоприятствовать k+l-q исходов (т.к. событие А+В состоит в том, что произошло или событие А, или событие В, или и то и другое).
Поэтому: 
, что и требовалось доказать.
Теорема может быть обобщена на любое конечное число совместных событий.
Для трех совместных событий имеет место формула:
Теорема 3: Вероятность произведения двух независимых событий равна произведению вероятностей этих событий, т.е.
Доказательство. Пусть 
- число равновозможных элементарных событий испытания, в результате которого событие А может произойти или не произойти; 
- число элементарных событий, благоприятствующих событию 
; 
- число равновозможных элементарных событий испытания, в результате которого может событие В; 
- число элементарных событий, благоприятствующих событию 
.
Очевидно, что общее число элементарных событий испытания, в результате которого может произойти (или не произойти) событие АВ, равно 
. Так как события А и В независимы, то число элементарных событий, благоприятствующих событию АВ, равно 
.
Поэтому: 
.
Если имеем 
попарно независимых событий 
, то
Теорема 4: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие произошло.
,
- условная вероятность события А.
В случае произвольных событий имеет место формула:
,
где 
- вероятность события 
, вычисленная при условии, что произошли события .
Пример1. На стеллаже библиотеки в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие А).
Решение
Способ 1. Требование – хотя бы один - будет осуществлено, если произойдет любое из следующих трех несовместимых событий:
В – один учебник в переплете, два без переплета;
С – два учебника в переплете, один без переплета;
D – три учебника в переплете.
Интересующее нас событие А (хотя бы один из взятых трех учебников в переплете) можно представить в виде суммы этих событий:
.
По теореме сложения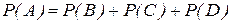 
,
где 
, 
, 
.
Способ 2. Событие А – «хотя бы один из взятых трех учебников имеет переплет» и А – «ни один из взятых учебников не имеет переплета» - противоположные, поэтому 
(сумма вероятностей двух противоположных событий равна единице).
Значит, 
.
; 
.
Пример 2. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобрано 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение
Пусть событие А – первым отобран мужчина;
В – вторым отобран мужчина;
С – третьим отобран мужчина.
,
(события А, В, С – зависимые).
Пример 3. Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута пика или туз.
Решение
События А (выбрана пика) и В (появился туз) – совместные, поэтому:
Р(пика или туз)= 
.
План 2004/2005, поз.
Ермаш Елена Николаевна