Кафедра САПР ВС
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
на курсовую работу
по дисциплине «Автоматизация конструкторского и технологического проектирования»
на тему: «Алгоритм Краскала трассировки проводного монтажа»
Выполнил: Горбунов Р.Ю.
Проверил: доц. кафедры САПР ВСКарманов П.В.
Рязань 2014
Содержание
Введение
. Практическая и математическая постановка задачи
. Анализ существующих алгоритмов решения задачи
. Описание разрабатываемого алгоритма, его укрупненная схема
. Развернутая блок схема алгоритма
. Контрольный пример
. Перечень идентификаторов
. Текст программы
. Листинг с результатами машинного решения
Заключение
Список литературы
Введение
Внедрение в инженерную практику методов автоматизации проектирования позволяет перейти от традиционного моделирования разрабатываемой аппаратуры к ее моделированию с помощью персональных компьютеров (ПК). И более того, с помощью ПК возможно осуществить цикл сквозного проектирования, включающий в себя: синтез структуры и принципиальной схемы устройства; анализ его характеристик в различных режимах, синтез топологии, включая размещение элементов на плате или кристалле и разводку межсоединений; верификацию топологии; выпуск конструкторской документации.
Проектирование схем соединений, иначе трассировка соединений, является одной из наиболее трудных задач в общей проблеме автоматизации проектирования электронных устройств. Прежде всего, это связано с многообразием способов конструктивно-технологической реализации соединений, каждый из которых обуславливает использование специфический критериев оптимизации и ограничений при алгоритмическом решении задачи трассировки.
В данном курсовом проекте будет рассматриваться алгоритм Краскала трассировки проводного монтажа.
алгоритмический трассировка монтаж печатный
Практическая и математическая постановка задачи
Трассировка заключается в определении конкретной геометрии печатного или проводного монтажа, реализующего соединения между элементами схемы. Исходными данными для трассировки являются список цепей, метрические параметры и топологические свойства типовой конструкции и её элементов и результаты решения задачи размещения, по которым находятся координаты выводов элементов. Формальная постановка задачи трассировки и методы её решения в значительной степени зависят от вида монтажа (проводной или печатный) и конструктивно-технологических ограничений, определяющих метрические параметры и топологические свойства монтажного пространства.
В типовых конструкциях, начиная с блока и выше, довольно широко используется проводной монтаж, что объясняется высокой трудоёмкостью проектирования и сложностью изготовления печатного монтажа. Изготовление печатного монтажа усложняется с увеличением размеров коммутационных плат, а надёжность его падает. Проводной монтаж может осуществляться по прямым, соединяющим выводы элементов, или с помощью жгутов, которые прокладывают в специальных каналах. Основные ограничения - количество проводников, которые можно подсоединить к одному выводу (обычно не более трёх), и число проводов в каждом жгуте - пропускная способность канала.
Трассировка проводного монтажа заключается в определении порядка соединения выводов в соответствии с принципиальной электрической схемой с учётом заданных ограничений. Критерием качества, как правило, является минимум суммарной длины соединений. Нахождение порядка соединения в выводах элементов внутри цепи сводится к задаче построения на фиксированных вершинах минимального покрывающего или связывающего дерева. Будем использовать модель схемы в виде графа, в котором выводам элементов сопоставлены вершины и на этих вершинах строится полный подграф. Таким образом, каждая цепь представляется отдельной компонентой связности. Необходимо построить минимальные покрывающие деревья на тех компонентах связности, число вершин в которых больше двух. Напомним, что в результате размещения элементов определены координаты их выводов в соответствующей метрике, т.е вершины компонент связности отображены в граф решётки монтажного пространства.
Расстояние между каждой парой вершин полного подграфа для проводников, идущих по кратчайшему направлению:
 , (1)
, (1)
для ортогональной трассировки
 . (2)
. (2)
Здесь  и
и  - координаты i-й и j-й вершин графа.
- координаты i-й и j-й вершин графа.
Будем использовать модель схемы(цепи) в виде графа, в к-м выводов элементов сопоставлены вершины и на этой вершине строится полный граф цепи. Число вершин графа = n, при этом число ребер полного графа r=n(n-1)\2 При таком подходе каждая цепь представляется отдельной компонентой связности.
Ставится задача построения КСД на тех комп-х связности число вершин которых>2.
Отметим, что на n вершинах полного графа можно построить tn деревьев.

Точные решения задачи построения КСД методом полного перебора нецелесообразны. Существуют приближенные алгоритмы решения этой задачи, дающие результаты достаточно близкие к оптимальным.
Алгоритм Краскала
Пусть задан G=(X,V) i,j=1,n, i≠j
Каждому ребру Vij поставлено в соответствие число Cij - вес или длина данного ребра.
Ставится задача: среди всех деревьев (n-(n-2)), кот. м. выделить в данном графе, требуется найти дерево с минимальной длиной в дереве (n-1) ребро.
Пусть C=[cij]n*n матрица длины ребер графа.
. Все ребра графа n(n-1)\2 упорядочиваются в порядке убывания длины, начиная с ребра C1=mini,jCij, Cn=maxi,jCij
. Последовательно просматривается рассматриваемое множество V* длин ребер на каждом шаге, включенным в дерево одно ребро. В качестве такого ребра выбирается ребро среди не включенных в дерево, имеющих минимальную длину и не образующих циклов с ребрами уже вошедших в дерево.
. Отметим: при работе этого алгоритма возможно появление несвязных поддеревьев, которое затем соединяется, образуя одну компоненту связности.
На рис 1. показан процесс построения минимального покрывающего дерева алгоритмом Краскала.
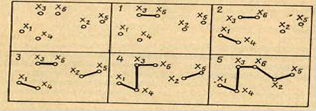
Рис 1.