Из многообразия классических задач механики контактного взаимодействия для анализа моделирования контакта в программном комплексе ANSYS выбрано два варианта контактного взаимодействия сферического штампа с пространством и сферой. Выбор контакта сферического штампа с разными объектами связан с тем, что такое классическое контактное взаимодействие близко к контакту элементов сферических опорных частей: контакт сферического сегмента со стальной плитой через антифрикционную полимерную прослойку.
Рассмотрим аналитическое решение задач: вдавливания сферического штампа в пространство и вдавливания сферического штампа в сферу большего радиуса.
Задача о вдавливании стального сферического штампа в полимерное пространство без трения. Упругий сферический штамп радиуса R вдавливается в упругое полимерное пространство (рис.2.2.), где d – глубина проникновения сферического штампа в пространство, a – радиус области контакта.

|

|

|
| Рис. 2.2. Контакт сферического штампа с пространством. |
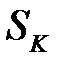
|

|
Глубина проникновения и радиус образовавшейся области контакта имеют следующую зависимость:
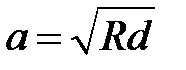 . (1)
. (1)
Величина нагрузки, необходимой для вдавливания сферического штампа в упругое пространство на глубину d равна
 , (2)
, (2)
где  ,
,  и
и  - модули упругости,
- модули упругости, 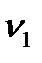 и
и  - коэффициенты Пуассона обоих тел.
- коэффициенты Пуассона обоих тел.
Распределение контактного давления по контактной поверхности определяется по формуле:
 , (3)
, (3)
где  .
.
В качестве материла сферического штампа и упругого пространства выбраны модифицированный фторопласт и сталь соответственно. В таб. 2.1. приведены свойства материалов и характеристики контакта, полученные в результате аналитического решения задачи.
Таблица №2.1.
Основные характеристики материалов, геометрии и нагрузки
| Параметр | Значение |
| E1 | 8.64E+08 Па |
| E2 | 2.00E+11 Па |
| nu1 | 0.461 |
| nu2 | 0.3 |
| E* | 1.09E+09 Па |
| R | 1 м |
| a | 0.1 м |
| d | 0.01 м |
| P | 1.46E+06 Н |
| p0 | 69536439.05 Па |
Аналитическое решение, полученное при заданных механических характеристиках материалов сферического штампа и пространства, а так же их геометрических размеров и величины нагрузки приведено, ниже, в табл.2.
Таблица №2.2.
Аналитическое решение
| a, м | 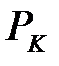 , Па , Па
|
| 0.01 | |
| 0.02 | 68096977.9 |
| 0.03 | 66299906.9 |
| 0.04 | 63698890.1 |
| 0.05 | 60189793.6 |
| 0.06 | 55600949.6 |
| 0.07 | 49633775.3 |
| 0.08 | 41700712.2 |
| 0.09 | 30294865.1 |
| 0.1 | 0.0 |
Распределение контактного давления по радиусу области контакта сферического штампа и пространства  (Табл. 2.2.) представлено на рис. 2.3., так как аналитическое решение не учитывает трение по сопрягаемым поверхностям значение контактного касательного напряжения равно нулю на всей области контакта.
(Табл. 2.2.) представлено на рис. 2.3., так как аналитическое решение не учитывает трение по сопрягаемым поверхностям значение контактного касательного напряжения равно нулю на всей области контакта.

 , Па , Па
|
 , м , м
|
| Рис. 2.3. Контактное давление по радиусу области контакта. |
Полученное распределение контактного давления для задачи о вдавливании сферического упругого штампа в упругое полимерное пространство качественно не противоречит результатам решения аналогичных задач [10, 12 и др.].
Задача о вдавливании стального сферического штампа в сферу большего радиуса без трения. Изначально две упругие сферы имеют одну точку контакта (рис.2.4.), в результате действия нагрузки область контакта увеличивается и при этом область контакта представляет собой площадку в форме круга некоторого радиуса  , при этом d – глубина проникновения сферического штампа в сферу.
, при этом d – глубина проникновения сферического штампа в сферу.
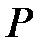
|
| a |
| d |
| Рис. 2.4. Контакт сферического штампа со сферой большего радиуса. |
Радиус площадки контакта  находится по формуле:
находится по формуле:
 ,
,
где  и
и 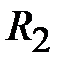 - радиусы сферического штампа и нижней сферы соответственно.
- радиусы сферического штампа и нижней сферы соответственно.
При контакте сферического штампа со сферой, уравнения (1)-(3), которые определяют необходимую величину нагрузки, распределение контактного давления по поверхности контакта, справедливы и для этой тестовой задачи соответственно для радиуса:
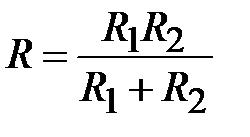 .
.
В качестве материла сферического штампа радиусами  и сферы радиуса
и сферы радиуса 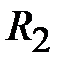 выбраны модифицированный фторопласт и сталь соответственно. В таб. 2.3. приведены свойства материалов и характеристики области контакта, полученные в результате аналитического решения задачи.
выбраны модифицированный фторопласт и сталь соответственно. В таб. 2.3. приведены свойства материалов и характеристики области контакта, полученные в результате аналитического решения задачи.
Таблица №2.3.
Основные характеристики материалов, геометрии и нагрузки
| Параметр | Значение |
| E1 | 8.64E+08 Па |
| E2 | 2.00E+11 Па |
| nu1 | 0.461 |
| nu2 | 0.3 |
| E* | 1.09E+09 Па |
| R1 | 1 м |
| R2 | 1.5 м |
| R | 0.6 м |
| a | 0.02 м |
| d | 0.02 м |
| P | 1127525.729 Н |
| p0 | 89725646.64 Па |
Аналитическое решение, полученное при заданных механических характеристиках материалов сферического штампа и сферы, а так же их геометрических размеров и силы вдавливания приведено, ниже, в табл.2.4.
Таблица №2.4.
Аналитическое решение
 , м , м
| 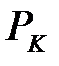 , Па , Па
|
| 89725646.6 | |
| 0.01 | 89021905.2 |
| 0.02 | 86876483.8 |
| 0.03 | 83177900.6 |
| 0.04 | 77704689.4 |
| 0.05 | 70042060.5 |
| 0.06 | 59347936.8 |
| 0.07 | 43438241.9 |
| 0.08 |
Распределение контактного давления по радиусу области контакта сферического штампа и сферы  (Табл. 2.4.) представлено на рис. 2.5., так как аналитическое решение не учитывает трение по сопрягаемым поверхностям значение контактного касательного напряжения равно нулю на всей области контакта.
(Табл. 2.4.) представлено на рис. 2.5., так как аналитическое решение не учитывает трение по сопрягаемым поверхностям значение контактного касательного напряжения равно нулю на всей области контакта.

 , Па , Па
|
 , м , м
|
| Рис. 2.5. Контактное давление по радиусу области контакта. |
Аналогично первой рассмотренной классической задачи контакта, распределение контактного давления качественно не противоречит результатам решения подобных задач контакта [10, 12 и др.].