Отчеты
По вычислительной математике
Работу выполнили студенты 1 курса гр.4151-71
Кабирова П.М. Кириллова Т.В.
Проверила доцент кафедры химической кибернетики Кошкина Л.Ю.
Казань 2016г.
Оглавление
Тема 1. Численные методы решения алгебраических уравнений. 3
Решение. 3
Отделение корней. 3
Уточнение корней. 4
1.Метод половинного деления. 4
2.Метод касательных. Элементы Ньютона. 4
3. Метод хорд. …………………………………………………….5
4.Метод простых интераций……………………………………………………………….6
5.Листинг программ………………………………………………………………………..7
6.Таблица с результатами………………………………………………………………….8
7.Вывод……………………………………………………………………………………...9
Тема 1. Численные методы решения алгебраических уравнений
В общем виде представлено уравнение с одним неизвестным, которое можно представить в виде:
f(x)=0
где f(x) определена и непрерывна на интервале [a; b]. Необходимо найти корни уравнения.
Число обращенное f(x) в 0 называется корнем уравнения.
Когда алгебраическое уравнение сложное, то прибегаем к использованию приближенного нахождения корней уравнения.
При использовании численных методов решение ищется в 2 этапа:
I этап – отделение корней, т.е. нахождение малого интервала [a;b] внутри которого находится корень уравнения.
Решение
Отделение корней
1) Откроем свой пользовательский файл в табличном процессоре Excel.
2) Для отделения корней получим таблицу значений аргумента и функций на интервале [-5;5]. Для этого в ячейку A1 на Листе1 введем x=, в B1 введем y=.
3) Для построения графика выделим A1:B12, выполним Вставка-Диаграмма, выберем точечную диаграмму, дадим название осям и диаграмме.
II этап – уточнение корней, т.е. нахождение корня с заданной точностью.
Уточнение корней
Далее переходим в редактор Visual Basic (Сервис – Макросы – Редактор Visual Basic) и набираем программы по приведенным в лекциях алгоритмам.
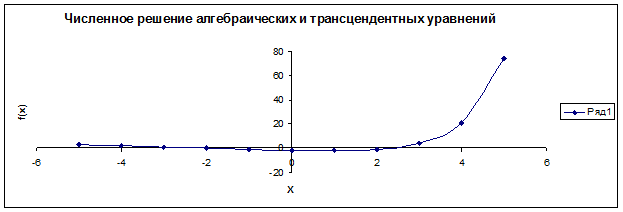
1.Метод половинного деления
В методе половинного деления интервал [a,b] делится пополам.
Алгоритм решения:
Function f(x)
f = x ^ 4 - x - 1
End Function
Sub MPD()
a = 1
b = 2
E = 0.001
n = 0
y1 = f(a)
Do
x = (a + b) / 2
y2 = f(x)
If y1 * y2 > 0 Then
a = x
Else
b = x
End If
n = n + 1
Loop While Abs(b - a) >= E
Worksheets("Лист1").Range("E2").Value = x
Worksheets("Лист1").Range("F2").Value = f(x)
Worksheets("Лист1").Range("G2").Value = n
End Sub.
Метод касательных. Элементы Ньютона.
Основан на замене функции в точке начального приближения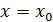 
касательная пересеченная с осью Ox дает первое приближение.
Находим первое приближение по формуле:
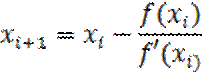
В качестве первого приближения выбирают тот из концов интервала для которых выполняется:
Процесс вычисления продолжается до тех пор пока не выполнится окончательное условие:
Алгоритм решения:
Sub Мкасат()
x = 0
E = 0.001
n = 0
h = 10 ^ -6
Do
pr = (fnx(x + h) - fnx(x)) * h
x1 = x - f(x) / pr
c = Abs(x1 - x)
x = x1
n = n + 1
Loop While Abs(b - a) >= E
Worksheets("Лист1").Range("E3").Value = x
Worksheets("Лист1").Range("F3").Value = f(x)
Worksheets("Лист1").Range("G3").Value = n
End Sub
Метод хорд
В методе хорд нелинейная функция заменяется линейной в качестве которой берется хорда, прямая стягивает концы интервалов [a,b].
Расчетная формула:
В качестве начального приближения выбирают тот из концов интервала для которого выполняется условие:
Условие окончательного процесса:
Алгоритм решения:
Sub Мхорд()
x = 0
E = 0.001
n = 0
y1 = f(c)
Do
y2 = f(x)
xk = x - y2 * (x - c) / (y2 - y1)
p = Abs(x - xk)
x = xk
n = n + 1
Loop While Abs(b - a) >= E
Worksheets("Лист1").Range("E4").Value = x
Worksheets("Лист1").Range("F4").Value = f(x)
Worksheets("Лист1").Range("G4").Value = n
End Sub
Метод простых итераций
Алгоритм решения:
Sub MPI()
x = 3
e = 0.0001
n = 0
Do
y = Log(x + 2) / Log(3) + 1
c = Abs(x - y)
x = y
n = n + 1
Loop While c > e
Worksheets("Лист1").Range("E5").Value = x
Worksheets("Лист 1").Range("F5").Value = f(x)
Worksheets("Лист1 ").Range("G5").Value = n
End SuB.
| Метод | x | f(x) | n |
| Половинного деления | 2,000061035 | -0,999859866 | |
| Касательных | 2,335085521 | 9,41021E-08 | |
| Хорд | 2,335097066 | 4,35345E-05 | |
| Простой итерации | 2,33509642 | 4,11037E-05 |
Вывод:
Если сравнивать сложность алгоритм рассмотренных выше методов, то все они достаточны просты. Метод половинного деления всегда сходится и имеет корень на рассматриваемом интервале, это удобно, т.к. не надо исследовать функцию выбирать первое приближенное для x. Но этот метод, как правило, требует большего числа итерации, чем другие рассматриваемые методы.
Время решения уравнений зависит от количества итераций и времени, затрачиваемого на одну итерацию. Время одной итерации зависит от того, сколько раз вычисляется функция и (если это требуется) её производная на одной итерации. Во всех рассмотренных алгоритмах функция на каждой итерации вычисляется один раз. Но в методе касательных (Ньютона) необходимо вычислить ещё и производную функции. Если сравнивать количество итераций, то все зависит от вида функции. В большинстве случаев меньше всего итераций требует метод касательных (в данном примере еще и метод хорд, где n=5).
Наименьшая погрешность для рассматриваемого примера в методе касательных. Следовательно, самым точным и быстрым методом для рассматриваемой функции f(x)= 3^(x-1)-2-x является метод касательных.
Тема 2. Численные решения систем алгебраических уравнений (СЛАУ).
В общем виде СЛАУ можно представить в виде:
x- неизвестные
а- матрица
b- вектор свободных членов
Различают 2 группы методов:
1. Прямые(точные) методы, к которым относятся:
А) Метод обратной матрицы
Б) Метод Крамера
В) Метод Гауcса
Эти методы можно применить, когда число уравнений в системе не велико, они позволяют получить абсолютно точный результат.
2. Итерационные методы. Это методы последовательных приближений.
а) Метод простой итерации
б) Метод Гаусса-Зейделя
Задание:
Дана система:
7,6х1+5х2+2,4 х3= 1,9
-1,3 х1+0,2 х2+5,8 х3=-1,4
2,2х1+9,1х2+4,4х3=9,7
Решение:
Метод обратной матрицы
Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений.
Суть метода
3. Пусть задана система линейных уравнений с неизвестными:
Эту систему можно записать в виде матричного уравнения А*Х=В,
где А– матрица системы,
Х-столбец неизвестных,
В – столбец свободных коэффициентов.
Из полученного матричного уравнения необходимо выразить Х. Для этого умножим обе части матричного уравнения слева на А^-1, получим:
Х=А^-1*В
Далее находится обратная матрица и умножается на столбец свободных членов.
Метод Крамера
Этот метод применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Δ - главный определитель
Δi-определитель, полученный путем замены
i-го столбца вектором свободных членов
Метод Гаусса
Этот метод основан на:
1. Прямой ход. Приведение матрицы коэффициентов А к треугольному виду, путем математических преобразований.
2. Обратный ход. Нахождение неизвестных, начиная с последнего уравнения.
Метод простой итерации
Листинг программ:
SubGauss()
n = 3
Dim a(1 To 3, 1 To 3) As Variant
Dim b(1 To 3) As Variant
Dim x(1 To 3) As Variant
For i = 1 To 3
For j = 1 To 3
a(i, j) = Worksheets("Лист2").Cells(i, j).Value
Next j
Next i
For i = 1 To 3
b(i) = Worksheets("Лист2").Cells(i, 5).Value
Next i
For k = 1 To n - 1
For i = k + 1 To n
m = a(i, k) / a(k, k)
For j = k + 1 To n
a(i, j) = a(i, j) - m * a(k, j)
Next j
b(i) = b(i) - m * b(k)
Next i
Next k
x(n) = b(n) / a(n, n)
For i = n - 1 To 1 Step -1
S = 0
For j = i + 1 To n
S = S + a(i, j) * x(j)
Next j
x(i) = (b(i) - S) / a(i, i)
Next i
For i = 1 To n
Worksheets("Лист2").Range("B28").Value = x(i)
Next i
Sub MPI()
n = 3
Dim a(1 To 3, 1 To 3) As Variant
Dim b(1 To 3) As Variant
For i = 1 To 3
For j = 1 To 3
a(i, j) = Worksheets("Лист3").Cells(i, j).Value
Next j
Next i
For i = 1 To 3
b(i) = Worksheets("Лист3").Cells(i, 5).Value
Next i
x10 = 0: x20 = 0: x30 = 0
e = 0.001
Do
x1 = (b(1) - (a(1, 2)) * x20 - (a(1, 3)) * x30) / a(1, 1)
x2 = (b(2) - (a(2, 1)) * x10 - (a(3, 1)) * x30) / a(2, 2)
x3 = (b(3) - (a(3, 1)) * x10 - (a(3, 2)) * x20) / a(3, 3)
c = Abs(x1 - x10) + Abs(x2 - x20) + Abs(x3 - x30)
x10 = x1
x20 = x2
x30 = x3
k = k + 1
Loop While c >= e
Worksheets("Лист3").Cells(i, 15).Value = x1
Worksheets("Лист3").Cells(i, 15).Value = x2
Worksheets("Лист3").Cells(i, 15).Value = x3
End Sub
Sub GaussZedel()
n = 3
Dim a(1 To 3, 1 To 3) As Variant
Dim b(1 To 3) As Variant
For i = 1 To 3
For j = 1 To 3
a(i, j) = Worksheets("Лист3").Cells(i, j).Value
Next j
Next i
For i = 1 To 3
b(i) = Worksheets("Лист3").Cells(i, 5).Value
Next i
x10 = 0: x20 = 0: x30 = 0
e = 0.001
Do
x1 = (b(1) - a(1, 2) * x20 - a(1, 3) * x30) / a(1, 1)
x2 = (b(2) - a(2, 1) * x1 - a(3, 1) * x30) / a(2, 2)
x3 = (b(3) - a(3, 1) * x1 - a(3, 2) * x2) / a(3, 3)
c = Abs(x1 - x10) + Abs(x2 - x20) + Abs(x3 - x30)
x10 = x1
x20 = x2
x30 = x3
k = k + 1
Loop While c >= e
Worksheets(«Лист3).Range("R1").Value = x1
Worksheets("Лист3").Range("R2").Value = x2
Worksheets("Лист3").Range("R3").Value = x3
End Sub
Таблица с результатами:
| Метод обратной матрицы | Метод Крамера | Метод Гаусса | Метод простой итерации | Метод Гаусса-Зейделя |
| -0,53775 | -0,53775 | -0,53775 | -0,53775 | -0,53775 |
| 1,394174 | 1,394174 | 1,394174 | 1,394174 | 1,394174 |
| -0,40998 | -0,40998 | -0,40998 | -0,40998 | -0,40998 |
| K1 | =8 | |||
| K2 | =10 |
Вывод:
Сравнить методы решения уравнений можно по двум параметрам:
1. Сложность алгоритма.
2. Время решения уравнения на компьютере.
Сравнивая методы решения систем линейных алгебраических уравнений мы можем определить какой метод легче использовать, Метод обратной матрицы, самый легкий, т.к не нужно писать программу для вычисления уравнений.