Биология
 Задача №1. В начальный момент времени было 8 бактерий, через 2 ч после помещения бактерий в питательную среду их число возросло до 100. Через сколько времени с момента помещения в питательную среду следует ожидать колонию в 500 бактерий?
Задача №1. В начальный момент времени было 8 бактерий, через 2 ч после помещения бактерий в питательную среду их число возросло до 100. Через сколько времени с момента помещения в питательную среду следует ожидать колонию в 500 бактерий?
Решение. В обозначениях задачи «0» эти данные записываются следующим образом: 

 Значит, требуемое время соответствует значению выражения
Значит, требуемое время соответствует значению выражения  , т.е. примерно через 3 ч 15 мин.
, т.е. примерно через 3 ч 15 мин.
Задача №2. Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида? Решение. Применим для вычисления времени формулу сложных процентов:  где
где  2 тыс. – численность животных по истечению искомого времени;
2 тыс. – численность животных по истечению искомого времени;  5 тыс. – численность животных в начальный момент времени; p = 8 - % сокращения численности животных. Предварительно разделив обе части уравнения на 1000,получим:
5 тыс. – численность животных в начальный момент времени; p = 8 - % сокращения численности животных. Предварительно разделив обе части уравнения на 1000,получим: 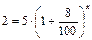

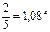 ;
; 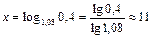 лет. Ответ: приблизительно через 11 лет.
лет. Ответ: приблизительно через 11 лет.
Задача №3. Примером быстрого размножения бактерий является процесс изготовления дрожжей, при котором по мере их роста производится соответствующая добавка перерабатываемой сахаристой массы. Увеличение массы дрожжей выражается показательной функцией:  где
где  первоначальная масса дрожжей, t – время дрожжевания в часах, m – масса дрожжей в процессе дрожжевания. Вычислим m, если
первоначальная масса дрожжей, t – время дрожжевания в часах, m – масса дрожжей в процессе дрожжевания. Вычислим m, если 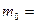 10 кг и t = 9 ч.
10 кг и t = 9 ч.
Решение. Вычислим массу дрожжей в процессе дрожжевания: 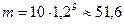 кг.
кг.
Ответ: масса полученных дрожжей:  кг.
кг.
Разбирая задачу №1, нам очень важно понимать его условность. Ведь действительно, мы учитываем только рост численности бактерий, совершенно не интересуясь такими факторами, как естественная смерть бактерий, временная ограниченность питательного компонента (когда его со временем становится меньше), или, скажем, такой экзотический фактор, как наличие в размножающейся колонии бактерий-паразитов и т.п. Учёт всех этих факторов существенно усложнит построение математической модели ситуации и потребует привлечения иных средств математики для её описания. С некоторыми из этих средств мы познакомимся в курсе математического анализа, а впоследствии вы продолжите их изучение в высшем учебном заведении и, если захотите, на профессиональном уровне. Сейчас же заострять на этом внимание не будем.
Задача №4. Известно, что соотношение между углеродом  и его радиоактивным изотопом
и его радиоактивным изотопом  во всех живых организмах постоянно. Период полураспада углерода
во всех живых организмах постоянно. Период полураспада углерода  составляет 5760 лет. Определите возраст останков мамонта, найденных в вечной мерзлоте на Таймыре, если относительное содержание изотопа
составляет 5760 лет. Определите возраст останков мамонта, найденных в вечной мерзлоте на Таймыре, если относительное содержание изотопа  в них составляет 26% от его количества в живом организме.
в них составляет 26% от его количества в живом организме.
Возвращаясь снова к результатам примера 1 и считая, что изначально изотопа  было m, получим:
было m, получим: 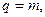

 ,
,  и значит,
и значит,

Итак, возраст останков мамонта составляет примерно 11 200 лет.В природе существуют радиоактивные вещества, которые распадаются с течением времени. Промежуток времени, за который число радиоактивных атомов данного вещества уменьшается вдвое, называется периодом полураспада и обозначается буквой Т.
Химия Наши исследования задач по химии школьного и расширенного курса изучения позволили нам выделить ряд типов задач, при решении которых используются логарифмы:
- равновесные процессы
- гидролиз растворов солей
- скорость химической реакции изучает раздел кинетика
- расчёт рН
Приведём примеры решения данных типов задач.
Равновесные процессы
Задача №1. Константа равновесия реакции СО + Сl2 = COCl2 при 600° равна 6,386. В каком направлении будет протекать реакция, если в 1 л реакционной смеси находятся а) 1 моль CO: 1 моль Сl2 и 4 моль СОСl2 ? Решение. Для решения используем уравнение ∆G = RT 
1)Рассчитываем произведение концентрации веществ:  ; v (СОСl2) = 4 моль;ν (СО) = 1 моль;ν (Сl2) = 1 моль;
; v (СОСl2) = 4 моль;ν (СО) = 1 моль;ν (Сl2) = 1 моль;  = 4
= 4
2) ∆G = RT  ;∆G= RT ln 0,63;∆G < 0, т.к. R>0, T>0, ln 0,63 < 0 (т.к. e>0, 0,63 < 1 по свойству логарифмов), следовательно, самопроизвольно будет протекать прямая реакция.
;∆G= RT ln 0,63;∆G < 0, т.к. R>0, T>0, ln 0,63 < 0 (т.к. e>0, 0,63 < 1 по свойству логарифмов), следовательно, самопроизвольно будет протекать прямая реакция.
Ответ: будет протекать прямая реакция.
Гидролиз растворов солей
Задача №2. Константа скорости гидролиза при 25° равна 3,2 * 10-3 час-1. Рассчитайте а) время за которое гидролизу подвергается 10 % исходного количества сахарозы; б) период полупревращения реакции.
Решение. Рассматриваемая реакция является реакцией первого порядка, т.к. константа имеет размерность час-1.Для ответа на вопрос а) используем уравнение ln  = kτ; cτ = 100% - 10% = 90%
= kτ; cτ = 100% - 10% = 90%
τ =  = 32,9
= 32,9
б) Период полураспада рассчитывают по формуле: τ0,5 =  = 216 час.
= 216 час.