Решение задач линейного программирования
Цельработы: ознакомиться с решением задач линейного программирования в пакетах MATLAB и Maple.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Отдельный класс оптимизационных задач образуют задачи линейного программирования, в которых и оптимизируемый критерий, и ограничения линейны. В них требуется найти экстремум функции  при наличии ограничений в виде неравенств
при наличии ограничений в виде неравенств

Эти условия можно записать в матричной форме
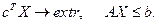 (1)
(1)
Здесь b и c – векторы-столбцы, А – матрица размера m ´ n.
Существует другая форма записи, называемая канонической, когда ограничения имеют вид равенств, а на переменные накладывается требование положительности:
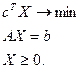 (2)
(2)
Формы записи (1) и (2) не являются независимыми. Существуют преобразования, при помощи которых любую задачу линейного программирования свести к одной из этих форм.
Чтобы перейти к канонической форме (2), необходимо условия типа неравенство заменить на равенства и перейти к положительным переменным. Первое делается путем введения дополнительных переменных, например, вместо неравенства 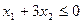 можно записать равенство
можно записать равенство

где  – новая переменная.
– новая переменная.
Любую переменную неопределённого знака можно заменить разностью двух положительных переменных:

Для обратного перехода, от записи (2) к записи (1), ограничения типа равенств нужно заменить неравенствами. Для этого можно воспользоваться формулой:
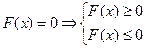 .
.
Например, вместо 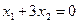 можно записать пару неравенств
можно записать пару неравенств

Существует много методов решения задач линейного программирования. одним из наиболее наглядных является графический метод, а среди численных наиболее известен симплекс-метод. Остановимся на них подробнее.
Графический метод
Применяется, когда число переменных невелико (обычно две), число ограничений может быть любым. На плоскости х,у рисуют прямые, соответствующие ограничениям и рассматривают образованный ими многоугольник. Решение достигается в одной из его вершин. Чтобы найти ее, берут прямую 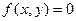 (где
(где 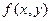 – целевая функция), и перемещают ее параллельно вправо или влево до тех пор, пока многоугольник ограничений не окажется по одну сторону от нее.
– целевая функция), и перемещают ее параллельно вправо или влево до тех пор, пока многоугольник ограничений не окажется по одну сторону от нее.
Симплекс-метод
При решении графическим методом видно, что система ограничений вырезает из пространства параметров некоторый выпуклый многогранник G. При этом в силу выпуклости G и линейности целевой функции экстремум может достигаться только в вершинах G. (В вырожденном случае экстремум может достигаться на всей грани).
Идея симплекс-метода состоит в следующем. На начальном шаге отыскивается любая начальная вершина G и определяются все выходящие из неё ребра. Далее перемещаются вдоль того из ребер, по которому функция убывает (при поиске минимума), и попадают в следующую вершину. Находят выходящие из нее ребра и повторяют процесс. Когда приходят в такую вершину, в которой вдоль всех выходящих из нее ребер функция возрастает, то минимум найден.
Применение симплекс-метода для задачи линейного программирования предполагает предварительное приведение ее к канонической форме (2) с n положительными переменными и m условиями типа равенство.
При этом требование положительности переменных означает, что точки принадлежат области n-мерного пространства, где все координаты положительны (положительный ортант). Равенства определяют n-m мерную гиперплоскость, пересечение которой с положительным ортантом и даёт многогранник допустимых решений.

Рис. 1. Вид допустимого множества для n=2, m=1.
На рис.1 это проиллюстрировано для случая n =3, m =1. При этом условие положительности задаёт положительный октант трёхмерного пространства, а одно (m =1) условие-равенство задаёт двухмерную (n - m =2) плоскость. В результате, допустимое множество, в котором выполняются все условия, становится сечение октанта плоскостью (заштрихованный треугольник). Экстремум линейной целевой функции может наблюдаться только в вершинах этого уймищи, то есть в одной из трёх вершин треугольника.
Чтобы найти вершины многогранника, заметим, что на границе ортанта одна или более переменных равны нулю (на рис.1 на грани (x 1, x 2) переменная x 3=0). Тогда, чтобы найти вершину, нужно как можно большее число переменных приравнять нулю, а остальные найти из условий-равенств. Так как при этом должна возникать система линейных уравнений с n неизвестными, для её однозначного решения необходимо n уравнений, то есть имеющиеся m условий необходимо дополнить n - m равенствами вида xi =0.
Тогда в каждой вершине многогранника будет m ненулевых координат, которые образуют базис. Остальные n - m координат входят в небазисный набор. Обратите внимание, что базис однозначно определяет координаты вершины. Следовательно, задачу можно было бы решить путём полного перебора всех базисов, но их число может быть весьма велико (число выборок по m элементов из n).
Алгоритм симплекс-метода состоит из следующих пяти шагов.
На шаге 0 выбирается начальный базисный набор.
Целевая функция и ограничения-равенства преобразуются к диагональной форме относительно базисных переменных, так, чтобы каждая базисная переменная входила только в одно уравнение и не входила в целевую функцию. Это удобно записать в форме так называемой симплекс-таблицы. В частности, следующая таблица диагонализирована относительно базиса (x 1, x 2, …, x m):
| x1 | x2 | ... | xm | xm+1 | ... | xn | ||
| Базис | Bi\Ci | ... | Cm+1 | ... | Cn | |||
| x1 | B1 | ... | A1,m+1 | ... | A1,n | |||
| x2 | B2 | ... | A2,m+1 | ... | A2,n | |||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| xm | Bm | ... | Am,m+1 | ... | Am,n |
Верхняя строка симплекс-таблицы описывает целевую функцию задачи. Остальные строки соответствует ограничениям задачи. Cвободные члены ограничений составляют крайний левый столбец таблицы. Слева от таблицы записаны текущие базисные переменные (x 1,..., x m), которые входят в уравнение, задаваемое данной строкой. Над таблицей приведен набор всех переменных задачи, где xm+1,..., x n - cвободные переменные задачи.
На шаге 1 проверяется, все ли Ci>=0. Если это так, то такая таблица называется двойственно-допустимой, и соответствует оптимальному решению. Значения базисных переменных в этом случае находятся в столбце B.
Если не все Ci>=0, то на шаге 2 выбирается ведущий столбец (т.е. ведущая переменная), для которого Свед минимально. При увеличении этой переменной критерий уменьшается наиболее быстро.
Увеличивать небазисную переменную можно за счёт базисных, поэтому на шаге 3 выбирается ведущая строка, соответствующая той из базисных переменных, которая будет убывать меньше других. Это та переменная, для которой A i ,вед>0 и отношение Bi/Ai,вед минимально. Если таких переменных нет (все Ai,вед<=0), то задача неразрешима.
После того, как выбраны ведущая строка и столбец, происходит смена базиса, при этом переменная ведущей строки исключается из него (уменьшается до 0), а переменная ведущего столбца, наоборот, вносится (принимает ненулевое значение).
На шаге 4 таблица приводится к диагональному виду уже относительно нового базиса. Для этого линейно комбинируются её строки. В частности, проще всего разделить ведущую строку на значение ведущего элемента (чтобы этот элемент стал равен 1), а затем прибавлять эту строку к другим с таким коэффициентом, чтобы обнулить все остальные элементы ведущего столбца.
Затем осуществляется возврат к шагу 1.
Примеры
Пример 1
Найти максимум и минимум функции 2 x + y при ограничениях 0£ x £1, 0£ y £1.
Геометрическое решение.
Рисуем единичный квадрат и сечем его семейством прямых 2 x + y = с
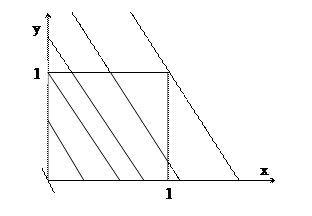
Ясно, что максимум достигается в верхнем правом углу квадрата (точка x =1, y =1) и равен 3, а минимум – в противоположном углу (точка x =0, y =0) и равен нулю.
Решение в MAPLE
В пакете MAPLE для задач линейного программирования нужно загрузить библиотекуsimplex. Для загрузки библиотек служит команда with(<имя библиотеки>). Команды Maple необходимо завершать либо ";", либо, чтобы подавить вывод результата, ":".
Ограничения вводятся в виде списка линейных неравенств. Матричную запись введённой ситемы можно получить при помощи команды display из того же пакета.
После того, как ограничения введены, применяется командаminimize(f, C), если нужно найти минимум целевой функции, либо командаmaximize(f, C), если нужно найти ее максимум, где f – целевая функция, а C – список условий.
> with(simplex):
> e:={x>=0,x<=1,y>=0,y<=1};
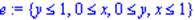
> display(e);

> minimize(2*x+y,e);
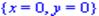
> maximize(2*x+y,e);
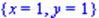
Пример 2
Задача о производстве стульев. Мебельная фабрика может выпускать стулья двух типов, стоимостью 6000 и 12000 рублей. Имеются следующие ресурсы: 440 погонных метров досок, 65 кв.м. обивочной ткани и 320 человеко-часов трудовых ресурсов. На изготовление одного стула требуются следующее количество ресурсов:
| Стул | Расход досок | Расход ткани | Расход времени |
| Первый | 0.5 | ||
| Второй | 0.25 | 2.5 | |
| Ресурс |
Требуется так спланировать производство стульев, чтобы общая цена продукции была максимальной.
Математическая модель
Обозначим х – количество стульев первого типа, у – количество стульев второго типа.
Тогда:
 - оптимизируемый критерий.
- оптимизируемый критерий.
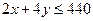 - ограничение по расходу досок
- ограничение по расходу досок
 - ограничение по расходу ткани
- ограничение по расходу ткани
 - ограничение по расходу времени.
- ограничение по расходу времени.
Матричная форма записи:

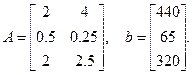
Графическое решение в MATLAB
Для графического решения данной задачи построим на плоскости (x, y) три прямые, соответствующие ограничениям по трем ресурсам. По оси x будем откладывать количество стульев второго вида, по оси y количество стульев первого вида. Полученные графики показаны на рис.2 красным цветом. Они, вместе с осями координат, задают область допустимых решений.
Черным цветом показано семейство прямых 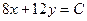 . Решение задачи дает крайняя правая прямая этого семейства, касающаяся многоугольника допустимых решений в точке с координатами (80, 60).
. Решение задачи дает крайняя правая прямая этого семейства, касающаяся многоугольника допустимых решений в точке с координатами (80, 60).
Графики построены в МАТLAB с помощью следующей программы:
x=0:0.2:300; y1=-2*x+220; y2=(-1/2)*x+130; y3=(-5/4)*x+160;
plot(x,y1,x,y2,x,y3); grid; hold on
for c=0:60:1460
y=-3/2*x+c/8;
plot(x,y,'black');grid on;
end
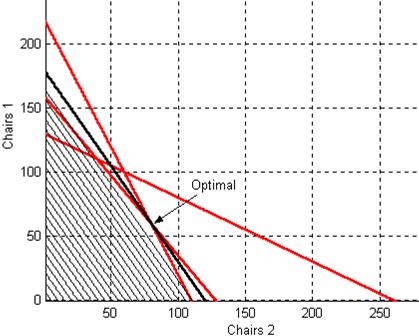
Рис. 2. Графическое решение.