Данный метод извлечения признаков является одним из самых распространённых как в системах распознавания дикторов, так и в системах распознавания речи.
На вход алгоритма подаётся последовательность отсчётов участка сигнала, исследуемого на данной итерации, x0,..., xN-1.
К данной последовательности применяется весовая функция и затем дискретное преобразование Фурье. Весовая функция используется для уменьшения искажений в Фурье анализе, вызванных конечностью выборки. На практике в качестве весовой функции часто используется окно Хэммига, которое имеет следующий вид:

где N — длина окна, выраженная в отсчётах.
Тогда дискретное преобразование Фурье взвешенного сигнала можно записать в виде

Значения индексов k соответствуют частотам

Математические структуры и моделирование. 2011. Вып. 24. 45 где Fs — частота дискретизации сигнала.
Полученное представление сигнала в частотной области разбивают на диапазоны с помощью банка (гребёнки) треугольных фильтров. Границы фильтров рассчитывают в шкале мэл. Данная шкала является результатом исследований по способности человеческого уха к восприятию звуков на различных частотах. Перевод в мэл-частотную область осуществляют по формуле

Обратное преобразование выражается как

Пусть NFB — количество фильтров (обычно используют порядка 24 фильтров), (flow, fhigh) — исследуемый диапазон частот. Тогда данный диапазон переводят в шкалу мэл, разбивают на NFB равномерно распределённых перекрывающихся диапазона и вычисляют соответствующие границы в области линейных частот. Обозначим через Hm,k — весовые коэффициенты полученных фильтров. Фильтры применяются к квадратам модулей коэффициентов преобразования Фурье. Полученные значения логарифмируются
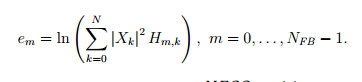
Заключительным этапом в вычислении MFCC коэффициентов является дискретное косинусное преобразование

Коэффициент с0 не используется, так как представляет энергию сигнала. Количество коэффициентов NMFCC на практике выбирают порядка 12.
Кепстральные коэффициенты на основе линейного предсказания
Суть линейного предсказания заключается в том, что линейной комбинацией некоторого количества предшествующих отсчётов можно аппроксимировать текущий отсчёт
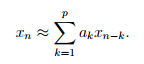
Весовые коэффициенты линейной комбинации a1,..., ap называются коэффициентами линейного предсказания. Нахождение коэффициентов линейного предсказания осуществляют с помощью рекурсивного алгоритма Дарбина.
На основе полученных коэффициентов линейного предсказания рассчитываются кепстральные коэффициенты. Причём таких коэффициентов может быть сгенерировано больше, чем самих коэффициентов линейного предсказания

Для сигнала с частотой дискретизации 8000 Гц используют порядка 12 коэффициентов линейного предсказания, из которых генерируют порядка 18 кепстральных коэффициентов.
Обработка признаков
Описанные выше методы извлечения признаков предназначены для выделения характеристик на небольшом участке. Для того чтобы сохранить информацию о динамике речи, применяют подход, заключающийся в объединении векторов признаков с их первыми и, возможно, вторыми производными. Такие производные получили название ∆- и ∆-∆- коэффициентов (дельта- и дельта-дельта-коэффициентов). На этапе постобработки признаков также применяют методы нормализации, использующие весь набор векторов признаков исследуемой записи. Наибо- лее распространённым методом нормализации, предназначенным для снижения влияния канала, является метод вычитания кепстрального среднего (Cepstral Mean Substraction; CMS). Данный метод предназначен для компенсации изменений между сессиями и в применении к постоянным условиям, наоборот, снижает эффективность.
Методы классификации
Распознавание по голосу отличается от многих биометрических систем тем, что в данном случае предметом распознавания является процесс, а не статическое изображение, как в случае с распознаванием отпечатков пальцев, лица или радужной оболочки глаза. Поэтому чаще всего образец голоса представляется не в виде единого вектора признаков, а в виде последовательности векторов признаков, каждый из которых описывает характеристики небольшого участка речевого сигнала. Последовательность векторов, полученная после этапа обработки сигнала, используется для построения шаблона/модели диктора или для осуществления сравнения с уже построенными шаблонами. Для задач верификации и идентификации может быть определён способ вычисления степеней подобия предъявленного образца с одним или несколькими шаблонами. Степень подобия может вычисляться на основе определённой метрики или на основе оценки вероятности.
Существует несколько способов классификации моделей для задачи рас- познавания. В литературе часто ссылаются на модели как на генеративные или дискриминативные. Суть моделей, которые называют генеративными, заключается в моделировании данных, полученных для обучения, например, с помощью оценки функции плотности вероятности. Примером может служить модель гауссовых смесей. Дискриминативные модели основаны на построении границы между классами, как это реализовано, например, в методе опорных векторов.
Вычисление расстояния
Определение метода вычисления расстояния является основой для шаблон- ных моделей. В таких моделях распознаваемый объект рассматривается как неточная копия одного из хранимых. Одними из самых распространённых методов вычисления расстояния между векторами являются следующие:
• L1-норма (расстояние городских кварталов, манхэттэнское расстояние)
• евклидово расстояние;
• расстояние Махалонобиса.
Метод ближайшего соседа
В качестве шаблона диктора в данном методе используется полный набор векторов обучающей последовательности. Сравнение образца с таким шаблоном происходит следующим образом. Каждый вектор тестовой последовательности сравнивается с каждым вектором шаблона для определения минимального расстояния. Полученные расстояния усредняются для формирования итоговой оценки

Для снижения вычислительной трудоёмкости используют различные методы сокращения шаблона либо методы сохранения данных для ускорения поиска, такие, как, например, kd-дерево или другие методы.
Метод k-ближайших соседей также предписывает сохранение последовательности обучающих векторов, однако вычисление степени подобия происходит несколько иным способом. Для каждого тестового вектора yi после вычисления расстояний до векторов хранимых шаблонов могут быть найдены k ближайших векторов. Пусть kij – количество векторов среди найденных k ближайших, принадлежащие классу j (диктору j в нашем случае). Предполагая более или менее одинаковое количество векторов обучения в каждом классе, оценка вероятности принадлежности вектора i классу j может быть получена как
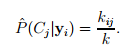
Тогда последовательность векторов может быть классифицирована по правилу
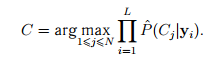
Вместо данного правила (именуемого иногда «правилом произведения») с целью сглаживания эффекта, производимого выбросами, обладающими нулевой или близкой к нулю оценкой вероятности, вводят «правило суммы»

Используя формулу оценки вероятности и учитывая тот факт, что количество соседей k является постоянным, формула может быть переписана как

Такую технику называют схемой голосования, так как последовательность классифицируется к классу, набравшему наибольшее количество «голосов».
Векторное квантование
В методе векторного квантования в отличие от метода ближайшего соседа множество обучающих векторов сохраняется не целиком, а преобразуется в множество (обычно фиксированного размера) кодовых векторов. Распространённым методом построения такого множества, именуемого также кодовой книгой, является алгоритм К-средних.
Алгоритм К-средних разбивает исходное множество на К кластеров, где К — предварительно заданное число. Для этого сначала значения средних инициализируются некоторыми векторами из исходного множества. Затем на каждой итерации алгоритма происходит распределение векторов в ближайшие к ним кластеры (для этого вычисляется расстояние между вектором и текущими значениями средних) и перерасчёт среднего в каждом кластере. Алгоритм Математические структуры и моделирование. 2011. Вып. 24. 49 завершается после того, как на очередной итерации состояния кластеров не изменились либо по достижении заданного максимального количества итераций. Полученные значения средних являются кодовыми векторами, используемыми для построения шаблона. Вычисление расстояния между входной последовательностью векторов и кодовыми книгами осуществляется аналогично методу ближайших соседей.
Модель гауссовых смесей
Модель гауссовых смесей широко используется в области распознавания дикторов. Данная модель представляет собой взвешенную сумму Гауссиан

где λ — модель диктора, M — количество компонентов модели, wi — веса компонентов такие, что

Функция плотности вероятности каждого компонента даётся формулой

где D — размерность пространства признаков, µi — вектор математического ожидания, Σ — матрица ковариации. Чаще всего в системах, реализующих данную модель, используется диагональная матрица ковариации. Возможно также использование одной матрицы ковариации для всех компонентов модели диктора или одной матрицы для всех моделей. Таким образом, для построения модели диктора необходимо определить век- торы средних, матрицы ковариации и веса компонентов. Данную задачу решают с помощью EM-алгоритма. На вход подаётся обучающая последовательность векторов X = {x1,..., xT }. Параметры модели инициализируются начальными значениями и затем на каждой итерации алгоритма происходит переоценка параметров. Для определения начальных параметров обычно используют алгоритм кластеризации такой, как алгоритм К-средних. Построив разбиение множества обучающих векторов на M кластеров, параметры модели могут быть инициализированы следующим образом. Начальные значения µi совпадают с центрами кластеров, матрицы ковариации рассчитываются на основе попавших в данный кластер векторов, веса компонентов определяются долей векторов данного кластера среди общего количества обучающих векторов. Переоценка параметров происходит по следующим формулам:
• вычисление апостериорных вероятностей (Estimation-step)
 ;
;
• вычисление новых параметров модели (Maximization-step)
 .
.
Данные шаги повторяются до схождения параметров.
Метод опорных векторов
Метод опорных векторов является бинарным классификатором и строит разделяющую функцию в виде
f(x) = w · x + b.
Пусть дана обучающая последовательность (x1, y1),...,(xN, yN), где xi — точки пространства признаков, yi — метки, обозначающие принадлежность одному из классов, принимающие значения 1 или −1. Рассмотрим пока случай линейной разделимости данных. Такое ограничение может быть записано в виде

или одним неравенством

Среди возможных разделяющих гиперплоскостей ищется гиперплоскость, создающая максимальный зазор между классами. То есть расстояние от разделяющей гиперплоскости до ближайших точек каждого класса максимально. 1. Данная задача (так же как описываемые далее обобщения на случай линейной неразделимости и введения нелинейности с помощью функции ядра) может быть решена методами квадратичного про- граммирования. Одним из самых популярных является метод, предложенный в. Для того чтобы обобщить задачу на случай линейной неразделимости, ограничения переписывают в виде

Целевая функция принимает вид
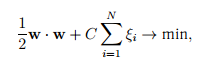
где C — положительная постоянная, задающая степень штрафа за появление ошибок. Другим способом, позволяющим распознавать линейно-неразделимые множества, является введение функции ядра. Идея заключается в том, чтобы отобразить исходное пространство в пространство более высокой размерности, в котором, как может оказаться, множества разделимы. Причём, поскольку всюду в алгоритмах обучения и распознавания признаки используются не отдельно, а в виде скалярных произведений, то нет необходимости в явном виде строить такое преобразование. Достаточно задать функцию ядра, определяющую скалярное произведение в новом пространстве

Среди распространённых можно привести следующие ядра:
 — ядро радиальных базисных функций Гаусса, K(xi, xj) = (xi · xj + 1)n — полиномиальное ядро. Параметры метода (такие как C и параметры ядра) обычно определяют с помощью перебора некоторого множества значений и оценкой методом кроссвалидации.
— ядро радиальных базисных функций Гаусса, K(xi, xj) = (xi · xj + 1)n — полиномиальное ядро. Параметры метода (такие как C и параметры ядра) обычно определяют с помощью перебора некоторого множества значений и оценкой методом кроссвалидации.
Описанные выше методы решают задачу бинарной классификации. Для применения данных методов к задаче многоклассового распознавания используют такие стратегии, как «один-против-остальных» или «один-против-одного». Пусть для обучения получены данные q классов. При использовании стратегии «один-против-остальных» создаются q классификаторов, каждый из которых обучается отличать данный класс от всех остальных. При распознавании объект приписывается к тому классу, чей классификатор выдал наибольшее значение функции f(x). Стратегия «один-против-одного» («каждый против каждого») использует q(q − 1)/2 классификаторов, разделяющих по два класса. Результаты сравнений конкретного класса с каждым из остальных суммируют- ся и затем сравниваются с аналогичными других классов. При этом используют также различные способы преобразования функции f(x) в вероятность P(Ci |x).
Для распознавания последовательности векторов признаков могут быть применены правила, комбинирующие результаты классификации каждого кадра. Используются также подходы, при которых последовательности векторов используются для обучения генеративных моделей, которые затем классифицируются с помощью метода опорных векторов.
Заключение
На первом этапе научно-исследовательской работы были изучены методы извлечения признаков из wave-файла: мэл-частотные кепстральные коэффициенты и кепстральные коэффициенты на основе линейного предсказания, а так же методы обработки признаков wave-файла.
На втором этапе некоторые из этих методов были реализованы в MathCad чтобы сравнить их работоспособность.
На третьем этапе, после тестирования методов, был выбран самые подходящие методы извлечения и обработки для последующего написания на с++.
В целом, после изученных материалов, благодаря опыту других людей в данной сфере, должно получится достаточно надежное программное средство с минимальной вероятностью ошибки.