Задача 1 (вариант 1). Стальной трубопровод диаметром  с коэффициентом теплопроводности
с коэффициентом теплопроводности  покрыт изоляцией в два слоя одинаковой толщиной
покрыт изоляцией в два слоя одинаковой толщиной 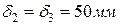 . Первый слой изоляции, накладываемый на поверхность трубы, выполнен из материала с коэффициентом теплопроводности
. Первый слой изоляции, накладываемый на поверхность трубы, выполнен из материала с коэффициентом теплопроводности  , второй слой – из материала с коэффициентом теплопроводности
, второй слой – из материала с коэффициентом теплопроводности  .
.
Температура внутренней поверхности трубы  , температура наружной поверхности изоляции
, температура наружной поверхности изоляции 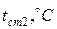 .
.
Определить тепловые потери с единицы длины трубы.

Исходные данные: 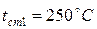 ,
, 
Погонный тепловой поток (тепловой поток на один метр длины трубы) при теплопередаче через трехслойную цилиндрическую стенку определяется по формуле
 ,
,
где 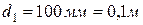 – внутренний диаметр трубы,
– внутренний диаметр трубы,
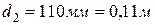 – внешний диаметр трубы,
– внешний диаметр трубы,
 – внешний диаметр первого слоя изоляции,
– внешний диаметр первого слоя изоляции,
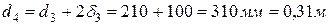 – внешний диаметр второго слоя изоляции,
– внешний диаметр второго слоя изоляции,
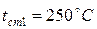 – температура внутренней поверхности трубы,
– температура внутренней поверхности трубы,
 – температура наружного слоя изоляции,
– температура наружного слоя изоляции,
 ,
,  ,
,  – коэффициенты теплопроводности материала стенки трубы и слоев изоляции. Т. е.
– коэффициенты теплопроводности материала стенки трубы и слоев изоляции. Т. е.
 .
.
Т. е. тепловые потери с единицы длины трубы будут равны  .
.
Задача 2 (вариант 1). Плотность теплового потока через плоскую стенку толщиной 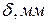 равна
равна 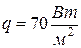 . Определить разность температур на поверхности стенки и численные значения градиента температуры в стенке, если она выполнена:
. Определить разность температур на поверхности стенки и численные значения градиента температуры в стенке, если она выполнена:
а) из латуни  ,
,
б) из красного кирпича  ,
,
в) из пробки 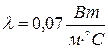 .
.
Исходные данные:  .
.
Плотность теплового потока (количество теплоты, проходящее через единицу площади за единицу времени) через плоскую стенку толщиной  при граничных условиях первого рода определяется по формуле
при граничных условиях первого рода определяется по формуле
 , (1)
, (1)
где  и
и 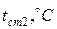 – температуры поверхностей стенки,
– температуры поверхностей стенки, 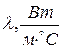 – коэффициент теплопроводности материала стенки,
– коэффициент теплопроводности материала стенки, 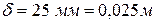 – толщина стенки. Пусть
– толщина стенки. Пусть

– разность температур поверхностей стенки, тогда из равенства 1 получим
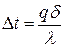 .
.
Для стенки из латуни получим
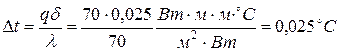 ,
,
для стенки из красного кирпича получим
 ,
,
для стенки из пробки получим
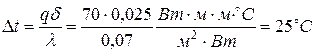 .
.
Согласно закону Фурье плотность теплового потока определяется по формуле
 , (2)
, (2)
где  – градиент температуры. Вектор
– градиент температуры. Вектор  считается положительным, если он направлен в сторону вектора теплового потока
считается положительным, если он направлен в сторону вектора теплового потока 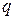 . Поэтому в формуле (2) стоит знак минус. Из равенства (2) получим
. Поэтому в формуле (2) стоит знак минус. Из равенства (2) получим
 .
.
Для стенки из латуни получим
 ,
,
для стенки из красного кирпича получим
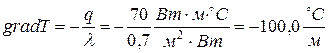 ,
,
для стенки из пробки получим
 .
.
Задача 3 (вариант 2). Определить плотность теплового потока, излучаемого абсолютно черным телом, если его температура 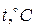 .
.
Исходные данные:  .
.
Плотность лучистого теплового потока абсолютно черного тела определяется законом Стефана-Больцмана по формуле

где
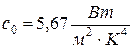 – коэффициент излучения абсолютно черного тела,
– коэффициент излучения абсолютно черного тела,
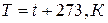 – абсолютная температура тела.
– абсолютная температура тела.
Т. е.
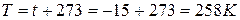 ,
,
 .
.
Задача 4 (вариант 2). Кирпичная стена помещения толщиной в два кирпича ( ), коэффициент теплопроводности которой
), коэффициент теплопроводности которой 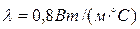 , с внутренней поверхности соприкасается с воздухом, смеющим температуру
, с внутренней поверхности соприкасается с воздухом, смеющим температуру  , коэффициент теплоотдачи к внутренней поверхности стенки
, коэффициент теплоотдачи к внутренней поверхности стенки  . Температура наружного воздуха
. Температура наружного воздуха 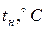 , коэффициент теплоотдачи от наружной поверхности стены, обдуваемой ветром,
, коэффициент теплоотдачи от наружной поверхности стены, обдуваемой ветром,  . Определить плотность теплового потока, уходящего из помещения, а также температуры
. Определить плотность теплового потока, уходящего из помещения, а также температуры 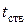 и
и  на поверхности стенки.
на поверхности стенки.
Исходные данные: 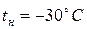 .
.
Коэффициент теплопередачи через плоскую стенку рассчитывается по формуле
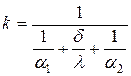 ,
,
т. е.
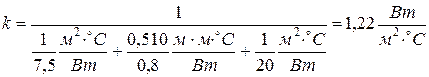
Плотность теплового потока, уходящего из помещения (тепловой поток через единицу площади стенки) определим по формуле
 ,
,
т. е.
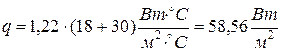 .
.
Температуры стенок найдем по формулам
 ,
,
 ,
,
т. е.
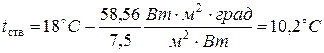 ,
,
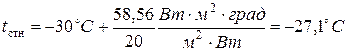 .
.
Задача 5 (вариант 7). Поверхность нагрева парогенератора выполнена из труб с внутренним диаметром 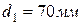 и наружным
и наружным 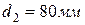 . Температура дымовых газов, омывающих трубу снаружи,
. Температура дымовых газов, омывающих трубу снаружи,  , коэффициент теплоотдачи от газов к наружной поверхности трубы
, коэффициент теплоотдачи от газов к наружной поверхности трубы 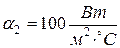 . Температура кипящей воды внутри труб
. Температура кипящей воды внутри труб 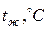 , коэффициент теплоотдачи от внутренней поверхности трубы к воде
, коэффициент теплоотдачи от внутренней поверхности трубы к воде  . Коэффициент теплопроводности материала стенки трубы
. Коэффициент теплопроводности материала стенки трубы 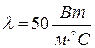 .
.
В процессе эксплуатации поверхность нагрева парогенератора со стороны дымовых газов покрылась слоем сажи толщиной 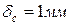 (
( ), и со стороны воды слоем накипи толщиной
), и со стороны воды слоем накипи толщиной 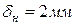 (
( ). Сравнить теплопередачу через чистую стенку трубы и через загрязненную стенку.
). Сравнить теплопередачу через чистую стенку трубы и через загрязненную стенку.
Исходные данные:  ,
, 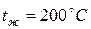 .
.
Коэффициент теплопередачи k через однослойную цилиндрическую стенку определяется по формуле
 ,
,
где  ,
,  – коэффициенты теплоотдачи,
– коэффициенты теплоотдачи,
 – внутренний диаметр трубы,
– внутренний диаметр трубы,
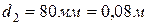 – внешний диаметр трубы,
– внешний диаметр трубы,
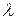 – коэффициент теплопроводности материала стенки.
– коэффициент теплопроводности материала стенки.
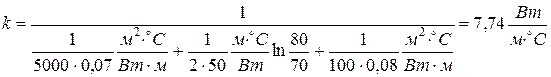 .
.
Погонный тепловой поток при теплопередаче через цилиндрическую стенку определяется по формуле
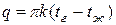 ,
,
т. е. погонный тепловой поток через чистую стенку
 .
.
Коэффициент теплопередачи k через трехслойную цилиндрическую стенку определяется по формуле
 ,
,
где  ,
,  – коэффициенты теплоотдачи,
– коэффициенты теплоотдачи,
 – внутренний диаметр трубы с накипью,
– внутренний диаметр трубы с накипью,
 – внутренний диаметр трубы,
– внутренний диаметр трубы,
 – наружный диаметр трубы,
– наружный диаметр трубы,
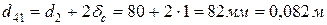 – наружный диаметр трубы с сажей,
– наружный диаметр трубы с сажей,
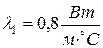 – коэффициент теплопроводности накипи,
– коэффициент теплопроводности накипи,
 – коэффициент теплопроводности материала стенки,
– коэффициент теплопроводности материала стенки,
 – коэффициент теплопроводности сажи.
– коэффициент теплопроводности сажи.

Погонный тепловой поток через загрязненную стенку
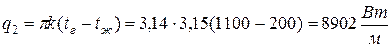 .
.
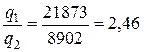 .
.
Теплопередача через загрязненную стенку почти в два с половиной раза меньше сем через чистую стенку.
Задача 6 (вариант 7). К отопительной системе, состоящей из котла, радиаторов, трубопроводов присоединен расширительный сосуд, который служит для аккумулирования объема воды при изменении ее температуры.
Сколько воды дополнительно уйдет в расширительный сосуд  при нагревании воды от
при нагревании воды от  до
до  . Объем воды в системе
. Объем воды в системе 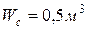 .
.
Исходные данные:  ,
,  .
.
Пусть 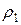 – плотность воды при температуре
– плотность воды при температуре 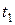 , а
, а 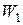 – объем воды в системе при этой температуре. Тогда масса воды в системе
– объем воды в системе при этой температуре. Тогда масса воды в системе
 .
.
Пусть также 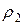 – плотность воды при температуре
– плотность воды при температуре 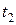 , а
, а  – объем воды в системе при этой температуре. Тогда
– объем воды в системе при этой температуре. Тогда
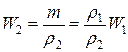 .
.
Объем воды, дополнительно ушедшей в расширительный сосуд, будет равен
 .
.
Плотность воды при температуре  найдем по формуле
найдем по формуле
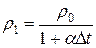 ,
,
где  – плотность воды при температуре
– плотность воды при температуре 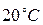 (из прилагаемой таблицы),
(из прилагаемой таблицы), 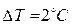 ,
, 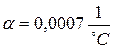 – коэффициент температурного расширения. Т. е.
– коэффициент температурного расширения. Т. е.
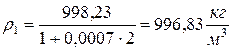 ,
,
а плотность воды при температуре  (из той же таблицы)
(из той же таблицы)
 .
.
Если объем воды в системе при температуре 
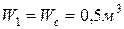
то
 .
.
Масса воды, дополнительно ушедшей в расширительный сосуд, будет равна
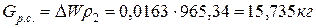 .
.

Задача 7 (вариант 15). Вентиляционная труба диаметром 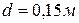 имеет длину
имеет длину  . Определить давление, которое должен развивать вентилятор, если расход воздуха, подаваемый по трубе, составляет
. Определить давление, которое должен развивать вентилятор, если расход воздуха, подаваемый по трубе, составляет  . Шероховатость труб
. Шероховатость труб 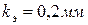 . Давление на выходе атмосферное. Местных сопротивлений по пути не имеется. Температура воздуха
. Давление на выходе атмосферное. Местных сопротивлений по пути не имеется. Температура воздуха 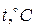 .
.
Исходные данные:  .
.
Сжимаемостью воздуха пренебрегаем. Плотность воздуха при температуре  (из прилагаемой таблицы)
(из прилагаемой таблицы)
 ,
,
его кинематическая вязкость (из той же таблицы)
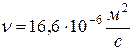 .
.
Скорость потока воздуха найдем через объемный расход  и площадь сечения трубы
и площадь сечения трубы 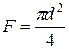
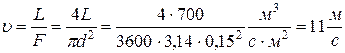 .
.
Найдем число Рейнольдса потока
 .
.
Течение турбулентное (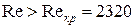 ), Найдем предельные числа Рейнольдса
), Найдем предельные числа Рейнольдса
 ,
, 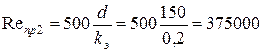 .
.
Так как  , коэффициент гидравлического трения найдем по формуле Альтшуля
, коэффициент гидравлического трения найдем по формуле Альтшуля
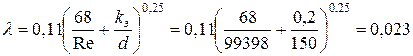 .
.
Потери давления по длине трубопровода найдем по формуле Дарси
 .
.
Будем считать, что труба горизонтальная. Тогда уравнение Бернулли, записанное для двух сечений трубы (выход из вентилятора и выход из трубы) будет иметь вид
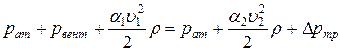 . (1)
. (1)
Здесь  – атмосферное давление,
– атмосферное давление,  – давление, создаваемое вентилятором,
– давление, создаваемое вентилятором, 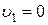 – скорость потока на выходе из вентилятора,
– скорость потока на выходе из вентилятора, 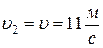 – скорость потока на выходе из трубы,
– скорость потока на выходе из трубы,  и
и  – коэффициенты Кориолиса. Из равенства (1) получим
– коэффициенты Кориолиса. Из равенства (1) получим
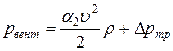 .
.
При турбулентном режиме течения коэффициент Кориолиса 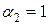 , тогда
, тогда
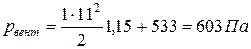 .
.
 Кинематическая вязкость ν*106, м2/с
Кинематическая вязкость ν*106, м2/с
|
Задача 8 (вариант 15). Определить потери давления на трение в стальных воздуховодах круглого, квадратного, треугольного (равносторонний треугольник) сечений при равных длине, площади живого сечения и скорости движения воздуха.
Длина трубы  , температура воздуха
, температура воздуха  , скорость движения
, скорость движения  , площадь сечения
, площадь сечения  , шероховатость труб
, шероховатость труб  .
.
Исходные данные: 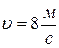 ,
, 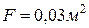 ,
,  .
.
Сжимаемостью воздуха пренебрегаем. Плотность воздуха при температуре  (из прилагаемой таблицы)
(из прилагаемой таблицы)
 ,
,
его кинематическая вязкость (из той же таблицы)
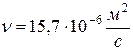 .
.
Рассмотрим трубу круглого сечения. Диаметр трубы найдем через площадь живого сечения
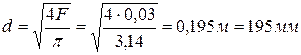 .
.
Найдем число Рейнольдса потока
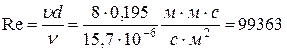 .
.
Течение турбулентное (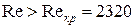 ),Найдем предельные числа Рейнольдса
),Найдем предельные числа Рейнольдса
 ,
, 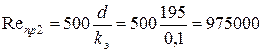 .
.
Так как  , коэффициент гидравлического трения найдем по формуле Альтшуля
, коэффициент гидравлического трения найдем по формуле Альтшуля
 .
.
Потери давления на трении по длине трубопровода найдем по формуле Дарси
 .
.
Рассмотрим трубу квадратного сечения. Сторону квадрата найдем через площадь живого сечения
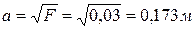 .
.
Смоченный периметр
 ,
,
гидравлический радиус
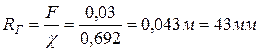 .
.
Найдем число Рейнольдса потока в квадратном канале
 .
.
Течение турбулентное (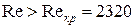 ), Найдем предельные числа Рейнольдса
), Найдем предельные числа Рейнольдса
 ,
, 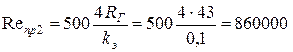 .
.
Так как  , коэффициент гидравлического трения найдем по формуле Альтшуля
, коэффициент гидравлического трения найдем по формуле Альтшуля
 .
.
Потери давления на трении по длине трубопровода найдем по формуле Дарси для некруглых труб
 .
.
Рассмотрим трубу треугольного сечения. Сторону равностороннего треугольника найдем через площадь живого сечения
 .
.
Смоченный периметр
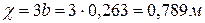 ,
,
гидравлический радиус
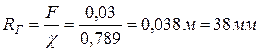 .
.
Найдем число Рейнольдса потока в треугольном канале
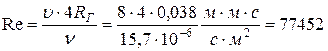 .
.
Течение турбулентное (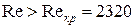 ), Найдем предельные числа Рейнольдса
), Найдем предельные числа Рейнольдса
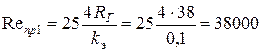 ,
,  .
.
Так как  , коэффициент гидравлического трения найдем по формуле Альтшуля
, коэффициент гидравлического трения найдем по формуле Альтшуля
 .
.
Потери давления на трении по длине трубопровода найдем по формуле Дарси для некруглых труб
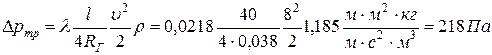 .
.
 Кинематическая вязкость ν*106, м2/с
Кинематическая вязкость ν*106, м2/с
|