Постановка задачи ЛП.
Модель задачи математического программирования включает:
1) Совокупность неизвестных величин Х=(x1, x2, …, xn), действуя на которые, систему можно совершенствовать. Их называют планом задачи;
2) Целевую функцию z(x) [f(x)];
3) Условия (или систему ограничений), налагаемые на неизвестные величины. Эти условия следуют из ограниченности ресурсов, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений.
План Х, удовлетворяющий системе ограничений задачи, называется допустимым.
Допустимый план, доставляющий целевой функции экстремальное значение, называется оптимальным.
Оптимальный план обозначается Х*, а экстремальное значение целевой функции – z(Х*)=z*
Модель задачи ЛП может быть записана в одной из приведённых ниже форм.
1. Общая, или произвольная, форма записи:


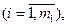

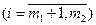


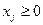

2. Симметричная, или стандартная, форма записи:

 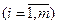
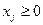 
| 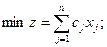
 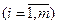
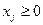 
|
3. Каноническая, или основная, форма записи:


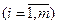
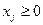

Указанные формы записи ЗЛП эквивалентны, т.е. каждая из них с помощью несложных преобразований может быть сведена к другой форме.
При необходимости задачу минимизации можно заменить задачей максимизации, и наоборот. Очевидно, что минимальное значение функции z(x) равно максимальному значению функции -z(x), взятому с противоположным знаком, т.е.
min z(x)=-max (-z(x))
Неравенство типа ≥ путём умножения левых и правых частей на -1 можно превратить в неравенство типа ≤, и наоборот.
Ограничения – неравенства
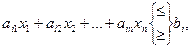
преобразуются в ограничения – равенства путём прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных xn+1≥0:
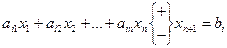 .
.
В случае необходимости ограничение – равенство

можно записать в виде системы неравенств:

Если в ЗЛП какая-то переменная xk не подчинена условию неотрицательности, её заменяют разностью двух других неотрицательных переменных 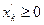 и
и 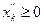 :
:
 .
.
Симплекс – метод
Существует универсальный способ решения задач линейного программирования, называемый симплекс – методом.
Идея симплекс – метода заключается в следующем: сначала надо найти некоторую (начальную) вершину многогранника допустимых решений (начальный опорный план), затем надо проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то надо перейти к другой вершине многогранника и вновь проверить решение на оптимальность. При этом при переходе от одной вершины к другой значение целевой функции убывает (в задаче на min) или возрастает (в задаче на max).
Для построения симплекс – метода решения задач ЛП соответствующие модели должны быть представлены в канонической форме.
Построение начального опорного плана.
1 случай. В системе ограничений имеется единичный неотрицательный базис, т.е. ЗЛП имеет вид:
max z=c1x1+c2x2+…+cnxn;

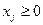
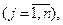

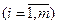
Без ограничения общности можно положить, что базисными являются первые m переменные. Тогда начальный опорный план содержит m базисных и (n-m) свободных переменных. Свободные переменные приравниваются нулю, а базисные – свободным членам. Получаем начальный опорный план 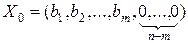
2 случай. Система ограничений имеет вид:
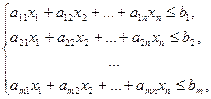



Приводим задачу к каноническому виду, добавляя к левым частям неравенств дополнительные неотрицательные переменные xn+1, xn+2, …, xn+m. Получим систему ограничений

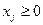
 ,
,
в которой базисными являются переменные xn+1, …, xn+m, а свободными x1, x2, …, xn.
В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю:
z=c1x1+c2x2+…+cnxn+0∙xn+2+…+0∙xn+m
3 случай. Система ограничений имеет вид:
 (1)
(1)



Приводим задачу к каноническому виду, вычитая из левых частей неравенств дополнительные неотрицательные переменные xn+1, xn+2, …, xn+m. Получим систему ограничений:
 , (2)
, (2)
которая не содержит единичного неотрицательного базиса. В этом случае может быть использован искусственный базис. Вводится m искусственных переменных 
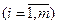 .
.
 (3)
(3)
Искусственные переменные ω1, …, ωm теперь станут базисными, а переменные x1, x2, …, xn+m – свободными.
В целевую функцию z искусственные переменные входят с коэффициентом M со знаком “+”, если эта задача минимизации, и со знаком “-”, если – максимизации. При этом M полагается достаточно большим положительным числом. Т.о. целевая функция имеет вид:
z=c1x1+…+cnxn±Mω1±Mω2±…±Mωm.
Преобразованная подобным образом ЗЛП называется M-задачей.
В оптимальном плане все искусственные переменные ωi должны быть равны нулю, т.к. в исходной задаче таких переменных нет. Дополнительные переменные xn+1, …, xn+m могут иметь положительные значения.
Табличная реализация симплекс – метода
Условия задачи заносятся в таблицу
| A1 A2 An | ||||||
| БП | 
| 
| x1 | x2 | … | xn |
| c1 | c2 | … | cn | |||
| Рабочее поле | ||||||
| Индексные оценки, Δj | Δ0 | Δ1 | Δ2 | … | Δn | |
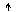 z(x0) z(x0)
|
В столбец БП заносятся базисные переменные.
Столбец СБ содержит коэффициенты целевой функции, стоящие при базисных переменных.
Столбец А0 (базисные значения) содержит значения БП в опорном плане.
Рабочее поле содержит коэффициенты при переменных в ограничениях – равенствах, содержащих соответствующую базисную переменную.
Индексные оценки определяются формулами:

Признак оптимальности опорного плана:
1. если исходная задача на max и для некоторого опорного плана все индексные оценки Δj≥0, то такой план оптимален.
2. если исходная задача на min и для некоторого опорного плана все индексные оценки Δj≤0, то такой план оптимален.
Переход к нехудшему опорному плану.
Если в таблице все Δj≥0 (max) {Δj≤0 (min)}, то начальный опорный план Х0 оптимален. Если же существуют Δj<0 {Δj>0}, то находим среди них (неправильных индексных оценок) максимальную по модулю:

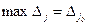
Δj<0
{Δj>0}
Столбец j0 называется разрешающим. Переменную xj0, соответствующую разрешающему столбцу, следует ввести в базис.
Для определения переменной, выводимой из базиса, находят симплексные отношения: для этого делим соответственно элементы A0 на положительные коэффициенты Aj0. Среди симплексных отношений определяют наименьшее; оно и укажет строку, в которой содержится исключаемая из базиса переменная xi0. Строка i0, соответствующая минимальному симплексному отношению, называется разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, также называется разрешающим.
Строим новую симплексную таблицу по правилу:
1. элементы разрешающей i0 -той строки делим на разрешающий элемент;
2. все элементы разрешающего столбца j0 равны нулю (включая Δj0), за исключением 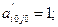
3. столбцы, соответствующие оставшимся БП остаются без изменений;
4. остальные элементы получаем по правилу прямоугольника:
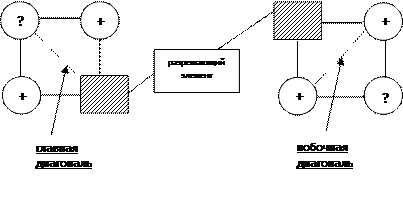 |
Элементы? = (произведению элементов по главной диагонали минус произведение элементов по побочной диагонали), деленному на разрешающий элемент.
Контроль вычислений элементов индексной строки осуществляется по формулам:

Признак неограниченности целевой функции:
Если в разрешающем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена.