| № | Задание | Варианты ответов | ||||||||||||||||||||||||||||||||||||||||
Пусть А и В – множества, изображенные на рисунке.
Тогда объединением этих множеств является:

| 1. Ø 2. А\В 3. В 4. А | |||||||||||||||||||||||||||||||||||||||||
2. Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
A)  B) B)  C) В D) C) В D) 
| A) - B) - C)- D) - | |||||||||||||||||||||||||||||||||||||||||
Пусть  . Тогда множество M1 равно… . Тогда множество M1 равно…
|
1.  2. 2.  3. 3.  4. 4. 
| |||||||||||||||||||||||||||||||||||||||||
| Заданы множества А = { 4,5,6} В = {5, 6,4}. Тогда для них неверным утверждением будет: | 1 Множество А есть подмножество множества В 2.Множества А и В равны 3.Множество А включает в себя множество В 4. Множества А и В не имеют равных элементов | |||||||||||||||||||||||||||||||||||||||||
Даны множества A={ a, b, c, d, e, f} и B={e, f, k}. Установите соответствия между обозначениями множеств и самими множествами. 1. A  B 2. A B 2. A  B 3. A\B 4. B\A B 3. A\B 4. B\A
| A) {a, b, c, d, e, f, k} B) {a, b, c, d} C) {e, f} D) {k} | |||||||||||||||||||||||||||||||||||||||||
Заданы множества  {1,-3} и {1,-3} и  {-а, в}, тогда декартовым произведением этих множеств А´В является множество … {-а, в}, тогда декартовым произведением этих множеств А´В является множество …
| 1. {-а, в, 1, -3} 2. {(-а,1),(в,-3),(в,1),(-а,-3)} 3. {(1,-a), (1, в), (-3,-а), (-3, в)} 4. {  } }
| |||||||||||||||||||||||||||||||||||||||||
Высказывание A – «Ада Лавлейс - графиня»; высказывание В – «Диагонали ромба равны». Дизъюнкцией этих высказываний ( ) является предложение … ) является предложение …
| 1. «Ада Лавлейс – графиня, или диагонали ромба равны» 2. «Если Ада Лавлейс – графиня, то диагонали ромба равны» 3. «Ада Лавлейс – графиня тогдаитолькотогда, когда диагонали ромба равны» 4. «Ада Лавлейс – графиня, и диагонали ромба равны» 1. | |||||||||||||||||||||||||||||||||||||||||
| В слове «RITM» меняют местами буквы. Тогда количество всех возможных различных «слов» равно… | 1. 20 2. 24 3. 4 4. 16 | |||||||||||||||||||||||||||||||||||||||||
| Количество различных двузначных чисел, которые можно составить из цифр:1,2,3,4,5 (все цифры в числе различны) равно: | 1.25 2.32 3.10 4.20 | |||||||||||||||||||||||||||||||||||||||||
| Количество перестановок из букв слова «вальс», в которых буква «в» на первом месте, а буква «с» - в конце слова, равно… | 1. 24 2. 6 3. 5 4. 4 | |||||||||||||||||||||||||||||||||||||||||
| По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,5; при втором - 0,3; при третьем – 0,2; при четвертом – 0,1. Тогда вероятность того, что мишень не будет поражена ни разу равна… | 1. 0,03 2. 0,275 3. 0,003 4. 1,1 | |||||||||||||||||||||||||||||||||||||||||
| Вероятность того, что студент сдаст на «5» первый экзамен равна 0,4, а второй – 0,5. Тогда вероятность того, что студент сдаст на «5» оба экзамена равна: | 1. 0,7 2. 0,9 3. 0,2 4. 0, 4 | |||||||||||||||||||||||||||||||||||||||||
| Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, большее 2, равна … | 1.  3. 3.  2.
2. 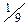 4. 4. 
| |||||||||||||||||||||||||||||||||||||||||
| Вероятности того, что студент сдаст зачет по информатике, экзамен по философии, соответственно равны 0,8 и 0, 6. Какова вероятность того, что студент сдаст все? | 1. 0,92 2. 0,72 3. 0,5 4. 0,48 | |||||||||||||||||||||||||||||||||||||||||
Дискретная случайная величина Х имеет закон распределения вероятностей:
Тогда математическое ожидание М(Х) этой случайной величины равно: | 1. 1 2. 3,2 3. 7 4. 3,8 | |||||||||||||||||||||||||||||||||||||||||
| Вероятность наступления некоторого события не может быть равна: | 1. 0,7 2. 0 3.2,5 4.0,1 | |||||||||||||||||||||||||||||||||||||||||
| График плотности вероятностей для нормального распределения изображен на рисунке... | 1.  2. 2. 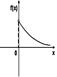 3.
3.  4. 4. 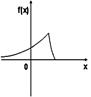
| |||||||||||||||||||||||||||||||||||||||||
| Два стрелка независимо друг от друга делают по одному выстрелу по цели. Вероятность попадания в цель первого стрелка –0,7, второго – 0,8. Найти вероятность того, что только один стрелок попадет в цель. | 1. 0,56 2. 0,7 3. 0,38 4. 0,8 | |||||||||||||||||||||||||||||||||||||||||
| В результате 10 опытов получена следующая выборка: 2,5,7,7,5,2,4,4,5,5 Тогда для нее законом распределения будет: | 1.
2.
3.
4.
| |||||||||||||||||||||||||||||||||||||||||
| Средняя выборочная вариационного ряда 3, 2, 7, 5, 2 равна: | 1. 4,2 2. 3,6 3. 5 4. 3,8 | |||||||||||||||||||||||||||||||||||||||||
Статистическое распределение выборки
имеет вид:
Тогда объем выборки: | 1.3 2.16 3. 14 4. 6 | |||||||||||||||||||||||||||||||||||||||||
| Медиана вариационного ряда 5,3,5,7,9,6,7,2,3 равна: | 1. 3 2. 7 3. 5 4. 6 | |||||||||||||||||||||||||||||||||||||||||
| Мода вариационного ряда: 5,3,5,7,9,7,7,2,3 равна: | 1. 5 2. 7 3. 3 4. 9 | |||||||||||||||||||||||||||||||||||||||||
Из генеральной совокупности извлечена выборка объема n=60, полигон частот которой имеет вид:
 Тогда число вариант
Тогда число вариант 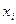 =3 в выборке равно: =3 в выборке равно:
| 1. 9 2. 10 3. 12 4. 11 | |||||||||||||||||||||||||||||||||||||||||
Отношение задано неравенством 4х-2у  0. тогда данному отношению принадлежит следующая пара чисел: 0. тогда данному отношению принадлежит следующая пара чисел:
| 1. (-1; 0) 2. (1; 1) 3. (0; 1) 4. (-1; -1) |

Вариант 2.
| № | Задание | Варианты ответов | ||||||||||||||||||||||||||||||||||||||||
Пусть А и В – множества, изображенные на рисунке.
Тогда объединением этих множеств является:

| 1. Ø 2. А 3. В\А 4. В | |||||||||||||||||||||||||||||||||||||||||
| На факультете культуры учатся студенты, знающие иностранный язык; при этом есть студенты, знающие два иностранных языка. Пусть А – множество всех студентов факультета; В – множество студентов факультета, которые знают два иностранных языка. Тогда пересечением этих множеств будет: | 1.Множество всех студентов факультета 2.Множество студентов факультета, не знающих иностранного языка 3. Множество студентов факультета, знающих два иностранных языка 4. Ø | |||||||||||||||||||||||||||||||||||||||||
| Заданы множества С = {1,2,3} D = {3,2,1}.тогда для них неверным утверждением будет: | 1. Множество C есть подмножество множества D 2. Множества C и D равны 3. Множество C не равно множеству D 4. Множество D есть подмножество множества С | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество Z – все целые числа; множество N –натуральные числа. Тогда разностью множеств Z и N будет: | 1. Все натуральные числа 2.Числа, противоположные натуральным 3. Числа, противоположные натуральным и число 0 4. Целые числа | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А = { 2,8,15} В = {8, 9, 12, 15} Тогда разностью множеств А \ В будет: | 1.А \ В={ 2,8,9} 2.А\В={8, 9, 12,15} 3. А \ В={ 2} 4.А \ В={ 9,12} | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А =[ -10; 8); В = (-2; 15] Тогда разностью множеств В \ А будет: | 1.В \ А= [ -10; -2); 2.В \ А=(8; 15] 3.В \ А= [ 8; 15] 4.В \ А=[ -10; -2]; | |||||||||||||||||||||||||||||||||||||||||
| В слове «PUSK» меняют местами буквы. Тогда количество всех возможных различных «слов» равно: | 1. 16 2. 8 3. 24 4. 4 | |||||||||||||||||||||||||||||||||||||||||
| Количество различных способов выбора (порядок не имеет значения) 10 томов из 12-томного собрания сочинений Р.Гари равно: | 1. 132 2. 120 3. 66 4. 22 | |||||||||||||||||||||||||||||||||||||||||
| Для выпускников юридического факультета предоставили 3 вакансии на должность помощника адвоката. Изъявили желание занять одно из этих мест 20 выпускников. Сколькими способами эти вакансии могут быть распределены между 20–ю выпускниками? | 1. 60
2. 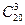 3.
3.  4. 20!
4. 20!
| |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами можно выбрать из 15 мужчин и 18 женщин группу из 5 мужчин и 8 женщин? | 1. 5  8
2. 8
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||
| Количество различных трехбуквенных комбинаций, которые можно составить из букв слова «ГРОМ» (все буквы в комбинации различны), равно: | 1. 81 2. 12 3. 64 4. 24 | |||||||||||||||||||||||||||||||||||||||||
| Из сотрудников 4-х юридических фирм нужно составить выездную группу из 5–ти человек. Сколькими способами можно это сделать? | 1.  2.
2.  3. 5* 4
4. 5!
3. 5* 4
4. 5!
| |||||||||||||||||||||||||||||||||||||||||
| В результате 10 опытов получена следующая выборка: 2,3, 6,6, 4,4, 6,6, 3,4. Тогда для нее законом распределения будет: | 1.
2.
3.
4.
| |||||||||||||||||||||||||||||||||||||||||
| Средняя выборочная вариационного ряда 1, 3, 3, 2,1 равна: | 1. 3 2. 2 3. 2,5 4. 5 | |||||||||||||||||||||||||||||||||||||||||
Статистическое распределение выборки
имеет вид:
Тогда объем выборки: | 1. 11 2. 20 3. 10 4. 18 | |||||||||||||||||||||||||||||||||||||||||
| Медиана вариационного ряда 2,5,4,2,3,6,5,5, 2 равна: | 1. 3 2. 4 3. 5 4. 6 | |||||||||||||||||||||||||||||||||||||||||
| Мода вариационного ряда: 2,5,5,2,3,6,5,5, 2 равна: | 1. 3 2. 2 3. 5 4. 6. | |||||||||||||||||||||||||||||||||||||||||
Из генеральной совокупности извлечена выборка объема n=35, полигон частот которой имеет вид:
 Тогда число вариант
Тогда число вариант 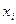 =4 в выборке равно: =4 в выборке равно:
| 1. 5 2. 20 3. 7 4. 8 | |||||||||||||||||||||||||||||||||||||||||
| Петя сдаст экзамен на отлично с вероятностью 0,9, а Вася – с вероятностью 0,1. Тогда вероятность того, что оба они сдадут экзамен на отлично, равна: | 1. 1 2. 0,09 3. 0,91 4. 0,9 | |||||||||||||||||||||||||||||||||||||||||
| Студент бросает в окно бумажные самолетики. Вероятность того, что первый самолетик попадет в окно – 0, 3, а второй – 0, 4. Какова вероятность того, что хотя бы один из самолетиков попадет в окно? | 1. 0,88 2. 0,58 3. 0,12 4. 0,5 | |||||||||||||||||||||||||||||||||||||||||
| Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков меньше, чем три, равна: | 1. 1 2. ½ 3. 1/36 4. 1/3 | |||||||||||||||||||||||||||||||||||||||||
Дискретная случайная величина Х имеет закон распределения вероятностей:
Тогда математическое ожидание М(Х) этой случайной величины равно:
| 1. 1 2. 8 3. 3,8 4. 4,2 | |||||||||||||||||||||||||||||||||||||||||
| В урне 8 красных и 5 синих шаров. Вынимаются друг за другом 2шара. Найти вероятность того, что оба шара окажутся красными. | 1. 14/39 2. 1/64 3. 1/40 4. 5/39 | |||||||||||||||||||||||||||||||||||||||||
| В ящике 5 качественных и 5 бракованных изделий. Опыт состоит в выборе только одного изделия. Событие А – «Вынули качественное изделие.» Событие В – «Вынули бракованное изделие». Тогда для этих событий верным будет утверждение: | 1. События А и В равновероятны 2. Событие А достоверно 3. Событие В невозможно 4. Вероятность события В больше вероятности события А | |||||||||||||||||||||||||||||||||||||||||
| Установите правильное соответствие между математическим утверждением и его формулировкой. 1. «Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом» 2. «Из трех точек прямой одна и только одна лежит между двумя другими» 3. «Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны» | О Аксиома О Теорема О Определение |
Вариант 3.
| № | Задание | Варианты ответов | ||||||||||||||||||||||||||||||||||||||||
Пусть А и В – множества, изображенные на рисунке.
Тогда объединением этих множеств является:

| 1. Ø 2. В 3. В\А 4. А | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А – все студенты, обучающиеся в Университете (в Университете есть несколько факультетов); множество В – студенты, обучающиеся на экономическом факультете. Тогда пересечением множеств А и В будет: | 1.Все студенты Университета 2.Студенты, обучающиеся на экономическом факультете 3.Студенты, не обучающиеся на экономическом факультете 4. Ø | |||||||||||||||||||||||||||||||||||||||||
| Заданы множества В = {3,4, 5, 6} С = {3,6}. Тогда для них верным утверждением будет: | 1.Множество В есть подмножество множества С 2. Множества В и С равны 3. Множество С есть подмножество множества В 4.Множества В и С не имеют одинаковых элементов | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество В – все четырехугольники; множество А – все параллелограммы. Тогда пересечением множеств В и А будет: | 1. Множество всех четырехугольников 2. Множество всех параллелограммов 3. Множество четырехугольников, отличных от паралле- лограммов 4. Ø | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А = { 3,5,9} В = {4, 7, 9, 15} Тогда разностью множеств В\А будет: | 1. В\А ={ 3,5,9} 2.В\А ={4, 7, 15} 3. В\А ={ 3, 5} 4. В\А ={ 9,15} | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А =[ -13;7]; В = (-2; 10) Тогда разностью множеств А\В будет: | 1. А\В = [ -13;-2); 2. А\В =(7; 10) 3. А\В = [ -13;-2] 4. А\В =[ 7; 10]; | |||||||||||||||||||||||||||||||||||||||||
| Количество перестановок букв в слове «план» равно: | 1.24 2.120 3.20 4.50 | |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами можно выбрать трех докладчиков на собрании из группы в 20 человек? | 1. 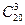 2.
2.  3. 3*20
4. 20!
3. 3*20
4. 20!
| |||||||||||||||||||||||||||||||||||||||||
| Есть три вакансии на должности: следователя, помощника адвоката и прокурора. Сколькими способами можно распределить эти вакансии между 18 претендентами? | 1.  2.
2.  3. 18*3
4. 18!
3. 18*3
4. 18!
| |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами можно выбрать из 10 красных и 8 синих шариков набор из 5 красных и 4 синих шариков? | 1. 5  4
2. 4
2.  3.
3.  4.
4. 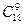
| |||||||||||||||||||||||||||||||||||||||||
| Сколько различных трехзначных чисел можно составить из цифр 0,1,2,3,4, при условии, что цифры не должны повторяться? | 1. 3*4² 2. 4³ 3. 5! 4. 5*5*5 | |||||||||||||||||||||||||||||||||||||||||
| Количество различных трехбуквенных комбинаций, которые можно составить из букв слова «минута» (все буквы в комбинации различны), равно: | 1. 240 2. 6 3. 120 4. 20 | |||||||||||||||||||||||||||||||||||||||||
| Студент на экзамене верно ответит на первый вопрос с вероятностью 0,8, на второй вопрос – с вероятностью 0,6. Тогда вероятность того, что он верно ответит на оба вопроса, равна: равна: | 1. 1,4 2. 0,6 3. 0,2 4. 0,48 | |||||||||||||||||||||||||||||||||||||||||
| Игральный кубик бросается один раз. Тогда вероятность того, что на верхней грани выпадет число очков, меньшее, чем 4, равна: | 1. 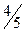 2.
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||
| Из числа талонов, занумерованных двузначными числами, наугад берется один. Какова вероятность того, что номер взятого талона не содержит цифры 3? | 1. 0,53 2. 0,8 3. 0,81 4. 0,4 | |||||||||||||||||||||||||||||||||||||||||
Дискретная случайная величина Х имеет закон распределения вероятностей:
Тогда математическое ожидание М(Х) этой случайной величины равно:
| 1. 0,8 2. 1,6 3. 0,5 4. 0.6 | |||||||||||||||||||||||||||||||||||||||||
| В корзине 6 спелых и 4 неспелых апельсина. Какова вероятность того, что вынутых друг за другом два апельсина окажутся неспелыми? | 1. 0,15 2. 0,14 3. 0,13 4. 0,33 | |||||||||||||||||||||||||||||||||||||||||
| Два орудия делают выстрел по мишени. Вероятность попадания в мишень для каждого орудия соответственно равна 0,7 и 0,8. Найти вероятность того, что произойдет хотя бы одно попадание в мишень. | 1. 0,44 2. 0,92 3. 0,94 4. 0,56 | |||||||||||||||||||||||||||||||||||||||||
| В результате 10 опытов получена следующая выборка: 2,2,4,4,5,4,7,5,7,5 Тогда для нее законом распределения будет: | 1.
2.
3.
4.
| |||||||||||||||||||||||||||||||||||||||||
| Средняя выборочная вариационного ряда 3,3,4,4,5 равна: | 1. 3,8 2. 3,5 3. 3,4 4. 4,25 | |||||||||||||||||||||||||||||||||||||||||
Статистическое распределение выборки
имеет вид:
Тогда объем выборки: | 1.16 2.18 3. 14 4. 63 | |||||||||||||||||||||||||||||||||||||||||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза: , то конкурирующей может быть гипотеза:
| 1. 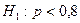 ,
2. ,
2.  ,
3. ,
3.  ,
4. ,
4.  , ,
| |||||||||||||||||||||||||||||||||||||||||
| Мода вариационного ряда: 5,4,6,7,5,7,4,5,7,7 равна: | 1. 4 2. 5 3. 7 4. 6 | |||||||||||||||||||||||||||||||||||||||||
Из генеральной совокупности извлечена выборка объема n=50, полигон частот которой имеет вид:
 Тогда число вариант
Тогда число вариант 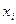 =4 в выборке равно: =4 в выборке равно:
| 1. 19 2. 18 3. 17 4. 16 | |||||||||||||||||||||||||||||||||||||||||
Отношение задано неравенством 3х-4у  0, тогда данному отношению принадлежит следующая пара чисел: 0, тогда данному отношению принадлежит следующая пара чисел:
| 1. (2;0) 2. (3;1) 3. (1;0) 4. (0;1) | |||||||||||||||||||||||||||||||||||||||||
Вариант 4.
| № | Задание | Варианты ответов | ||||||||||||||||||||||||||||||||||||||||
Пусть А и В – множества, изображенные на рисунке.
Тогда пересечением этих множеств является:

| 1. Ø 2. В 3. В\А 4. А | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А – все студенты, обучающиеся в Университете (среди них есть обучающиеся платно и бесплатно); множество В – студенты, обучающиеся платно. Тогда разностью множеств А и В будет: | 1.Все студенты Университета 2.Студенты, обучающиеся платно 3.Студенты, обучающиеся бесплатно 4. Ø | |||||||||||||||||||||||||||||||||||||||||
Пусть А и В – множества, изображенные на рисунке.
Тогда объединением этих множеств является:
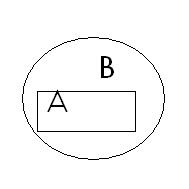
| 1. Ø 2. В 3. В\А 4. А | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество N – все натуральные числа; множество В –натуральные числа, кратные трем.. Тогда пересечением множеств N и В будет: | 1. Все натураль-ные числа 2.Натуральные числа, кратные трем 3.Натуральные числа, не кратные трем 4. Ø | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А = { 3,5,7} В = {5, 7, 9, 11} Тогда разностью множеств А \ В будет: | 1.А \ В={ 3,5,7} 2.А\В={5, 7, 9, 11} 3. А \ В={ 3} 4.А \ В={ 9,11} | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А =[ -12; 6); В = (0; 8] Тогда разностью множеств В \ А будет: | 1.В \ А= [ -12; 0); 2.В \ А=(6; 8] 3.В \ А= [ 6; 8] 4.В \ А=[ -12; 0]; | |||||||||||||||||||||||||||||||||||||||||
| Количество перестановок букв в слове «точка» равно: | 5. 24 6. 120 7. 10 8. 20 | |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами 9 юношей могут пригласить на танец 9 девушек? | 1.9! 2.81 3.18 4.36 | |||||||||||||||||||||||||||||||||||||||||
| Менеджер рассматривает кандидатуры 8 человек, подавших заявления о приеме на работу. Сколько существует способов приглашения кандидатов на собеседование в случайном порядке? | 2. 8 3. 8! 4. 36 5. 64 | |||||||||||||||||||||||||||||||||||||||||
| В группе во втором семестре 10 предметов и 3 пары различных занятий в день. Сколькими способами можно составить расписание занятий для группы на один день? | 1. 10  3
2. 3
2.  3.
3.  4. 60
4. 60
| |||||||||||||||||||||||||||||||||||||||||
| Сколько различных трехзначных чисел можно составить из цифр 1,2,3,4,5 при условии, что каждая цифра в обозначении числа встречается один раз? | 1.  2. 5!
3.
2. 5!
3.  4.
4. 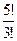
| |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами группу из 20 человек можно разбить на 2 подгруппы? | 1.  2.
2.  3. 20 * 2
4.
3. 20 * 2
4. 
| |||||||||||||||||||||||||||||||||||||||||
| Вероятность того, что студент сдаст на «5» первый экзамен равна 0,6, а второй – 0,3. Тогда вероятность того, что студент сдаст на «5» оба экзамена равна: | 1. 0,16 2. 0,9 3. 0,24 4. 0,18 | |||||||||||||||||||||||||||||||||||||||||
| Игральный кубик бросается один раз. Тогда вероятность того, что на верхней грани выпадет четное число очков, равна: | 1.  2. 2.  3.
3.  4. 4. 
| |||||||||||||||||||||||||||||||||||||||||
| Из числа талонов, занумерованных двузначными числами, наугад берется один. Какова вероятность того, что номер взятого талона не содержит цифры 7? | 5. 0,53 6. 0,72 7. 0,81 8. 0,49 | |||||||||||||||||||||||||||||||||||||||||
Дискретная случайная величина Х имеет закон распределения вероятностей:
Тогда математическое ожидание М(Х) этой случайной величины равно:
| 5. 1 6. 0,2 7. 1,4 8. 2 | |||||||||||||||||||||||||||||||||||||||||
| В урне 7 белых и 3 красных шара. Наудачу вынимаются 2 из них. Найти вероятность того, что оба шара окажутся красными. | 1. 2/3 2. 1/15 3.1/5 4.1/21 | |||||||||||||||||||||||||||||||||||||||||
| Два стрелка независимо друг от друга делают по одному выстрелу по цели. Вероятность попадания в цель первого стрелка – 0,5, второго – 0,75. Найти вероятность того, что только один стрелок попадет в цель. | 5. 0,5 6. 0,7 7. 0,65 8. 0,75 | |||||||||||||||||||||||||||||||||||||||||
| В результате 10 опытов получена следующая выборка: 2,2,3,3.3,4,4,4,5,5 Тогда для нее законом распределения будет: | 1.
2.
3.
4.
| |||||||||||||||||||||||||||||||||||||||||
| Средняя выборочная вариационного ряда 1, 2, 5. 3, 2 равна: | 5. 6 6. 2,6 7. 5 8. 3,1 | |||||||||||||||||||||||||||||||||||||||||
Статистическое распределение выборки
имеет вид:
Тогда объем выборки: | 1.18 2.20 3. 11 4. 10 | |||||||||||||||||||||||||||||||||||||||||
| Медиана вариационного ряда 3,4,5,2,5.6.4,5, 4 равна: | 5. 3 6. 4 7. 5 8. 6 | |||||||||||||||||||||||||||||||||||||||||
| Мода вариационного ряда: 3,2,3,4,3,5,6,4,2 равна: | 5. 3 3. 2 6. 4 4. 5 | |||||||||||||||||||||||||||||||||||||||||
Из генеральной совокупности извлечена выборка объема n=60, полигон частот которой имеет вид:
 Тогда число вариант
Тогда число вариант 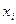 =4 в выборке равно: =4 в выборке равно:
| 5. 9 6. 10 7. 12 8. 11 | |||||||||||||||||||||||||||||||||||||||||
| К неопределяемым понятиям аксиоматического построения геометрии относятся: | 1. фигура, плоскость, отрезок 2. точка, прямая, плоскость 3. луч, отрезок, угол 4.точка, множество, треугольник |
Вариант 5.
| № | Задание | Варианты ответов | ||||||||||||||||||||||||||||||||||||||||
Пусть А и В – множества, изображенные на рисунке.
Тогда объединением этих множеств является:

| 1. Ø 2. В 3. В\А 4. А | |||||||||||||||||||||||||||||||||||||||||
| На факультете учатся студенты, имеющие домашний персональный компьютер и студенты, не имеющие домашнего персонального компьютера. Пусть А – множество всех студентов факультета; В – множество студентов факультета, имеющих домашний персональный компьютер. Тогда разностью (А\В) этих множеств будет: | 1.Множество всех студентов факультета 2.Множество студентов факультета, не имеющих домашнего перс. компьютера 3. Множество студентов факультета, имеющих домашний перс. компьютер 4. Ø | |||||||||||||||||||||||||||||||||||||||||
| Заданы множества А = {4,5,6} В = {6,5,4}.тогда для них неверным утверждением будет: | 5. Множество А есть подмножест-во множества В 2. Множества А и В равны 3. Множество А включает в себя множество В 4. Множества А и В не имеют общих элементов | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество N – все натуральные числа; множество В –натуральные числа, кратные трем.. Тогда разностью множеств N и В будет: | 1. Все натураль-ные числа 2.Натуральные числа, кратные трем 3.Натуральные числа, не кратные трем 4. Ø | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А = { 2,6,12} В = {6, 7, 9, 12} Тогда разностью множеств А \ В будет: | 1.А \ В={ 2,6,7} 2.А\В={6, 7, 9, 12} 3. А \ В={ 2} 4.А \ В={ 9,12} | |||||||||||||||||||||||||||||||||||||||||
| Пусть множество А =[ -18; 4); В = (0; 10] Тогда разностью множеств В \ А будет: | 1.В \ А= [ -18; 0); 2.В \ А=(4; 10] 3.В \ А= [ 4; 10] 4.В \ А=[ -18; 0]; | |||||||||||||||||||||||||||||||||||||||||
| Количество перестановок букв в слове «число» равно: | 9. 24 10. 120 11. 10 12. 20 | |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами можно расставить на полке 10 томное собрание сочинений? | 1.10! 2.100 3.20 4.5! | |||||||||||||||||||||||||||||||||||||||||
| Менеджер рассматривает кандидатуры 6 человек, подавших заявления о приеме на работу. Сколько существует способов приглашения кандидатов на собеседование в случайном порядке? | 6. 6 7. 6! 8. 36 9. 48 | |||||||||||||||||||||||||||||||||||||||||
| Сколькими способами можно выбрать из 10 мужчин и 15 женщин группу из 3 мужчин и 5 женщин? | 1. 5  3
2. 3
2.  3.
3.  4.
4. 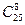
| |||||||||||||||||||||||||||||||||||||||||
| Сколько различных трехзначных чисел можно составить из цифр 1,3,5,7,9 при условии, что каждая цифра в обозначении числа встречается один раз? | 1.  2. 5!
3.
2. 5!
3.  4.
4. 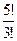
| |||||||||||||||||||||||||||||||||||||||||
| Сколько различных способов заполнения карточки «Спортлото» (6 из 49)? | 1.  2.
2.  3. 49 * 6
4. 6!
3. 49 * 6
4. 6!
| |||||||||||||||||||||||||||||||||||||||||
| В результате 10 опытов получена следующая выборка: 2,2,2,3.3,4,4,4,6,6 Тогда для нее законом распределения будет: | 1.
2.
3.
4.
| |||||||||||||||||||||||||||||||||||||||||
| Средняя выборочная вариационного ряда 2, 3, 4. 4, 5 равна: | 5. 2,8 3. 3,5 6. 4,5 4. 3,6 | |||||||||||||||||||||||||||||||||||||||||
Статистическое распределение выборки
имеет вид:
Тогда объем выборки: | 1. 26 2. 35 3. 14 4. 16 | |||||||||||||||||||||||||||||||||||||||||
| Медиана вариационного ряда 3,5,6,2,3.6.5,5, 2 равна: | 5. 3 3. 4 6. 5 4. 6 | |||||||||||||||||||||||||||||||||||||||||
| Мода вариационного ряда: 3,5,6,2,3,6,5,5,2 равна: | 5. 3 6. 4 7. 5 8. 6. | |||||||||||||||||||||||||||||||||||||||||
Из генеральной совокупности извлечена выборка объема n=60, полигон частот которой имеет вид:
 Тогда число вариант
Тогда число вариант 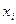 =3 в выборке равно: =3 в выборке равно:
| 5. 27 6. 25 7. 60 8. 26 | |||||||||||||||||||||||||||||||||||||||||
| Вероятность того, что студент сдаст на «5» первый экзамен равна 0,5, а второй – 0,4. Тогда вероятность того, что студент сдаст на «5» оба экзамена равна: | 1. 0,2 2. 0,9 3. 0,24 4. 0,18 | |||||||||||||||||||||||||||||||||||||||||
| Игральный кубик бросается один раз. Тогда вероятность того, что на верхней грани выпадет число очков меньше, чем 4, равна: | 1. 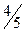 2.
2.  3.
3.  4.
4. 
| |||||||||||||||||||||||||||||||||||||||||
| Из 40 экзаменационных вопросов студент выучил 30. Какова вероятность того, что он ответит на 3 заданных вопроса? | 5. 0,44 6. 0,441 7. 0,39 8. 0,5 | |||||||||||||||||||||||||||||||||||||||||
Дискретная случайная величина Х имеет закон распределения вероятностей:
Тогда математическое ожидание М(Х) этой случайной величины равно:
| 5. 3,2 6. 1 7. 7 8. 3,8 | |||||||||||||||||||||||||||||||||||||||||
| В урне 7 белых и 5 черных шаров. Вынимаются друг за другом 2шара. Найти вероятность того, что оба шара окажутся черными. | 1. 5/33 2. 1/10 3. 1/2 4. 2/5 | |||||||||||||||||||||||||||||||||||||||||
| В коробке 10 качественных и 4 бракованных прибора. Опыт состоит в выборе только одного прибора. Событие А – «Вынули качественный прибор.» Событие В – «Вынули бракованный прибор». Тогда для этих событий неверным будет утверждение: | 1.Вероятность события В = 2/7 2. События А и В несовместны 3.Вероятность события А = 5/7 4. Вероятность события А = вероятности события В. | |||||||||||||||||||||||||||||||||||||||||
| Установите правильное соответствие между математическим утверждением и его формулировкой. 4. «Треугольник, у которого все три угла острые, называется остроугольным» 5. «Имеются по крайней мере четыре различных точки, не лежащие в одной плоскости» 6. «Если при пересечении двух прямых секущей, сумма односторонних углов равна 180 º, то прямые параллельны» | О Аксиома О Теорема О Определение | |||||||||||||||||||||||||||||||||||||||||
Вариант 6.
| № | Задание | Варианты ответов | ||
Пусть А и В – множества, изображенные на рисунке.
Тогда пересечением этих множеств является:

| 1. Ø 2. В 3. В\А 4. А | |||
Пусть множество А – все ст
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-11 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |

