Число и его расширение.
Число - важнейшее математическое понятие. Понятие числа изменялось на протяжении веков, постепенно расширяясь, требуя количественные описания и исследования. Проследим все этапы возникновения, развития и расширения числа.
Понятие натурального числа, вызванное потребностью счёта предметов, возникло ещё в доисторические времена. С развитием письменности число стали обозначать знаками. Важным шагом в развитии понятия натурального числа является осознание бесконечности натурального ряда чисел, т. е. безграничного продолжения.
Дальнейшее развитие понятия числа влечёт введение действий над числами. Действия сложения и вычитания возникли по – видимому как объединения двух совокупностей в одну и отделения части совокупности. Умножение возникло в результате счёта равными частями, деление как деление на равные части. Возникает наука о числах – арифметика. Начинается детализация понятия натурального числа, выделяются классы чётных и нечётных чисел, простых и составных и т. д.
Изучение закономерностей в натуральном ряду чисел продолжается и составляет раздел математики, носящий название теория чисел.
Исторически первым расширением понятия числа является присоединение к натуральным числам дробных чисел.
Введение дробных чисел связано с потребностью производить измерения. Измеряется длина посредством откладывания отрезка, принятого за единицу измерения. Например, количество жидкости – при помощи мерного сосуда и т. д. Однако не всегда единица измерения укладывается на измеряемой величине целое число раз. Здесь и содержится источник происхождения наиболее простых и «удобных» дробей, таких как половина, треть, четверть. Созревает идея рассмотрения дробей с любым натуральным знаменателем и представление о дробном числе как о частном при делении двух натуральных чисел, из которых делимое не делится нацело на делитель.
Следующее расширение понятие числа явилось следствием развития математики. Введение отрицательных чисел было вызвано развитием алгебры как науки, дающей общие способы решения арифметических задач. Необходимость введения в алгебру отрицательных чисел возникает уже при решении задач, сводящихся к линейным с одним неизвестным. Широкое использование алгебраических методов для решения задач затруднительно без использования отрицательных чисел. В Индии ещё в VI - XI веках отрицательные числа систематически применялись при решении задач и истолковывались в основном также, как это делается в настоящее время. В Европе эти числа вошли в употребление лишь во времена Р. Декарта. Появление отрицательных чисел приводило и к довольно парадоксальным ситуациям. Скажите, пожалуйста, какое число вдвое больше, чем – 4? Многие мгновенно отвечают: «Минус восемь». А разве - 8 больше чем – 4? В ответ на это возражение обычно говорят: «Тогда минус два». Но, подумав, отказываются и от такого ответа. Какой же ответ верен? Никакой! Всё дело в том, что понятие «вдвое больше» определялось лишь для положительных чисел, а для отрицательных его нужно либо определить заново, либо вообще не использовать. Конечно же, отрицательные числа прибавили забот математикам. Пришлось вводить новые ограничения. Так, запрещались отрицательные числа под знаками квадратного корня и логарифма. И всё же, когда говорят, что нельзя извлечь квадратный корень из отрицательного числа, а также найти логарифм отрицательного числа, делают большую ошибку. Высшая математика учит, что такие корни и логарифмы существуют. Правда, они являются уже недействительными, а комплексными числами.
Числа целые, дробные (положительные и отрицательные) и нуль получили общее название рациональных чисел. В сокровищнице занимательного математического фольклора есть такая задача: «Бутылка с пробкой стоит 11 монет, причём бутылка на 10 монет дороже пробки. Сколько стоит пробка?» Прелесть этой задачи в том, что, недолго думая, все дают ответ: «Пробка стоит 1 монету». И, конечно же, ошибаются! Некоторые, сделав проверку и убедившись в своей ошибке, тут же заявляют, что задача вовсе не имеет решения. Действительно, эта задача не решается в целых числах, но зато существуют дробные числа, подходящие для её решения: десять с половиной монет стоит бутылка, и пол монеты стоит пробка. В древности к целым и дробным числам относились по – разному: предпочтения были на стороне целых чисел. Но хотя Пифагор, со священным трепетом относившийся к натуральным числам, создавая теорию музыкальной шкалы, связал основные музыкальные интервалы с дробями. Правда, самим понятием дроби Пифагор и его ученики не пользовались. Они позволяли себе говорить лишь об отношениях целых чисел. Тем примечательнее. Что один из первых известных нам математических трудов начинался именно с упражнений на действие с дробями. Английский просветитель Джон Керси в предисловии к 16 изданию «Арифметики». Рациональные числа обладают свойствами замкнутости и плотности. Свойство замкнутости заключается в том, что сумма, разность, произведение и частное любых двух рациональных чисел являются снова рациональным числом. Свойства плотности означает, что между любыми двумя различными рациональными числами находится бесконечно много рациональных чисел. Кроме этого совокупность рациональных чисел упорядочено в отношении понятий «больше» и «меньше». Таким образом, введение отрицательных чисел оказалось достаточно для удовлетворения многих практических потребностей, но недостаточным для изучения непрерывно меняющихся переменных величин. Появилось необходимость нового расширения понятия числа, которое состояло в переходе от множества рациональных чисел к множеству действительных чисел. Этот переход состоит в присоединении к рациональным числам так называемых иррациональных чисел. Ещё в Древней Греции было сделано важное открытие: не всегда длина отрезка может быть выражена рациональным числом, если за единицу принят другой отрезок. Появилось понятие несоизмеримости отрезков. Примером несоизмеримости отрезков является сторона квадрата и его диагональ. Диагональ разбивает квадрат на два одинаковых прямоугольных треугольника, в каждом из которых она выполняет роль гипотенузы. Поэтому, как следует из теоремы Пифагора, длина диагонали квадрата равна
1 + 1 =2. Сразу же возникает соблазн достать микрокалькулятор и нажать клавишу извлечения квадратного корня. На табло мы увидим 1, 4142135. Более совершенный калькулятор, выполняющий вычисления с высокой точностью, покажет 1, 414213562373. А с помощью мощного современного компьютера 2 можно вычислить с точностью до сотен, тысяч, миллионов знаков после запятой. Но даже самый высокопроизводительный компьютер, сколь бы долго он не работал, никогда не сможет ни рассчитать все десятичные цифры числа 2, не обнаружить в них какой – либо период. В XVII веке в период зарождения современной науки разрабатываются методы изучения непрерывных процессов и приближённых вычислений. Отчетливое определение действительного числа даётся Ньютоном: «Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой – нибудь величины к другой величине того же рода, принятой нами за единицу». Введение новых чисел оказалось сильнейшее влияние на последующее развитие математики. Эта формулировка определяет действительное, рациональное и иррациональное число.
Заключительный этап в развитии понятия числа – введение комплексных чисел. Источником возникновения понятия комплексного числа явилось развитие алгебры. По – видимому, впервые идея комплексного числа возникла у итальянских математиков XVI века в связи с открытием алгебраического решения уравнений третьей и четвёртой степеней. Известно, что уже решение квадратного уравнения иногда приводит к действию извлечения квадратного корня из отрицательного числа. Практически задача, приводящаяся к решению такого квадратного уравнения, оказывается не имеющей решения. С открытием алгебраического решения уравнений третьей степени обнаружилась следующее обстоятельство. Как раз в том случае, когда все три корня уравнения являются действительными числами. По ходу вычисления, оказывается, необходимо выполнить действие извлечения квадратного корня из отрицательного числа. Возникающая при этом «мнимость» исчезает только по выполнении всех последующих действий. Это обстоятельство явилось первым стимулом к рассмотрению комплексных чисел, однако комплексные числа и действия над ними с трудом прививались в деятельности математиков. Остатки недоверия отражаются в сохранившемся до наших дней термине «мнимое» число. Это недоверие рассеялось лишь после геометрического истолкования комплексных чисел в виде точек на плоскости и установления несомненной пользы от введения комплексных чисел в теории алгебраических уравнений. Особенно после знаменитых работ Карла Гаусса.
Производя арифметические операции с действительными числами, мы не сомневаемся, что в итоге тоже получится действительное число (исключение составляет деление на нуль). Переходя к комплексным числам нужно убедиться в том, что арифметические операции над ними поражают только комплексные числа. Это значит, что результат любой арифметической операции должен быть представлен в стандартной форме.
Действительные числа удобно представлять в виде точек на числовой оси, таким образом, между точками плоскости и комплексными числами существует взаимно однозначное соответствие.
Можно вычислить и доказать что длина вектора, соответствующего комплексному числу равна его модулю. И также модуль суммы комплексных чисел не превосходит суммы их модулей. Также комплексное число можно определять не только парой координат, но и по – другому: парой модуль – аргумент.
При умножении комплексных чисел их модули необходимо перемножить, а аргументы – сложить. Нетрудно доказать, что при делении необходимо произвести обратные операции: поделить модули и вычесть аргументы.
Таким образом, с расширением понятия числа, специфические потребности некоторых областей математики вызвали различные обобщения понятия числа в других направлениях.
Расширение понятия числа
I. Множество натуральных чисел – это множество чисел, которыми пользуются при счете предметов.
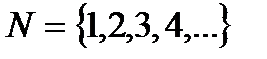 .
.
Всякому натуральному числу соответствует точка на числовой прямой.
Задание: Назовите самое маленькое натуральное число. Существует ли самое большое натуральное число?
II. Множество целых чисел – это множество, состоящее из натуральных чисел, им противоположных чисел и нуля.
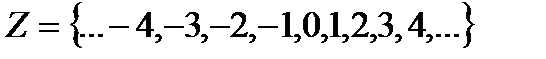 .
.
Всякому целому числу соответствует точка на числовой прямой.
Задания:
1. Существуют ли самое маленькое и самое большое целое число?
2. Верно ли утверждение:
a. любое натуральное число является целым;
b. любое целое число является натуральным?
III. Множество рациональных чисел – это множество несократимых дробей вида 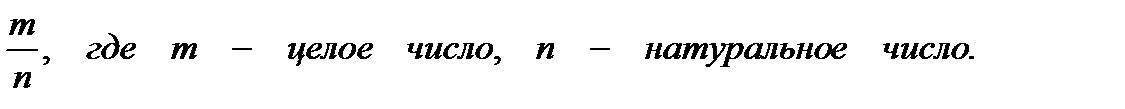
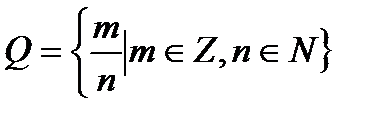 .
.
Всякому рациональному числу соответствует точка на числовой прямой.
Свойство рациональных чисел: Всякое рациональное число можно представить в виде бесконечной периодической десятичной дроби.
Обратно: всякая бесконечная периодическая десятичная дробь является рациональным числом.
Правило перевода периодических дробей в обыкновенные:
| Чисто периодические дроби | Смешанные периодические дроби |
Чистая периодическая дробь равна обыкновенной дроби, в числителе которой записан период, а в знаменателе – столько девяток, сколько цифр периоде.
Пример: 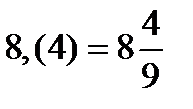 . .
| Смешанная периодическая дробь равна обыкновенной дроби, в числителе которой записана разность между числом до второго периода и числом до первого периода, а в знаменателе – число, составленное из стольких девяток, сколько цифр в периоде и стольких нулей, сколько цифр между запятой и периодом.
Пример: 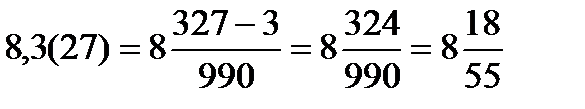 . .
|
Задания:
1. Докажите, что числа 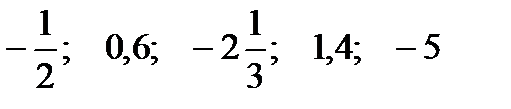 являются рациональными и отметьте эти числа на числовой прямой.
являются рациональными и отметьте эти числа на числовой прямой.
2. Верно ли утверждение:
а) всякое натуральное число является рациональным;
б) всякое целое число является рациональным;
в) верно ли утверждение: Всякое рациональное число является целым?
3. Представьте рациональные числа 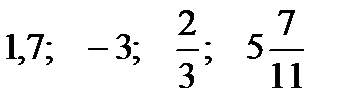 в виде бесконечных периодических десятичных дробей.
в виде бесконечных периодических десятичных дробей.
4. Переведите периодические дроби 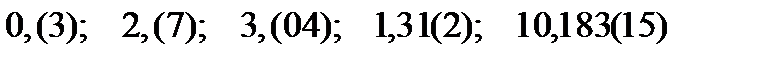 в обыкновенные. Проверьте результат перевода.
в обыкновенные. Проверьте результат перевода.
IV. Множество иррациональных чисел – это множество чисел, которые нельзя представить в виде несократимых дробей 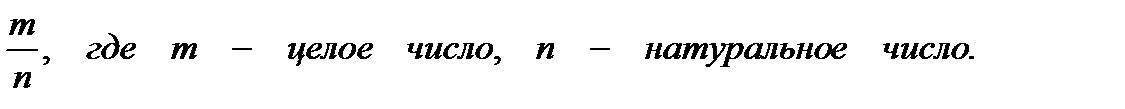
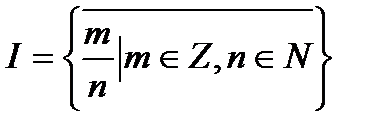 .
.
Всякому иррациональному числу соответствует точка на числовой прямой.
Свойство иррациональных чисел: Всякое иррациональное число представимо в виде бесконечной десятичной непериодической дроби.
Пример: π ≈ 3,1415926535897932384626433832795…;
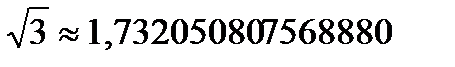 …
…
Задание: Докажите, что числа 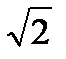 ,
, 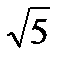 ,
, 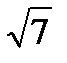 являются иррациональными.
являются иррациональными.
V. Множество действительных (вещественных) чисел – это объединение множеств рациональных и иррациональных чисел.
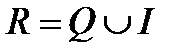 .
.
Каждому действительному числу соответствует точка на числовой прямой.
Обратно: каждой точке на числовой прямой соответствует определенное действительное число.
Следовательно, между множеством действительных чисел и множеством точек на числовой прямой существует взаимно-однозначное соответствие.
Задания:
1. Верно ли утверждение:
а) всякое целое число является действительным;
б) всякое рациональное число является вещественным;
в) всякое иррациональное число является вещественным;
г) всякое действительное число является рациональным;
д) всякое вещественное число является целым?
2. Даны числа: 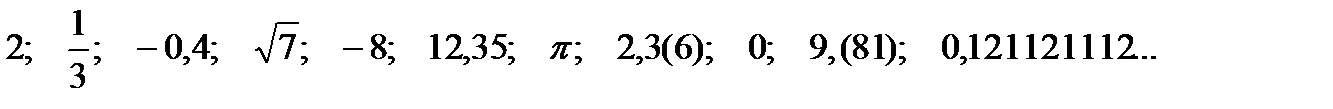 .
.
Выпишите: а) натуральные числа; б) целые числа; в) рациональные числа; г) иррациональные числа.
Модуль числа – это само число, если оно неотрицательно, и число, ему противоположное, если оно отрицательно.
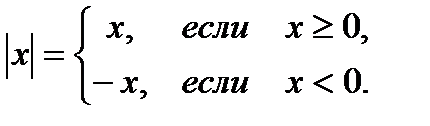
Примеры: 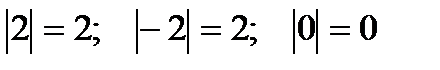 .
.
С геометрической точки зрения модуль числа – это расстояние от этого числа до начала отсчета.
Вывод: модуль числа отрицательным быть не может!
Задания:
1. Решите уравнения:
а) 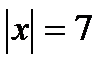 ;
б) ;
б) 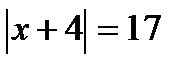 ;
в) ;
в) 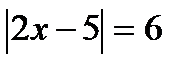 ;
г) ;
г) 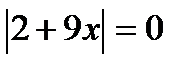 ;
д) ;
д) 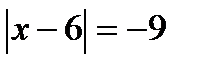 . .
| 2. Решите неравенства:
а) 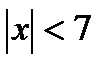 ;
б) ;
б) 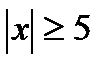 ;
в) ;
в) 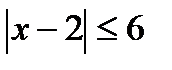 ;
г) ;
г) 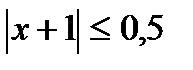 . .
| 3. Найдите расстояние между точками:
а) 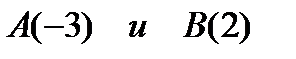 ;
б) ;
б) 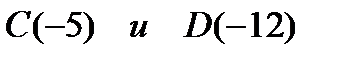 . .
|
Приближенные вычисления
Приближенное число есть такое число, которое отличается от точного на погрешность (ошибку), допущенную в соответствии с условиями данной задачи, и заменяет точное число в расчетной формуле.
Обозначим буквой a 0 точное число, а буквой a егоприближенное значение, тогда a 0 ≈ a.
Абсолютная погрешность приближенного значения числа – это модуль разности между точным и приближенным значением этого числа, т.е. 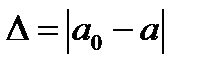 .
.
Так как точное число чаще всего неизвестно, то можно указать положительное число ∆ а, удовлетворяющее неравенству 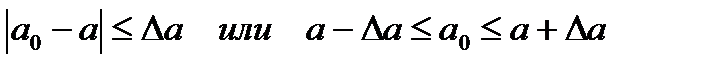 . Число ∆ а называется границей абсолютной погрешности.
. Число ∆ а называется границей абсолютной погрешности.
Задание:
1. Записать числа в виде двойного неравенства:
а) а = 347,50; ∆ а = 0,0047;
б) а 0 = 7,269 ± 0,0004.
2. Докажите, что число 1,7 является приближенным значением числа 1, 739 с точностью до 0,05.
3. Точное значение числа х неизвестно, а известно лишь, что
0,68 < х < 0,72. Найдите точность приближения h.
4. Вычислите приближенное значение величины х, равное среднему арифметическому границ, и укажите точность этого приближения, если: а) 3,6 ≤ х ≤ 4,2; б) 0,12 ≤ х ≤ 0,14.
Относительная погрешность приближенного значения числа – это отношение абсолютной погрешности этого числа к самому числу, т.е. 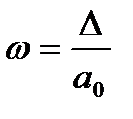 или в процентах
или в процентах 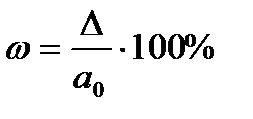 .
.
Так как в большинстве случаев истинное значение величины a 0 неизвестно, то на практике относительную погрешность 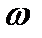 оценивают некоторым числом
оценивают некоторым числом 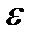 , большим этой погрешности.
, большим этой погрешности.
В качестве 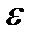 можно взять отношение
можно взять отношение 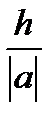 или любое число, большее этого отношения, но достаточно близкое к нему, т.е.
или любое число, большее этого отношения, но достаточно близкое к нему, т.е. 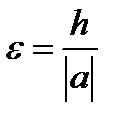 .
.
Число 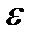 называется границей относительной погрешности.
называется границей относительной погрешности.
Качество измерений или вычислений тем лучше, чем меньше граница относительной погрешности.
Пример: Пусть а 0 = 42,1 ± 0,2. Вычислить в процентах границу относительной погрешности приближенного значения величины а.
Решение: Имеем а = 42,1; h = 0,2. Следовательно, 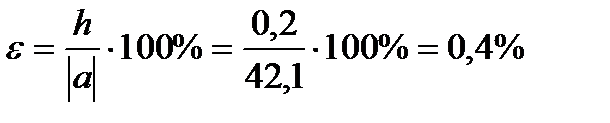 .
.
Задания:
1. Округлите число 123 до десятков и найдите абсолютную и относительную погрешность округления.
2. Округлите число 8, 2478 до сотых и найдите абсолютную и относительную погрешность округления.
3. Найдите относительную погрешность приближенных чисел:
а) 35,148 ± 0,00074;
б) 0,012 ± 0,001;
в) 17,2 ± 0,25.
4. Установите, какое равенство точнее: 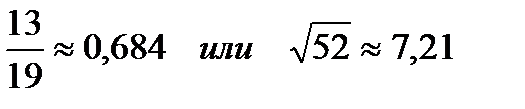 .
.
5. Найдите верхнюю и нижнюю границы, если приближенное значение числа и относительная погрешность в процентах соответственно равны:
а) 18 и 1%;
б) 0,6 и 15%.
Комплексные числа
Определение 1. Число, квадрат которого равен -1, называется мнимой единицей и обозначается буквой i. i 2 = -1.
Следовательно, 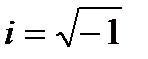 .
.
Определение 2. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, называются комплексными.
Данная форма записи комплексного числа называется алгебраической.
Число а является действительной частью комплексного числа, bi – его мнимой частью, число b называется коэффициентом при мнимой части.
Если b = 0, то комплексное число a + bi = a + 0i = a, то есть является действительным числом.
Вывод: действительные числа являются частным случаем комплексных чисел.
Если а = 0, то комплексное число a + bi = bi и называется чисто мнимым.
Сложение, вычитание и умножение комплексных чисел выполняется по правилам соответствующих действий над многочленами.
Задания:
1. Выполните сложение, вычитание и умножение комплексных чисел:
а) z 1 = 3+5 i и z 2 = 7–2 i;
б) z 1 = -2+3 i и z 2 = 7–4 i;
в) z 1 = 3–2 i и z 2 = 7– i;
г) z 1 = 1– i и z 2 = 1+ i;
д) z 1 = 3–9 i и z 2 = 5+2 i.
Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью (a + bi и a – bi).
Произведение двух сопряженных комплексных чисел всегда равно действительному числу (проверьте!).
Для деления одного комплексного числа на другое необходимо умножить делимое и делитель на комплексное число, сопряженное делителю.