Тест по теме: «Подобие треугольников» (8 класс)
1 вариант
1. Укажите условия, при которых 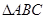 и
и  были бы подобны по третьему признаку.
были бы подобны по третьему признаку.
а)  ; в)
; в) 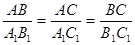 ;
;
б)  ; г)
; г) 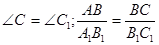 .
.
2. У треугольников АВС и DEF равны углы А и D. Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по первому признаку:
а) 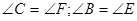 ; б)
; б) 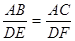 ; в)
; в)  ; г)
; г)  .
.
3. В треугольниках АВС и MNK 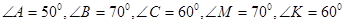 . Чему равен угол N?
. Чему равен угол N?
а)500; б)600; в)700.
4. Установите по рисунку, верно ли данное утверждение: 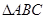 ~
~ 
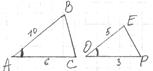
а)ДА; б)НЕТ; в)Не возможно установить.
5. 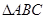 ~
~  , АВ=4, ВС=6, АС=7, А1В1=8. Сторона В1С1 равна:
, АВ=4, ВС=6, АС=7, А1В1=8. Сторона В1С1 равна:
а)3; б)12; в)14.
6. В треугольниках ABC и 
 .
.
Если ВС=10, то В1С1 равна:
а)25; б) 4; в) 5.
7. Соответствующие катеты двух подобных прямоугольных треугольников равны 5 дм и 10 дм. Найдите гипотенузу большего треугольника, если гипотенуза меньшего равна 7 дм.
а)14; б) 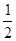 ; в) 2.
; в) 2.
Тест по теме: «Подобие треугольников» (8 класс)
2 вариант
1. Укажите условия, при которых 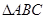 и
и  были бы подобны по первому признаку.
были бы подобны по первому признаку.
а)  ; в)
; в) 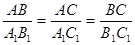 ;
;
б)  ; г)
; г) 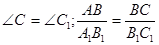 .
.
2. У треугольников АВС и DEF равны углы А и D. Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по второму признаку:
а) 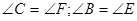 ; б)
; б) 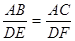 ; в)
; в)  ; г)
; г)  .
.
3. В треугольниках АВС и MNK  . Чему равен угол N?
. Чему равен угол N?
а)350; б)750; в)800.
4. Установите по рисунку, верно ли данное утверждение: 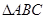 ~
~ 

а)ДА; б)НЕТ; в)Не возможно установить.
5. 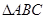 ~
~  , АВ=2, ВС=3, АС=1, А1В1=8. Сторона В1С1 равна:
, АВ=2, ВС=3, АС=1, А1В1=8. Сторона В1С1 равна:
а)12; б)4; в)6.
6. В треугольниках ABC и 
 .
.
Если ВС=12, то В1С1 равна:
а)6; б) 18; в) 3.
7. Соответствующие катеты двух подобных прямоугольных треугольников равны 6 м и 18 м. Найдите гипотенузу меньшего треугольника, если гипотенуза большего равна 27 дм.
а)  ; б) 3; в) 9.
; б) 3; в) 9.
Тест. Подобные треугольники
Заполните пропуски (многоточия), чтобы получилось верное высказывание.
ВАРИАНТ 1
1.Запись  означает, что отрезки АВ
и CD... отрезкам MN и FT.
2. На рисунке изображен параллелограмм ABCD, поэтому подобными являются треугольники... и.... означает, что отрезки АВ
и CD... отрезкам MN и FT.
2. На рисунке изображен параллелограмм ABCD, поэтому подобными являются треугольники... и....
 3. На рисунке АС || МК, поэтому треугольник МВК подобен треугольнику....
3. На рисунке АС || МК, поэтому треугольник МВК подобен треугольнику....
 4. Если угол В равен..., то изображенные на рисунке треугольники ABC и KNM подобны.
4. Если угол В равен..., то изображенные на рисунке треугольники ABC и KNM подобны.
 5. На рисунке МК || АС, АВ = 15 см, МВ = 5 см, АС = 30 см. Длина отрезка МК =....
5. На рисунке МК || АС, АВ = 15 см, МВ = 5 см, АС = 30 см. Длина отрезка МК =....
 6. На рисунке изображена трапеция ABCD, причем АО = 27 см, ВО = 18 см, ОС = 21 см. Длина отрезка OD равна....
6. На рисунке изображена трапеция ABCD, причем АО = 27 см, ВО = 18 см, ОС = 21 см. Длина отрезка OD равна....
 7. Площади двух подобных многоугольников равны 75 см2 и 300 см2. Одна из сторон второго многоугольника равна 9 см. Поэтому сходственная сторона первого многоугольника равна....
8. Сходственные стороны двух подобных треугольников равны 5 дм и 10 дм. Периметр первого треугольника равен 60дм, периметр второго треугольника равен....
9*. Известно, что ∆АВС - прямоугольный треугольник с прямым углом С, a CD - высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников... и... следует, что AC2 =AB*AD.
7. Площади двух подобных многоугольников равны 75 см2 и 300 см2. Одна из сторон второго многоугольника равна 9 см. Поэтому сходственная сторона первого многоугольника равна....
8. Сходственные стороны двух подобных треугольников равны 5 дм и 10 дм. Периметр первого треугольника равен 60дм, периметр второго треугольника равен....
9*. Известно, что ∆АВС - прямоугольный треугольник с прямым углом С, a CD - высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников... и... следует, что AC2 =AB*AD.
| Тест. Подобные треугольники
Заполните пропуски (многоточия), чтобы получилось верное высказывание.
ВАРИАНТ 2
1.Запись  означает, что отрезки CD
и MP... отрезкам AN и BK.
2. На рисунке изображен параллелограмм АВСD, поэтому подобными являются треугольники... и.... означает, что отрезки CD
и MP... отрезкам AN и BK.
2. На рисунке изображен параллелограмм АВСD, поэтому подобными являются треугольники... и....
 3. На рисунке АВ || KD, поэтому треугольник DKC подобен треугольнику....
3. На рисунке АВ || KD, поэтому треугольник DKC подобен треугольнику....
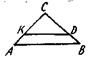 4. Если АС =..., KN =..., то изображенные на рисунке треугольники ABC и KNM подобны.
4. Если АС =..., KN =..., то изображенные на рисунке треугольники ABC и KNM подобны.
 5. На рисунке МК || АС, ВК = 20 см, МК = 10 см, ВС = 30см. Длина отрезка АС =....
5. На рисунке МК || АС, ВК = 20 см, МК = 10 см, ВС = 30см. Длина отрезка АС =....
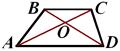
 6. На рисунке изображена трапеция ABCD, причем АО = 20 см, ОС = 3 см, AD = 30см. Длина отрезка ВС =....
6. На рисунке изображена трапеция ABCD, причем АО = 20 см, ОС = 3 см, AD = 30см. Длина отрезка ВС =....
 7. Сходственные стороны двух подобных многоугольников равны 20 см и 10 см. Площадь большего многоугольника равна 160 см2, площадь меньшего многоугольника равна....
8. Периметры подобных треугольников равны 75 см и 300 см. Одна из сторон большего треугольника равна 20 см, сходственная сторона меньшего треугольника равна....
9*. Известно, что ∆АВС - прямоугольный треугольник с прямым углом С, a CD - высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников... и... следует, что
ВС2 = AB*BD.
7. Сходственные стороны двух подобных многоугольников равны 20 см и 10 см. Площадь большего многоугольника равна 160 см2, площадь меньшего многоугольника равна....
8. Периметры подобных треугольников равны 75 см и 300 см. Одна из сторон большего треугольника равна 20 см, сходственная сторона меньшего треугольника равна....
9*. Известно, что ∆АВС - прямоугольный треугольник с прямым углом С, a CD - высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников... и... следует, что
ВС2 = AB*BD.
|