Предлагаемая стратегия бесцентрового измерения круглости деталей на основе адаптивной подналадки предполагает многократное измерение одной детали. Первое измерение позволяет выявить гармонический состав профиля в первом приближении. Эти данные используются для моделирования по разработанной модели, результатом работы которой будут новые параметры наладки прибора. После повторного измерения с принятой наладкой проводится сравнение полученных значений гармонического состава и круглости с первоначальными. Если величина круглости не уменьшается, то считается, что параметры наладки оптимальны. В противном случае процесс моделирования и подналадки повторяется. Как правило, на практике процесс подналадки ограничивается двумя или тремя измерениями.
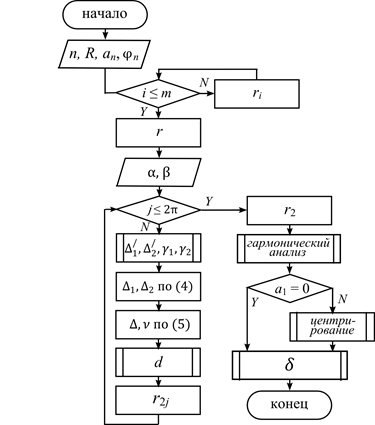
На основе математической модели бесцентрового измерения разработан алгоритм (рис. 3) и программа на языке С++. Алгоритм включает два цикла: задание профиля детали по углу j с переменной i от 1 до m (m – число точек на профиле); вращение детали при измерении по углу с переменной j от 0 до 2p. В ходе выполнения первого цикла формируется поперечный профиль детали в виде совокупности радиусов-векторов ri на основе исходных данных (n, an, j n) о гармоническом составе круглости. Во втором цикле проводится расчет погрешности базирования по формулам (2) – (6) и определяются измеренные радиусы r 2 профиля детали по выражению (7). Причем число исходно заданных точек профиля и число измеренных точек может не совпадать. По результатам моделирования возможно нахождение оптимальных параметров настройки прибора по углам a и b в интерактивном режиме. Процедуры гармонического анализа, центрирования круглограммы и расчета отклонения от круглости по различным методикам считаются известными и на схеме показаны условно.
Проведенные численные эксперименты показали, что при использовании одной призмы с постоянным углом и угловым положением датчика нельзя обеспечить не только приемлемую погрешность измерения для всех гармоник, но и примерно постоянную для первых 20-и гармоник. Этот результат соответствует аналогичным данным, приведенным в работе [6]. Систематическая погрешность составляет примерно от 5 % для 9 гармоники до 105 % для 8 гармоники. Полученные результаты могут быть использованы при настройке прибора только при наличии одной доминирующей гармоники в профиле детали, что редко встречается в технологии изготовления. Принцип суперпозиции при моделировании бесцентрового измерения не соблюдается в виду нелинейности системы, поэтому рекомендации для отдельных гармоник не позволяют эффективно минимизировать погрешность измерения в реальных производственных условиях.
Пример моделирования бесцентрового измерения реальной детали для двух вариантов настройки прибора показан на рис. 4. Синим цветом показан действительный профиль, красным – измеренный (отклонение от круглости 1,8 мкм, увеличение 1000, средний радиус записи 15 мм). Параметры наладки прибора рис. 4, а – a = 90°, b = 0; рис. 4, б – a = 60°, b = 45°. Погрешность измерения составила в первом варианте 42 %, а во втором 0,5 %. Видно, что в обоих случаях измеренный профиль отличается от действительного и дополнительно требуется центрирование круглограммы. Однако по результатам первого измерения удается определить примерный состав гармонических погрешностей профиля детали и на основании этого провести моделирование с нахождением наилучшего значения параметров настройки прибора для второго измерения.
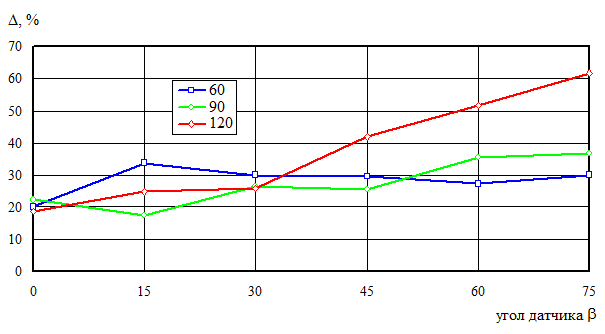
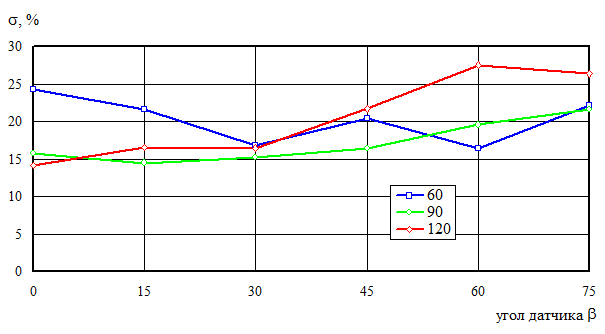
С целью исследования систематической погрешности и путей ее минимизации проведены измерение и моделирование для 50 наружных колец подшипников диаметром 30 мм с допуском круглости 0,002 мм. Эталонные измерения, по которым задавался действительный профиль деталей, выполнялись на прецизионном кругломере модели Talyrond 30. Варьировались угол призмы a = 60, 90, 120° и угол датчика b = 0, 15, 30, 45, 60, 75°. Результаты представлены на рис. 5 для среднего значения относительной погрешности и на рис. 6 – для стандартного отклонения погрешности измерения.
По графикам можно позволяет сделать вывод, что и угол призмы и угол датчика влияют на погрешность измерения. Для отдельных деталей и параметров настройки прибора относительная погрешность измерения достигала 120 %. Для партии деталей наихудшее значение относительной погрешности составляет 62 % и соответствует параметрам a = 120°, b = 75°, наилучшее равно 17,5 % для параметров a = 90°, b = 15°. Стандартное отклонение для указанных вариантов настройки составило 26 % и 14,5 % соответственно. Таким образом, оптимальная наладка для партии деталей позволяет одновременно уменьшить среднее значение систематической погрешности и ее размах. Минимальное значение стандартного отклонения не всегда соответствует минимальному среднему значению погрешности. Однако это важно только при оптимальной настройке прибора на конкретную партию деталей.
Рассмотренные измерения проводились для прецизионных деталей подшипников с малым значением круглости по сравнению с диаметром. Дополнительные измерения менее точных деталей с большим значением отклонения от круглости установили, что для них систематическая погрешность измерения незначительно возрастает. Однако общие закономерности по оптимальной настройке процесса измерения остаются справедливыми.
Для приведенных данных была проведена настройка прибора не только на партию деталей, но и на каждую деталь в отдельности в соответствии с обоснованной стратегией адаптивной подналадки. Оптимальная настройка обеспечила среднее значение погрешности 4,11 % и стандартное отклонение 4,12 % для 50 деталей. При этом выбор угла призмы также ограничивался только тремя значениями a = 60, 90, 120°. Очевидно, что более тонкая настройка прибора по углу призмы и углу датчика позволит еще эффективнее снижать систематическую погрешность измерения. Трудоемкость таких измерений возрастает, но моделирование по разработанной программе реализуется гораздо быстрее, чем собственно измерение на приборе. Поэтому по производительности бесцентровое измерение не будет уступать координатному или радиусному методам.
Выводы
Анализ показал, что измеренное значение круглости в подавляющем числе случаев превышает действительное значение. Поэтому при контроле возрастает вероятность совершить a-ошибку. В тоже время, если измеренное значение круглости укладывается в допуск, то можно гарантировать минимальную вероятность совершить b-ошибку. Это особенно актуально при контроле в условиях массового производства деталей, например, в автомобильной и подшипниковой промышленности.
Проведенные исследования позволяют сделать вывод о том, что бесцентровое измерение круглости на призме с датчиком малых линейных перемещений имеет систематическую погрешность, сложно зависящую от гармонического состава отклонений формы деталей. Принцип суперпозиции для совокупности гармоник не соблюдается в виду нелинейности системы.
Относительная погрешность измерений в экспериментах максимальная достигала 120 %. С другой стороны параметры настройки прибора – угол призмы и положение датчика – также влияют на систематическую погрешность. Оптимальная настройка прибора способствует снижению погрешности измерений до величины, не превышающей 5 %. Настройку прибора целесообразно выполнять на основе моделирования по предложенному алгоритму в несколько этапов. Оптимальные параметры настройки можно найти как для каждой детали, так и для некоторой партии деталей.
Заключение
Обоснованная стратегия бесцентрового измерения круглости на основе адаптивной подналадки с использованием новой математической модели позволяет эффективно минимизировать систематическую погрешность. В этом случае бесцентровое измерение становится хорошей альтернативой методам измерения на прецизионных кругломерах или координатно-измерительных машинах, более доступной для пользователей. Несколько уступая им по точности, бесцентровый метод имеет высокую производительность, малую стоимость и не требует высококвалифицированного обслуживающего персонала. Рекомендуется для контроля в массовом производстве деталей высокой и средней точности, как в лабораторных условиях, так и непосредственно в цехе на производстве.
Ссылки
[1] Авдулов А.Н. Контроль и оценка круглости деталей машин. М.: Изд-во стандартов, 1974. 176 с.
[2] Палей М.А., Чудов В.А. О возможностях седлообразных приборов при контроле диаметров и отклонений формы // Измерительная техника. 1972. № 4. С. 20-21.
[3] Прецизионный кругломер / Я. И. Биндер, И. Д. Гебель, А. И. Нефедов и др. // Измерительная техника. 1999. № 8. C. 25-27.
[4] Zakharov O.V., Brzhozovskii B.M. Accuracy of centering during measurement by roundness gauges // Measurement Techniques. 2006. Volume 49. Number 11. Pp. 1094-1097.
[5] Сысоев Ю.С. Координатные методы определения параметров средней окружности при анализе профиля реальной поверхности // Измерительная техника. 1995. № 10. С. 22-25.
[6] Witzke F. W. Measuring roundness in place // American Machinist. 1969, v. 113, № 1, pp. 103-106.
[7] Zakharov O.V., Pogorazdov V.V., Kochetkov A.V. Methodological Principles in the Harmonic Analysis of Cyclograms // Metrologiya. 2004. № 6. P. 3-10.
[8] Spragg R.C. Accurate Calibration of Surface Texture and Roundness Measuring Instruments // Proceedings of the Institution of Mechanical Engineers, Conference Proceedings. September 1967. vol. 182. № 11. pp. 397-405.
[9] Changcai Cui, Wei Fan, Fugui Huang. An iterative neighborhood search approach for minimum zone circularity evaluation from coordinate measuring machine data // Measurement Science and Technology. 2010. Volume 21. Number 2. p. 027001.
[10] Xiuming Li, Hongqi Liu. A simple and efficient algorithm for evaluation of roundness error // Measurement Science and Technology. 2012. Volume 23. Number 8. p. 087003.
Перечень подрисуночных подписей
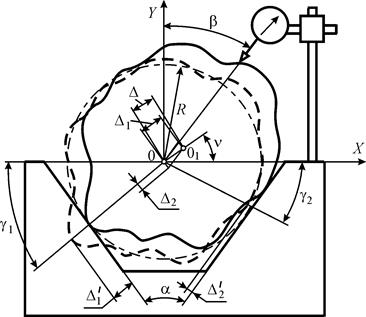
Рис. 1. Расчетная схема измерения
Рис. 2. Алгоритм расчета
Рис. 3. Моделирование измерения
Рис. 4. Относительная погрешность измерения, среднее значение
Рис. 5. Относительная погрешность измерения, стандартное отклонение
Гармонический анализ
Центрирование
Угол датчика
Фигура 1
Фигура 2
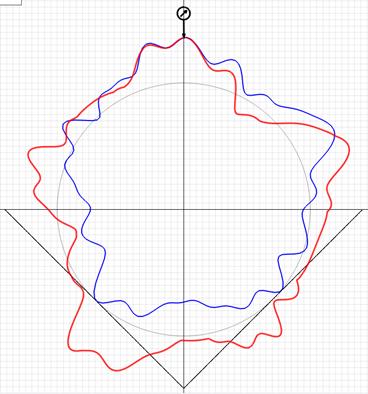
а

б
Фигура 3
Фигура 4
Фигура 5