Критерии оценивания:
- для получения оценки «3» необходимо выполнить 4 задания 1 части;
- для получения оценки «4» необходимо выполнить все задания 1 части и 1 задание из 2 части;
- для получения оценки «5» необходимо выполнить все задания 1 части и 2 или 3 задания из 2 части.
1 вариант
1 часть
1. Площадь прямоугольного треугольника равна  . Один из острых углов равен 300. Найдите длину катета, прилежащего к этому углу.
. Один из острых углов равен 300. Найдите длину катета, прилежащего к этому углу.
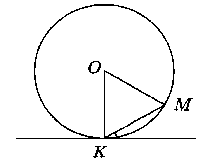
2. Прямая касается окружности в точке К. Точка О – центр окружности. Хорда КМ образует с касательной угол, равный 40. Найдите величину угла ОМК. Ответ дайте в градусах.
3. Найдите площадь параллелограмма, изображенного на рисунке

4. На клетчатой бумаге изображен угол. Найдите его градусную величину.

5. Какое из следующих утверждений верно?
1. Все углы ромба равны.
2. Если стороны одного четырехугольника соответственно равны сторонам другого четырехугольника, то такие четырехугольники равны.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Часть 2
6. Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF=21, BF=20.
7. Сторона ВС параллелограмма ABCD вдвое больше стороны АВ. Точка Е – середина стороны ВС. Докажите, что АЕ – биссектриса угла BAD.
8. Углы при одном из оснований трапеции равны 190 и 710, а отрезки соединяющие середины противоположных сторон, равны 12 и 10. Найдите основания трапеции.
2 вариант
1часть
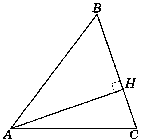
1. В остроугольном треугольнике АВС высота AH равна  , а сторона АВ равна 60. Найдите cos B.
, а сторона АВ равна 60. Найдите cos B.
2. Касательные в точках А и В к окружности с центром О пересекаются под углом 560. Найдите угол АВО. Ответ дайте в градусах.

3. В параллелограмме ABCD диагональ АС в 2 раза больше стороны АВ и ∟ACD=740. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

4. На клетчатой бумаге изображен угол. Найдите его градусную величину.

5.Какие из следующих утверждений верны:
1. Через любую точку проходит не менее одной прямой.
2. Сумма смежных углов равна 900.
3. Если при пересечении двух прямых третьей прямой соответственные углы равны 650, то эти две прямые параллельны.
2 часть
6. На стороне CD параллелограмма ABCD отметили точку М. Найдите площадь параллелограмма, если площадь треугольника МАВ равна 19.
7. Внутри параллелограмма ABCD выбрали произвольную точку Е. докажите, что сумма площадей треугольников ВЕС и АЕD равна половине площади параллелограмма.
8. Углы при одном из оснований трапеции равны 370 и 530, а отрезки, соединяющие середины противоположных сторон, равны 21 и 12. Найдите основания трапеции.
3 вариант
1 часть
1. В треугольнике АВС АС=ВС. Внешний угол при вершине В равен 1400. Найдите угол С. Ответ дайте в градусах. 
2. Четырехугольник ABCD вписан в окружность. Угол АВС равен 1120, угол САDравен 700. Найдите угол АВD. Ответ дайте в градусах.

3. Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
4. Площадь параллелограмма ABCD равна 5. Точка Е – середина стороны АD. Найдите площадь трапеции АЕСВ. 
5. Какие из следующих утверждений верны?
1. Если угол равен 600, то смежный с ним равен 1200.
2. Через любую точку проходит ровно одна прямая.
3. Если при пересечении двух прямых третьей прямой сумма внутренних накрест лежащих углов равна 1800, то эти две прямые параллельны.
2 часть
6. Окружность, вписанная в треугольник АВС, касается его сторон в точках М, К и Р. Найдите углы треугольника АВС, если углы треугольника МКР равны 520, 560 и 720.
7. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВС и AD в точках L и G соответственно. Докажите, чтоCL=AG.
8. В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК:КМ=10:9. Прямая АК пресекает сторону ВС в точке Р. Найдите отношение площади четырехугольника КРСМ к площади треугольника АВС.
4 вариант
1 часть
1. В треугольнике АВС стороны АС и ВС равны 5, АВ=  . Найдите sin A.
. Найдите sin A.
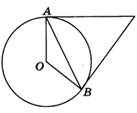
2. Касательные в точках А и В к окружности с центром О пересекаются под углом 680. Найдите угол АВО. Ответ дайте в градусах.
3. Периметр ромба равен 80, а один из углов равен 300. Найдите площадь ромба.
4. На клетчатой бумаге с размером клетки 1см х 1см отмечены точки А, В и С.найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

5.Какое из следующих утверждений верно?
1. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2. Сумма углов равнобедренного треугольника равна 180 градусов.
3. Диагонали ромба равны.
2 часть
6. Точка Н является основанием высоты ВН, проведенной из вершины прямого угла В прямоугольного треугольника АВС. Окружность с диаметром ВН пересекает стороны АВ и CD в точках Р и К соответственно. Найдите ВН, если РК=15.
7. В выпуклом четырехугольнике ABCD углы ABD и АВС равны. Докажите, что углы DAC и DBC также равны.
8. Углы при одном из оснований трапеции равны 390 и 510, а отрезки, соединяющие середины противоположных сторон трапеции, равны19 и 3. Найдите основания трапеции.
5 вариант
1 часть
1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
2. В окружности с центром О АС и BD – диаметры. Центральный угол AOD равен 860. Найдите вписанный угол АСВ. Ответ дайте в градусах.

3. Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
4. Из квадрата вырезали прямоугольник (см. рис). Найдите площадь получившейся фигуры.

5.Какие из следующих утверждений верны?
1. Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
2. все диаметры окружности равны между собой.
3. Один из углов треугольника всегда не превышает 600.
2 часть
6. На стороне AD параллелограмма ABCD отметили точку М. Найдите площадь параллелограмма, если площадь треугольника МВС равна 7.
7. Докажите, что окружность, построенная на стороне остроугольного треугольника как на диаметре, пересекает две другие стороны в основаниях высот.
8. Окружности радиусов 45 и 55 касаются внешним образом. Точки А и В лежат на первой окружности, точки C и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АB и СD.
6 вариант
1 часть
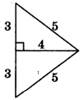
1. Найдите площадь треугольника, изображенного на рисунке.
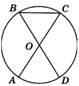
2. В окружности с центром О АС и ВD – диаметры. Центральный угол AOD равен 380. Найдите вписанный угол АСВ. Ответ дайте в градусах.
3. В трапеции ABCD AD=6, ВС=3, а ее площадь равна 27. Найдите площадь треугольника АВС.

4. Площадь одной клетки равна 1. Найдите площадь фигуры, изображенной на рисунке.

5.Какое из следующих утверждений верно?
1. Диагонали ромба равны.
2. Отношение площадей подобных треугольников равно коэффициенту подобия.
3. В треугольнике против большей стороны лежит больший угол.
2 часть
6. Около трапеции, один из углов которой равен 360, описана окружность. Найдите остальные углы трапеции.
7. В трапеции ABCD с основаниями АD и ВС диагонали пересекаются в точке О. докажите, что площади треугольников АОВ и СОD равны.
8. Две касающиеся внешним образом в точке К окружности, радиусы которых равны 6 и 24, касаются сторон угла с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С. Найдите радиус окружности, описанной около треугольника АВС.
7 вариант
1 часть
1. В треугольнике АВС угол С прямой, ВС=2, sin A =0,4. Найдите АВ.
2. Четырехугольник ABCD вписан в окружность. Угол АBD равен 850, угол CAD равен 190. Найдите угол АВС. Ответ дайте в градусах.

3. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 34, отсекает треугольник, периметр которого равен 69. Найдите периметр трапеции.
4. На клетчатой бумаге изображен угол. Найдите его градусную величину.

5.Какое из следующих утверждений верно?
1. Диагонали ромба точкой пересечения делятся пополам.
2. В тупоугольном треугольнике все углы тупые.
3. Каждая из биссектрис равнобедренного треугольника является его высотой.
2 часть
6. Высота АН ромба ABCD делит сторону CD на отрезки DH=8 и СН=2. Найдите высоту ромба.
7. В треугольнике АВС проведены высоты АК и BL. Докажите, что около четырехугольника ALKB можно описать окружность.
8. Углы при одном из оснований трапеции равны 230 и 670, а отрезки, соединяющие середины противоположных сторон, равны 15 и 8. Найдите основания трапеции.
8 вариант
1 часть
1. в треугольнике АВС стороны АС и ВC равны, АН – высота, cos ∟BAC =  . Найдите cos ∟BAН.
. Найдите cos ∟BAН.

2. окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и угол Авс равен 1240. Найдите величину угла ВОС. Ответ дайте в градусах.

3. Средняя линия трапеции равна 41, а меньшее основание равно 20. Найдите большее основание трапеции.
4. На клетчатой бумаге изображен угол. Найдите его градусную величину.

5.Какое из следующих утверждений верно?
1. Все углы ромба равны.
2. Любой прямоугольник можно вписать в окружность.
3. Диагональ трапеции делит ее на два равных треугольника.
2 часть
6. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках К и М соответственно. Найдите АС, если ВК:КА=3:4, КМ=18.
7. Сторона АВ параллелограмма ABCD вдвое больше стороны ВС. Точка N – середина стороны АВ. Докажите, что CN – биссектриса угла BCD.
8. Углы при одном из оснований трапеции равны 440 и 460, а отрезки, соединяющие середины противоположных сторон, равны 14 и 6. Найдите основания трапеции.