Теорема о вронскиане системы линейно независимых частных решений ЛОДУ
Пусть 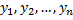 – линейно независимые на
– линейно независимые на 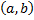 – частные решения ЛОДУ n-го порядка
– частные решения ЛОДУ n-го порядка 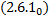 . Тогда
. Тогда 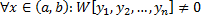
Док-во: (от противного)
Пусть 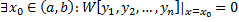 . Рассмотрим СЛАУ относительно
. Рассмотрим СЛАУ относительно  :
:
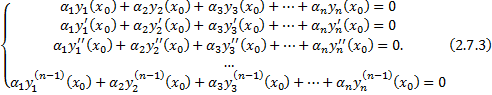
Ее определитель 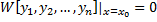 , следовательно, система имеет ненулевое решение, т.е.
, следовательно, система имеет ненулевое решение, т.е. 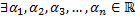 , не все равные
, не все равные 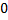 , такие, что выполняется система (2.7.3).
, такие, что выполняется система (2.7.3).
Рассмотрим частное решение ЛОДУ 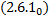 .
.
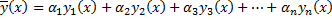 .
.
Оно удовлетворяет в т. 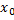 начальным условиям (в силу (2.7.3)):
начальным условиям (в силу (2.7.3)):
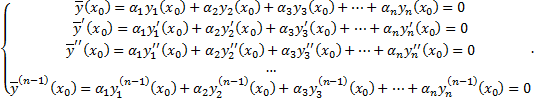
Рассмотрим частное решение ЛОДУ 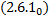
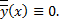
Оно удовлетворяет в т. 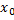 начальным условиям
начальным условиям
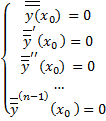 .
.
Таким образом, частные решения ЛОДУ 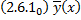 и
и 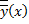 удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши
удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши 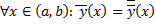 , т.е.
, т.е. 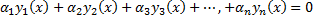 , т.е.
, т.е. 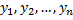 – линейно зависимы на
– линейно зависимы на 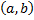 – противоречит условию линейной независимости
– противоречит условию линейной независимости 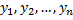 .
.
Т.е. 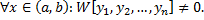
Замечание. Пусть 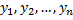 – частные решения ЛОДУ
– частные решения ЛОДУ 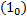 . График функции
. График функции 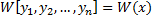 может иметь вид (см. рис. 37, 38):
может иметь вид (см. рис. 37, 38):
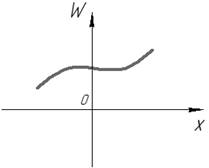 Рис. 37
Рис. 37
| 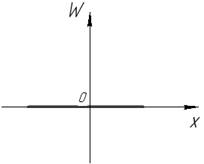 Рис. 38
Рис. 38
|
| (для линейно независимых решений) | (для линейно зависимых решений) |
Не может иметь вид (см. рис. 39, 40):
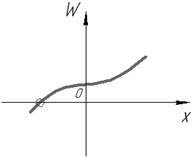 Рис. 39
Рис. 39
| 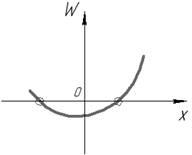 Рис. 40
Рис. 40
|
Теорема о размерности пространства решений ЛОДУ n-го порядка. Фундаментальная система решений. Структура общего решения.
Теорема о размерности пространства решений ЛОДУ n-го порядка
Размерность пространства решений ЛОДУ n-го порядка равна n.
Док-во: нужно доказать, что существует базис пространства решений, состоящий из 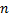 частных решений, т.е.
частных решений, т.е. 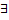 частные решения
частные решения 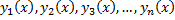 , которые удовлетворяют следующим условиям:
, которые удовлетворяют следующим условиям:
1. Они линейно независимы на 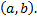
2. Любое частное решение 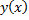 имеет вид
имеет вид 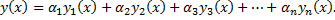
1. рассмотрим частные решения ЛОДУ 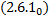
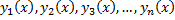 , удовлетворяющие начальным условиям:
, удовлетворяющие начальным условиям:

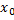 – фиксированная точка интервала
– фиксированная точка интервала 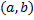 .
.
По теореме существования и единственности решения задачи Коши 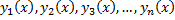 определены на всем интервале
определены на всем интервале 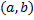 .
.
Т.к.  , то функции
, то функции 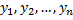 – линейно независимы на
– линейно независимы на 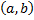 , т.к. иначе
, т.к. иначе 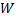 должен был бы равняться нулю.
должен был бы равняться нулю.
2. Рассмотрим произвольное частное решение 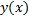 .
.
Оно удовлетворяет некоторым начальным условиям:
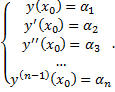
Рассмотрим частное решение 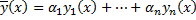 . Оно удовлетворяет начальным условиям:
. Оно удовлетворяет начальным условиям:
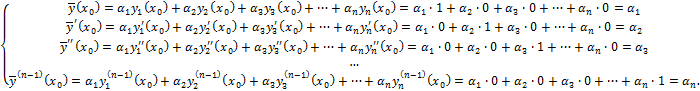
Т.е. 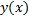 и
и 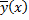 удовлетворяют одинаковым начальным условиям в точке
удовлетворяют одинаковым начальным условиям в точке 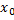 . По теореме о единственности решения
. По теореме о единственности решения 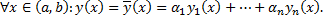
Опр. Система n линейно независимых частных решений ЛОДУ n -го порядка 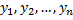 называется фундаментальной системой решений (ФСР) ЛОДУ.
называется фундаментальной системой решений (ФСР) ЛОДУ.
ФСР – базис линейного пространства решений.
Теорема о структуре общего решения ЛОДУ n-го порядка
Пусть 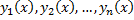 – ФСР. Тогда общее решение имеет вид:
– ФСР. Тогда общее решение имеет вид:
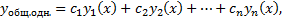
 – произвольные постоянные.
– произвольные постоянные.
Док-во: нужно доказать, что для 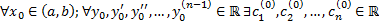 такие, что частное решение
такие, что частное решение 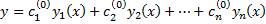 удовлетворяет начальным условиям:
удовлетворяет начальным условиям:
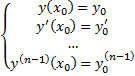 .
.
Решение 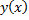 , удовлетворяющее данным начальным условиям, существует и определено на всем
, удовлетворяющее данным начальным условиям, существует и определено на всем 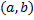 .
. 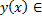 линейному пространству решений и разлагается по базису
линейному пространству решений и разлагается по базису 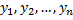 линейного пространства:
линейного пространства:
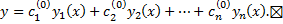
2.9. ЛОДУ с постоянным коэффициентами. Характеристическое уравнение и построение общего решения по его корням (вывод для 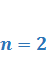 ).
).
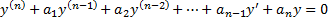 ,
,
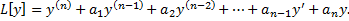
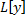 – линейный дифференциальный оператор с постоянными коэффициентами:
– линейный дифференциальный оператор с постоянными коэффициентами:
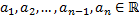 .
.
Рассмотрим случай 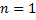 :
:
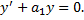
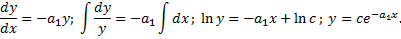
Для произвольного 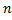 найдем частное решение вида
найдем частное решение вида
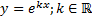 .
.
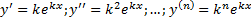 .
.
Тогда
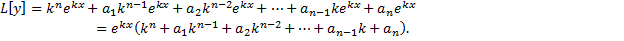
Опр. Уравнение 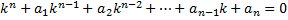 называется характеристическим уравнением ЛОДУ с постоянными коэффициентами.
называется характеристическим уравнением ЛОДУ с постоянными коэффициентами.
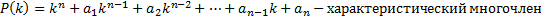
Таким образом, при 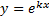 имеем
имеем 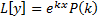 и функция
и функция 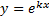 является частным решением
является частным решением 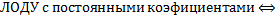
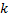 является корнем его характеристического уравнения.
является корнем его характеристического уравнения.