Пример 1. При 25 °С давление насыщенного пара воды составляет 3,166 кПа (23,75 мм. рт.ст.). Определите при той же температуре давление насыщенного пара над 5 % водным раствором карбамида CO(NH2)2.
Решение.
Для идеальных растворов при постоянной температуре в состоянии равновесия между раствором и газовой фазой над ним давление насыщенного пара каждого компонент рi выражается уравнением:
pi = 
,
где Ni – мольная доля компонента, 
– давление пара чистого компонента.
Вычислим мольную долю растворителя Ni по формуле:
,
где – n1 и n2 – число молей растворителя и растворенного вещества соответственно.
В 100 г раствора содержится 5 г карбамида (мольная масса 60 г/моль) и 95 г воды (мольная масса 18 г/моль). Количество карбамида и воды соответственно равно:
n2 = 
= 0,083 моль; n2 = 
= 5,278 моль.
Находим мольную долю растворителя (воды):
.
Следовательно:
pi = = 0,985×3,166 = 3,119 кПа (или 23,31 мм.рт.ст.).
Пример 2. Рассчитайте, при какой температуре должен кристаллизоваться раствор, содержащий в 250 г воды 54 г глюкозы C6H12O6.
Решение.
Понижение температуры замерзания растворителя (воды) выражается уравнением:
∆Ткрист = Ккр× сm,
где Ккр – криоскопическая постоянная данного растворителя, сm – моляльность раствора.
Определим моляльность раствора (М(С6Н12О6) = 180 г/моль)
моль/кг.
∆Ткрист = Ккр× сm = 1,86×1,2 = 2,23 °С.
Следовательно, раствор будет кристаллизоваться при –2,23 °С.
Пример 3. Раствор, содержащий 8 г некоторого вещества в 100 г диэтилового эфира, кипит при 36,86 °С, тогда как чистый эфир кипит при 35,60 °С. Определите молекулярную массу растворенного вещества.
Решение. Из условия задачи находим разность температур кипения:
∆Ткип = 36,86 – 35,60 = 1,26°
Повышение температуры кипения раствора определяется по уравнению:
∆Ткип = Кэб× сm,
где Кэб – эбуллиоскопическая постоянная растворителя.
Определяем моляльность раствора:
моль/1000 г эфира.
Молекулярную массу растворенного вещества найдем из соотношения
откуда 
г/моль.
Пример 4. Навеска вещества массой 12,42 г растворена в 500 см3 воды. Давление пара полученного раствора при 20 °С равно 3732,7 Па. Давление пара воды при той же температуре равно 3742 Па. Рассчитайте мольную массу растворенного вещества.
Решение. Пользуясь законом Рауля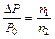 
и учитывая условия задачи, получим:
∆P = 3742 – 3732,7 = 9,3 Па; n2 =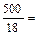 
27,78 моль,
тогда число молей (n1) растворенного вещества будет равно:
0,069 моль.
Поскольку 
, то M(в-ва) =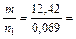 
180 г/моль.
Пример 5. Раствор, содержащий 0,85 г хлорида цинка в 125 г воды, кристаллизуется при –0,23 °С. Определите кажущуюся степень диссоциации ZnCl2.
Решени е. Найдем моляльную концентрацию сm соли в растворе. Поскольку мольная масса ZnCl2 равна 136,3 г/моль, то
моль/кг.
Определим понижение температуры кристаллизации без учета диссоциации электролита (Ккр воды равна 1,86):
∆Ткрист.выч. = Kкр× сm = 1,86×0,050 = 0,093 °С.
Сравнивая найденное значение с экспериментально определенным понижением температуры кристаллизации, вычисляем изотонический коэффициент i:
i = ∆Ткрист./∆Ткрист.выч. = 0,23/0,093 = 2,47.
Кажущуюся степень диссоциации a соли найдем из соотношения:
где n – общее число ионов (ZnCl2 ® Zn2+ + 2 Cl–)
Пример 6. При растворении гидроксида натрия массой 12 г в воде массой 100 г температура кипения повысилась на 2,65°. Определите степень диссоциации (%) гидрокcида натрия.
Решение. Для сильных электролитов имеем:
∆Ткип. = i×Кэб× сm.
Откуда
Тогда 
.
Пример 7. Определите осмотическое давление раствора сахарозы при 0°С, если при 20°С осмотическое давление этого же раствора равно 1,066×105 Па.
Решение. Осмотическое давление – это минимальное давление, которое нужно приложить к раствору, чтобы остановить осмос. Согласно закону Вант-Гоффа, осмотическое давление (кПа) равно:
,
где с – молярная концентрация раствора, моль/л; R – молярная газовая постоянная 8,314 
, Т – температура, К.
Определим концентрацию раствора сахарозы при известной температуре и осмотическом давлении
моль/л,
тогда осмотическое давление сахарозы при 0 °С составит:
= 0,044×8,314×273=99,7 кПа
Эбуллиоскопическая и криоскопическая константы, зависят только от природы растворителя.
Пример 6. относительное понижение упругости пара над раствором тростникового сахара (С12Н22О11) в воде составляет 2 %. Определите осмотическое давление этого раствора при температуре 47 ºС. Плотность раствора 1,15 г/см3. Определите изменение температуры плавления и кристаллизации, если K эб = 0,52 K·кг/моль, K кр = = 1,86 K·кг/моль,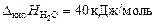 
; 
; 
.
Решение. Согласно закона Рауля мольная доля сахара в растворе составляет 0,02 (2%). Определим повышение температуры кипения раствора:
.
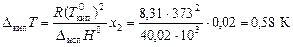Тогда понижение температуры замерзания раствора составит:
.
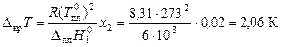вычислим осмотическое давление по формуле:
.
Пример 7. Раствор магния в олове содержит 0,833 г магния в 100 г олова. Температура плавления олова 505 К, а теплота плавления 7200 Дж/моль. Определить температуру начала кристаллизации этого раствора.
Решение. определим мольную долю х 2 магния в олове:
.
Вычислим температуру кристаллизации расплава:
Пример 8. В системе свинец (II)-серебро (I) при Т = 1490 К закон Рауля справедлив для растворов, содержащих менее 18 % свинца. Давление насыщенного пара над чистым серебром 7,47 Па. Вычислить давление пара серебра над раствором, содержащим 17,5 % свинца.
Решение. выделим мысленно 100 г расплава и примем их за 100 %, тогда 
. мольная доля свинца в сплаве
.
Вычислим давление пара серебра над расплавом
.
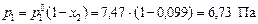Пример 9. Давление насыщенного пара над раствором, содержащим 5 г едкого натра в 180 г воды, при 100 ºС составляет 0,99·105 Па. Давление насыщенного пара над чистой водой при 100 ºС составляет 1,01·105 Па. Определите состояние едкого натра в растворе.
Решение. Состояние едкого натра в растворе можно оценить по величине изотонического коэффициента i. По закону Рауля
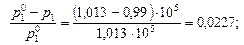
Вычислим изотонический коэффициент:
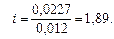
полученное значение i > 1 указывает на наличие диссоциации NaOH. Кажущаяся степень диссоциации
