Билет 7.
1. Вопрос
Генеральной совокупностью называется вся подлежащая изучению совокупность объектов.
Выборочной совокупностью (или выборкой) называется та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности объектов.
Числа объектов (наблюдений) в генеральной или выборочной совокупности называются их объемами.
Выборка должна быть отобрана случайно. Случайность достигается соблюдением принципа равной возможности всем элементам генеральной совокупности быть отобранными в выборку (жеребьевка; использование случайных чисел).
Виды выборок:
- собственно-случайная выборка (образовывается случайным выбором элементов без расчленения на части и группы);
- механическая выборка;
- стратифицированная выборка;
- серийная выборка.
Два способа образования выборок:
- повторный отбор (случайно отобранный и обследованный элемент возвращается в общую совокупность и может быть повторно отобран);
- бесповторный отбор (отобранный элемент не возвращается в общую совокупность).
Выборка называется репрезентативной, если она достаточно хорошо воспроизводит генеральную совокупность.
Сущность выборочного метода состоит в том, чтобы по некоторой выборке судить о генеральной совокупности в целом (преимущества и недостатки выборочного метода).
Основной задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки.
В дальнейшем используем обозначения:
xi – значения признака;
N и n – объемы генеральной и выборочной совокупностей;
Ni и ni – число элементов генеральной и выборочной совокупностей со значением признака xi;
M и m – число элементов генеральной и выборочной совокупностей, обладающих данным признаком.
Выборочный метод широко применяется на практике. Однако значение этой темы значительно шире, поскольку концепция выборки лежит в основе методологии математической статистики. Соотношение между характеристиками выборочной и генеральной совокупностей есть соотношение между опытными данными (результатами наблюдений) и теоретической моделью.
Чтобы по данным выборки можно было судить о генеральной совокупности, она должна быть отобрана случайно. Поэтому выборочные характеристики – выборочные средняя 
, доля w и дисперсия s 2 – величины случайные в отличие от их аналогов в генеральной совокупности 
, Р и s2 – величин неслучайных.
Необходимо знать свойства выборочных оценок: несмещенность, состоятельность, эффективность, уметь обосновать несмещенность и состоятельность выборочных средней и доли. При этом следует помнить, что основное требование, предъявляемое к выборочной оценке, заключается в том, чтобы ее рассеяние относительно оцениваемого параметра было минимальным. Для несмещенной оценки это требование означает ее эффективность. Но даже «наилучшая» оценка является лишь приближенным значением неизвестного параметра и, будучи величиной случайной, может существенно отличаться от самого параметра.
Вопрос
Полный факторный эксперимент требует избыточного числа опытов, если объект может быть описан линейной моделью. Следовательно, такой эксперимент характеризуется избыточным числом степеней свободы, которое может быть определено, как число опытов минус число коэффициентов линейной модели l = N- (к + 1). Для полного двухфакторного эксперимента число опытов N=4, к=2, следовательно, имеем одну степень свободы. Поскольку почти всегда имеется возможность сузить область эксперимента, то имеется возможность использовать линейную модель. Избыточную степень свободы возможно употребить для минимизации числа опытов. Для этого вектор-столбцу взаимодействия, которым можно пренебречь, присваивается имя нового фактора х1х2 = х3. Таким образом, план полного двухфакторного эксперимента используется для проведения дробного трехфакторного эксперимента. В итоге становится возможным в два раза сократить число опытов по сравнению с полным трехфакторным экспериментом. Матрица планирования будет иметь вид
| № | х1 | х2 | х1х2 = х3 |
| + | + | + | |
| + | - | - | |
| - | - | + | |
| - | + | - |
В рассмотренном выше случае была проведена замена х1х2 = х3 (а). Вместе с тем существует возможность замены -х1х2 = х3 (б). Если объединить два таких плана, то получится полный трехфакторный эксперимент.
Каждый из этих двух планов называется дробной репликой от полного факторного эксперимента (в рассмотренном случае - полурепликой). Если перемножить каждое из соотношений (а) и (б) на х3, то получим х1х2х3=1 или х1х2х3=-1. Произведение вектор-столбцов, численно равное ±1, называется определяющим контрастом. Он служит для того, чтобы определить, с каким фактором или взаимодействием смешан данный фактор или взаимодействие. Для этого определяющий контраст умножается на данный фактор (взаимодействие). После умножения определяющего контраста на этот фактор (взаимодействие), получают генерирующее соотношение, которое и определяет искомое взаимодействие, например, х1х2х3=1 умножаем на х2, получим х1х3 = х2.
Как полный, так и дробный многофакторный эксперименты не позволяют оценить коэффициент при квадратах соответствующих факторов, так как вектор-столбец 
равен вектор-столбцу х0.
Если в дробном факторном эксперименте р взаимодействий смешаны с k факторами, то такая дробная реплика обозначается как 2к-р. Если фактор связан с взаимодействием наивысшего порядка, то такая дробная реплика называется главной. В случае использования матрицы полного двухфакторного эксперимента для дробной реплики трехфакторного эксперимента есть только одна возможность смешать взаимодействие первого порядка (x1x2) с фактором х3 (х1х2 = х3). В таком случае получают дробную реплику разрешающей способности III: 
, которая определяется по числу факторов в определяющем контрасте (например, в случае х1х2х3 =1, разрешающая способность III).
Дробные реплики типа 2k-p позволяют сократить число опытов в 2p раз по сравнению с полным факторным экспериментом. Такие дробные реплики называют регулярными. Они полностью сохраняют свойства полного многофакторного эксперимента.
Билет 20.
Вопрос
Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной.
Критерии близости функций могут быть различные.
В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.
В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.
Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.
Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.
В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом.
В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная.
В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.
Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).
Аппроксимация линейной функцией
Любая линейная функция может быть записана уравнением
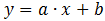
Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.
С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:
Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.
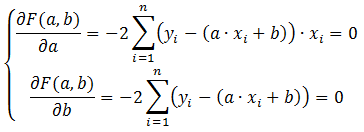
Решаем полученную систему уравнений
Определяем значения коэффициентов
Для вычисления коэффициентов необходимо найти следующие составляющие:
Тогда значения коэффициентов будут определены как
Дополнительный вопрос