R задаётся аксиоматически 5 группами аксиом:
1) 1) аксиомы сложения
· 1. x+y=z для 
x,y 
R существует единственный z 
R
· 2. (x+y)+z=x+(y+z) для 
x,y,z R
· 3. x+y=y+x для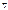 
x,y R
· 4. x+0=x для x 
R
· 5. x+x’=0 (для 
x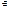 
R существует x’ 
R, противоположный x)
2) аксиомы умножения
· 1. x*y=z для x,y 
R существует единственный z R
· 2. (x*y)*z=x*(y*z) для x,y,z R
· 3. x*y=y*x для x,y R
· 4. x*1=1*x=x (1 R, 1≠0) для x R
· 5. x≠0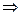 
x*x’=1 (для x,y R (x≠0) существует x’ R, x’ – обратный элемент для x)
· 3) аксиомы порядка
1. а R a≤a
2. а,b R a≤b 
b≤a 
a=b
3. а,b,с R a≤b b≤с a≤с
4)аксиомы связи
· 1. a,b,c R (a+b)*c=a*c+b*c
· 2. а,b,с R a≤b 
a+с ≤ b+с
· 3. а,b,с R (a≤b и c≥0) a*c≤b*с; (a≤b и c≤0) a*c≥b*с
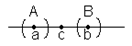Из аксиом связи вытекает плотность R, т.е. если r R и r’ R, r≤r’, то 
с R: r≤c≤r’
5) аксиома непрерывности или акс. Дедекинда:
Если А 
R и B R: а A и b B, a≤b, то 
с R: a≤c≤b
Лемма Кантора: Любая система вложенных отрезков имеет непустое пересечение.
Дано: а1≤а2≤…≤аn, b1≥b2≥…≥bn, n N
[a1,b1] 
[a2,b2]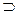 
[a3,b3] 
… [an,bn]
Доказать: с R: с пересечению системы вл-х отр.[an,bn]
Доказательство: Пусть задана система вложенных отрезков. Обозначим через А множество всех левых концов am отрезков системы, а через В – множество их правых концов bn.
Для любых номеров m и n выполняется неравенство am≤bn.
По свойству непрерывности дейст-х чисел 
с: для m,n выполняется am≤с≤bn, а значит и an≤с≤bn, n=1,2,…
След-но, т.С принадлежит всем отрезкам [an,bn], что и треб.док-ть.
Следствие: Если в сис-ме влож-х отр-ков длина отрезка→0 при n→ 
, то в пересечении будет единственная точка С.
Натуральное число – всякое число натурального ряда. Натуральный ряд – последовательность целых положительных чисел, расположенных в порядке их возрастания: 1, 2, 3, …, n, …
|
|
Всякое множество, эквивалентное мн-ву чисел натур-го ряда, наз-ся счетным. Пр.: множ-во полож-х чисел.
Натур-е числа определ-ся системой аксиом Пеано:
Натуральными числами наз-ся эл-ты непустого мн-ва N, в к-ром 
отношение «следует за», удовл-е след-м аксиомам:
1. 
число 1, не следующее ни за каким числом
2. Для числа а следующее за ним а* и притом только одно, т.е. а=b a*=b*
3. число следует не более чем за одним числом, т.е. а*=b* a=b
4. (Аксиома индукции): Пусть любое множ-во М натур-х чисел обладает свойствами:
1) единица М 2). Если число а М, то а*=а+1 также М.
Тогда М содержит все натур-е числа, т.е. мн-во N совпадает с М.
Принцип матем-й инд-ции: Если предлож-е A(n), где n N, истинно для n=1 и из предположения о том, что оно истинно для n=k, вытекает, что оно истинно для следующего числа n=k+1, то предл-е верно для любого n N.
Доказ-во, основанное на принципе МИ, наз-ся методом матем-й индук-и.
Пр-р: 12+22+32+…+n2= 
Док-м утвержд-е ММИ.
1). Для n=1 высказ-е А(1) истинно
2). Док-м, что A(k) A(k+1). Предпол-м, что рав-во верно при n=k, док-м для n=k+1:
12+22+32+…+k2+(k+1)2= 
+(k+1)2 = 
.
Упрощаем дробь. Получим 
. След-но, рав-во справедливо для n N.
Подклассы R:
N – натуральные числа{1,2,3,…}
Z – целые 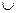= N 
N- 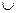{0}={…-3,-2,-1,0,1,2,3,…}
Q – { 
, m Z, n N} – рациональные
I – иррациональные числа, непредставимы в виде 
.
Любое рацион-е число представимо в виде бесконечной десятичной периодич-й дроби, а иррац-е – бескон-й десятич-й непериод-й дробью (Теория Вейерштрасса).
N Z Q R; Q 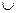I=R; A 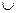T=R (А-алгебраические, Т-трансцендентные числа)
Число 
R наз-ся алгебраич-ким, если оно явл-ся корнем ур-я вида
|
|
anxn+an-1xn-1+…+a1x+a0=0, коэф-ты к-рого целые числа, не обращающиеся одновременно в 0.
Пр-1: x-5=0; 5 A Пр-2: 
; x2=2; x2-2=0; 
A
Пр-3: 
Пр-4: ех 
Т, х≠0 Пр-5: (a А, b I) ab T 
T
Множество М наз-ся счетным по мощности, если оно эквивалентно мн-ву натур-х чисел. χ0-обознач-е счетного мн-ва (это мн-ва N, Z, Q, A).
Мощность множества точек отрезка [0,1] наз-ся мощностью континуума и обозн-ся С.
Мощность континуума имеют мн-ва R, I, T.
Теория действит-х чисел возникла в сер. 19 в., когда почти одновременно были построены 3 теории действительного числа:
1). Научная школа Вейерштрасса – представление действ-го числа в виде бескон-й десятичной дроби.
2). Теория Кантора – построение фундаментальной последовательности рац-х чисел (любая фундаментальная последовательность сходится, а также принцип Архимеда: Для любых 2-х отрезков натур-е число n: произвед-е длины меньшего отр-ка на n превзойдет длину большего отр-ка).
3). Теория Дедекинда – построение сечений на мн-ве рац-х чисел. Суть метода: Мн-во Q разбив-ся на 2 неперес-ся класса А и В: 
а 
А< b B; в нижнем классе нет наибольшего числа, в верхнем – нет наименьшего. Тогда сечение (А,В), введенное таким образом на мн-ве Q определяет нек-рое иррац-е число =(А,В).
Эти 3 теории отлич-ся только аксиомами непрерывности (5-я группа аксиом).