Складывание различных предметов из геометрических фигур Дьенеша

 

Большое познавательное значение имеет складывание из гео­метрических фигур Дьенеша домиков, машинок, башен, сквореч­ников и т. п. В процессе постройки дети убеждаются, что во всем комплекте нет двух совершенно одинаковых геометрических фигур: если, например, геометрическая фигура является, голубым толстым большим кругом, то все другие большие круги или не будут толстые, или будут толстые, но другого цвета; если нужен маленький тонкий голубой треугольник, то он будет только один, другого голубого не найдется среди маленьких тонких треуголь­ников (08 приложение 1).

Некоторым детям трудно строить из неодинаковых геометри­ческих фигур Дьенеша, но есть и такие, что прекрасно справляют­ся с этим занятием. При постройке автомобиля они получают вто­рое большое толстое красное колесо путем соединения двух тонких колес той же величины, одно из которых красное (оно кладется сверху).

— Теперь кажется, что покрышки этих двух колес одинаково толстые и что оба колеса красные.

Для проверки того, насколько хорошо дети усвоили признаки геометрических фигур, был введен специальный код, графически изображающий эти признаки с помощью рисунков. С этой целью воспитательница использовала код, предложенный для дошколь­ников профессором Семадени (08 приложение 2)

Эти знаки рисуются на квадратных карточках размером 5x5 см, к каждой из которых подклеена фланель, с тем чтобы их можно было использовать на фланелеграфе.

С помощью этих знаков дети должны характеризовать приз­наки определенных геометрических фигур. Если, например, де­вочка выбрала большой голубой толстый треугольник, то в этом случае подойдет карточка с треугольником, которую она прикреп­ляет к фланелеграфу, говоря при этом:

— Это означает, что я выбрала треугольник.

Поскольку треугольник голубой, воспитательница советует ей найти и прикрепить рядом с первой карточкой карточку, вы­ражающую качество цвета, что та и делает.

— А какой еще этот голубой треугольник?

— Он большой и толстый, — определяет кто-то из детей.

Воспитательница показывает детям четыре карточки, озна­чающие величину (большой, маленький) и толщину (толстый, тонкий) геометрических фигур. Раздается смех. -Что вас так насмешило?

— Здесь нарисованы такие смешные человечки, один толстяк,
а второй такой худой, что даже живота нет. Я знаю, толстяк означает, наверное, слово «толстый», а худой человечек — кий».

- Какую же из этих четырех карточек следует прикрепить к таблице рядом с карточками, выражающими, что у нас имеется треугольник и что этот треугольник голубой? Посмотрите на гео­метрическую фигуру, которую я держу в руке.

- Толстый! Этот толстяк означает «толстый».

- Ну, так какой же является наша геометрическая фигура?

-Она является треугольником, голубым и толстым, — гово­рит Гражинка.

-Но она и большая, — дополняет Кшися. — А где карточка, которая говорит об этом?

Воспитательница показывает две карточки. На одной домик с двумя окнами и дверью, а на другой домик только с одним окном. Дети быстро догадываются, какая из карточек означает «большой», а какая — «маленький». Карточка, выражающая значение «большой», ставится на фланелеграфе около карточки со значением «толстый». Теперь Яцек «читает», глядя на фланелеграф:

— Это треугольник голубой, толстый, большой.

 

Для детей это было что-то совершенно новое. Они были уди­влены тем, что могут «прочитать», какой является выбранная геометрическая фигура. То же самое повторилось и с геометри­ческой фигурой, которая была кругом — желтым, тонким, ма­леньким.

 

Интерес к тому, что они могут «диктовать», «записывать» и «читать» про признаки геометрической фигуры, не угасал до­вольно долго. Толпясь по утрам до завтрака около таблицы, дети описывали все новые и новые геометрические фигуры с помощью принятого кода. Такими упражнениями они занимались по собственной инициативе в самое различное время.

Наконец пришло время учиться самостоятельно «записывать» признаки тех или иных геометрических фигур. Каждый ребенок получил лист бумаги, на котором была нарисована таблица, состоящая из двух строк по четыре клетки, в которых дети должны были сами рисовать знаки кода. В этот день дежурный разложил на каждом из 6 столов мелки, мешочки с логическими геометрическими фигурами, листы бумаги с таблицами.

Дидактическая игра состояла в том, что дети должны были «закодировать» и «записать» признаки геометрической фигуры, вынутой из мешочка. Воспитательница пояснила, что дети долж­ны рисовать знаки кода начиная с первой верхней левой клетки, и попросила показать эту клеточку на своих таблицах. Начались разговоры, разглядывание таблиц.

Проблемой оказалось то, что дети, сидевшие по противопо­ложным сторонам стола, видели таблицы тех, кто сидел напро­тив, как бы перевернутыми.

- Ты делаешь плохо, потому что показываешь правую кле­точку.

- Вовсе нет, правая сторона здесь, — защищаются дети, си­дящие напротив.

Воспитательница воспользовалась сложившейся ситуацией и попросила каждого отметить точкой клеточку, о которой идет речь, т. е. первую левую верхнюю.

 

Дети, сидящие друг против друга, менялись местами для того, чтобы убедиться, везде ли точка поставлена именно в первой левой верхней клеточке. Оказывалось, что везде она была по­ставлена верно.

-Так почему же вам казалось, что сидящие напротив пока­зывают неправильно? — спросила воспитательница. — Подними­те-ка теперь все левую руку. Что вы видите?

— Левая рука Гжеся находится справа от меня, а моя ле­вая рука — справа от Гани, — сказал Томек.

Не все дети поняли, почему это так, но воспитательница ре­шила продолжить объяснение позднее, во время подвижных игр, а пока вернуться к прерванному занятию.

Каждый ребенок уже знал, с какой клеточки надо начинать рисовать. Теперь появились новые сомнения:

— А если моя геометрическая фигура будет большой, то я буду должен нарисовать домик с двумя окнами и дверью, правда?

— А могу ли я нарисовать тонкого человечка немного не так, как на карточке?

— Можешь, лишь бы было ясно, что он тонкий!

— А можно закрасить всю клеточку?

— Конечно. Важно только, чтобы ты закрашивал тем же цветом, каким раскрашена твоя геометрическая фигура.

После всех этих приготовлений началась работа. Каждый по очереди вынимал из мешочка какую-нибудь одну геометрическую фигуру и внимательно рассматривал ее. Сначала каждый ребенок должен был в условленном месте с помощью кода записать, какую форму имеет выбранная им фигура. За каждым из столов двое детей громко давали определение вынутой фигуры одно­временно рисовали нужный кодирующий знак в таблице. Оши­бок не было, только одни нарисованные фигуры занимали всю клеточку, а другие были очень мелкие. Воспитательница пони­мала, что таким образом ребенок невольно определяет не только форму, но и величину геометрической фигуры, но на первый раз она не стала обращать на это внимание детей. В следующей клеточке она попросила отметить величину геометрической фи­гуры: большая или маленькая.

Неожиданно выяснилось, что детям требуется довольно много времени для того, чтобы нарисовать домик. Некоторые рисовали свои домики разноцветными, пририсовывали дымящуюся трубу, форточки, цветы на окнах. На первый раз воспитательница разрешила детям порисовать вдоволь, решив впоследствии по­степенно довести до их понимания то, что условные знаки должны быть простыми и каждый из них должен быть изображен всеми одинаково.

В третьей верхней клеточке должен быть отражен цвет гео­метрической фигуры. С этим заданием все дети справились лег­ко, самостоятельно проверив при этом друг у друга правиль­ность его выполнения.

В четвертой верхней клеточке должна быть закодирована толщина геометрической фигуры: толстая она или тонкая. Вот здесь-то стало шумно. Символы-качества, изображенные в виде людей, все еще удивляли детей. Вот один из разговоров:

— Этот должен быть тонким?

- Ведь я нарисовала, как на карточке, голову и ноги чело­вечка.

- Ну, а животик?

— Его нет, но так обозначен тонкий и на карточке, и в таб­лице.

— А я нарисовала тонкого и с тонким животиком.

Некоторые не могли поместить своих толстяков в отдельных для этого клеточках, тем не менее каждый из них мог прочи­тать, что геометрическая фигура толстая.

Закодировав признаки геометрической фигуры, дети пыта­лись читать по таблице, какой является описанная геометриче­ская фигура. Кто-нибудь из них высоко поднимал геометриче­скую фигуру и громко зачитывал описанные в таблице признаки, остальные проверяли, правильно ли была сделана запись.

— Моя геометрическая фигура квадратная, маленькая, тон­кая, красная (08 приложение 3).

Дети с интересом сравнивали признаки поднятой вверх гео­метрической фигуры с тем, что было записано в таблице.

После занятия дежурные собрали таблицы, на которых были написаны фамилии детей. Одна из таких таблиц приводится ниже (08 приложение 4).

В последующие дни воспитательница старалась вовлечь в игру прежде всего тех детей, которые в первый день отсут­ствовали, а также тех, для кого она оказалась трудной в пер­вый раз.

Игра понравилась. И в свободное время дети по своей ини­циативе охотно играли в нее. Только для этого они должны были самостоятельно приготовить для себя таблицы, в чем им на по­мощь приходила воспитательница.

Стремясь облегчить упражнения и усовершенствовать про­цесс выполнения предлагаемых заданий, воспитательница зара­нее приготовила 9 маленьких карточек размером 2,5x2,5 см со знаками кода, которыми дети могли пользоваться, не тратя вре­мени на рисование. Они сами придумывали различные способы применения геометрических форм и кода, вследствие чего со временем сложился целый ряд очень интересных игр со своими правилами. Вот, например, игра, которая проводится за одним столиком. Для нее нужны геометрические фигуры и карточки со знаками кода. Каждый по очереди выбирает себе геометриче­скую фигуру. Тот, кто первым обозначит ее (положит знаки кода перед собой), имеет право первым прочитать их.

За другим столом дети постановили, что громко прочитать свою «запись» должен именно тот, кто последним обозначил свою геометрическую фигуру. При этом часто можно было таким об­разом обнаружить ошибки или непонимание какого-либо знака. Самыми неоднородными оказались знаки, используемые для кодирования признака «большой» — «маленький».

На последнем этапе игра проводилась уже в следующем варианте: каждый из играющих, закодировав признаки своей геометрической фигуры, оставлял ее рядом с кодом, а сам вста­вал с места, пересаживался, например, на два места вправо и сравнивал оказавшуюся перед ним геометрическую фигуру с ле­жащим рядом с ней кодом, проверяя, не допущена ли там какая-либо ошибка.

Таким образом дети научились свободно пользоваться кодом. Это позволило ввести знак отрицания «не», который в рисуноч­ном коде выражается перечеркиванием крест-накрест соответству­ющего кодирующего рисунка.

Сочетание знака кода и отрицания «не» может быть связано с различной степенью сложности его, раскодирования. Легче всего понять такой знак, выбрав единственно возможный проти­воположный признак, в том случае, когда выбор осуществляется только между двумя признаками, например между «большой» — «маленький», «толстый» — «тонкий». В этом случае (08 приложение 5)

Легко использовать знаки отрицания в игре «Угадай, какой кубик».

За столом сидят несколько ребят. На середине стола лежат приготовленные карточки с кодом. В закрытой коробке находят­ся знаки отрицания того или иного значения признака величины, а именно:

 

 

Для этой игры с теми же знаками отрицания были приготов­лены и карточки большего размера, к которым была приклеена фланель, позволяющая использовать их на фланелеграфе.

Воспитательница говорит:

—Я скажу вам, какая у меня имеется геометрическая фигура, а вы опишите ее, кладя перед собой одновременно все карточки с необходимыми знаками. Внимание! У меня круг. — Все дети кладут перед собой знак продиктованной формы.

—Он желтый. — Дети кладут карточки, означающие приз­нак цвета.

—Он тонкий. — Воспитательница проверяет, не ошибся ли кто-нибудь.

—Он не. является большим! — Дети смотрят на карточку, которую показывает воспитательница.

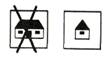Здесь нарисован знак «большой», но он перечеркнут крест-
накрест. Это перечеркивание означает отрицание «не» — «не большой». Если круг не является большим, то каким он может быть?

—Маленьким!

—Правильно, и поэтому рядом со знаком «не большой» по­местим знак «маленький».

 

 

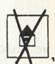Показывая карточку со знаком «не маленький»

воспитательница просит детей прочитать, что он означает.

— Не маленький, — читают дети.

— Ну, тогда что же означает этот знак?

— Большой!

 

 

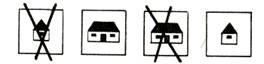Воспитательница прикрепляет к таблице обе карточки со знаками.

 

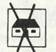После этого дети открывают коробочку, в которой находятся маленькие карточки со знаками отрицания — все перечеркнутые. По очереди вынимая карточки, они читают: «не большой», «не маленький», «не маленький», «не большой» и т.д.

 

 

- Что означает этот знак?

— Не большой.

— Так какой же?

 

 

— Маленький.

 

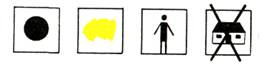
Дети читают знаки отрицания и определяют альтернативные значения признака величины:

- Круг желтый, тонкий, не большой, т. е. маленький, — после чего проверяют, действительно ли имеющаяся геометрическая фигура является желтым тонким маленьким кругом.

 

В последующие дни дети уже по собственной инициативе занимались тем, что выбирали геометрические фигуры и описы­вали их, например:

— Это квадрат, голубой, толстый, — небольшая заминка,— не маленький (поскольку квадрат был большим).

После этого было легко ввести знак отрицания большой тол­щины, поскольку в этом случае также имеется только одна альтернатива: толстый или тонкий. Если геометрическая фигура не является толстой, то она тонкая, если не является тонкой, то — толстая.

В игре можно теперь использовать знак отрицания и двух значений признака величины, и двух значений признака толщины. Определяя, например, красный, не толстый, не маленький тре­угольник, дети укладывали при этом карточки с соответствующи­ми знаками и приговаривали:

— Этот треугольник не толстый, — значит, тонкий, не малень­кий, — значит, большой. — После этого под первым рядом кар­точек укладывался второй ряд, в котором знаки отрицания были
заменены знаками, выражающими соответствующие значения признаков толщины и величины.

 

На следующее утро, придя в детский, сад, до завтрака дети толпились у фланелеграфа и определяли признаки выбранной геометрической фигуры, используя при этом и знаки отрицания признаков величины и толщины. Конечно, не обходилось без ошибок, но всегда рядом находились дети, которые могли испра­вить ошибку.

 

Игра с использованием знаков отрицания становится особен­но сложной в том случае, когда знак отрицания относится к признаку цвета. В этом случае возможны две альтернативы: если не красный, то может быть как желтый, так и голубой. Тут детям сложно понять, о чем идет речь. Большая сосредоточенность вни­мания требовалась при выборе надлежащих карточек и прочитывании их:

 

— Не красный, следовательно, голубой или желтый.

— Не голубой, следовательно, красный или желтый.

— Не желтый, следовательно, красный или голубой.

 

Набор карточек обогатился теперь знаками отрицания каж­дого из трех цветов.

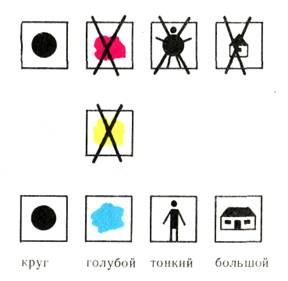
При таком усложненном варианте игры уже было недостаточ­но просто выразить словами значение карточки со знаком отри­цания определенного цвета, например «не красный», и поло­жить ее на стол — ведь это мог быть или желтый, или голубой цвет. В игре используется еще один элемент, например вопрос: не желтый ли? Если ответ на этот вопрос отрицателен, то оп­ределяемая геометрическая фигура является голубой: ведь если она не красная и не желтая, то она может быть только голубой. Это уже типичный логический вывод, сделанный ребенком, т.е. свидетельство его умения логически мыслить.

В конце игры картинки с кодом оказались положенными сле­дующим образом:

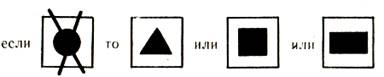
Аналогично вводится отрицание формы. Игра проводится так же, но с учетом наличия четырех видов геометрических форм. Здесь приходится сталкиваться уже с тремя альтернативами: если та или иная геометрическая фигура «не круг», то это может быть либо треугольник, либо квадрат, либо прямоугольник:

 

Здесь потребуется задать уже не один вопрос, а несколько, чтобы уточнить форму той или иной геометрической фигуры, в отличие, например, от случая определения цвета.

Игра проходит следующим образом. Воспитательница прячет ладони какую-либо геометрическую фигуру и спрашивает:

-Фигура, какой формы находится у меня в руке? Кто-либо из ребят задает встречный вопрос:

— Не треугольник ли это?

-Нет. Дети кладут перед собой на стол карточку со знаком

 

«не треугольник».

— Может быть, это прямоугольник?

— Нет.

 

 

Дети кладут карточку со знаком «не прямоугольника под карточкой «не треугольник». - Может быть, это круг? - Нет

Под карточкой со знаком отрицания прямоугольника дети кладут карточку со знаком отрицания круга. Воспитательница помогает им, обращаясь с просьбой прочитать по карточкам, чем же не является ее геометрическая фигура. Дети читают гром­ко вслух:

-Не является треугольником, не является прямоугольником, не является кругом.

И здесь Галинка вскрикивает:

- Но ведь это квадрат!

 

-Найдите карточку со знаком квадрата ее под карточкой со знаком «не круг». Потом воспитательница говорит:

- Моя геометрическая фигура не желтая. — Дети кладут рядом с карточкой отрицания треугольника карточку со знаком отрицания желтого цвета

 

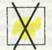
Может быть, ваш квадрат красный? Нет.

Дети кладут карточку с отрицанием красного цвета под карточкой с отрицанием желтого цвета.

Яцек шепчет:

- Не желтый, не красный, но ведь тогда он голубой! Ко­нечно, он голубой!— и кладет карточку со знаком «голубой» рядом с карточкой со знаком квадрата.

Воспитательница говорит:

— Мой квадрат толстый. — Дети несколько удивленно берут карточку со значением «толстый» и кладут ее рядом с кар­точкой «голубой». Теперь они сами интересуются: большой ли квадрат?

— Нет, — отвечает воспитательница, и дети сами делают не­обходимый вывод и кричат почти хором:

— Ну, тогда он маленький.

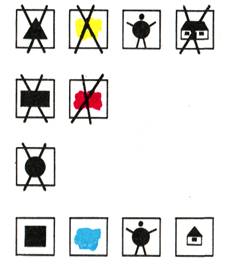Рядом с карточкой со значением «толстый» кладется карточ­ка со значением «маленький».

Теперь легко прочитать все признаки угадываемой геометриче­ской фигуры: это квадрат, голубой, толстый, маленький.

Вышеописанные игры очень любимы детьми и весьма полезны с познавательной точки зрения. Они способствуют выработке умения правильно определять признаки геометрических фигур и пользоваться кодом. Теперь уже можно перейти к играм, опи­сание которых дается в инструкции, прилагаемой к набору геометрических фигур, предназначенных для развития логиче­ского мышления (для дошкольников).