Лабораторная работа 7.
Множественная линейная регрессия: прогнозирование.
Одна из важнейших задач эконометрического моделирования – прогнозирование, т.е. оценка значения эндогенного показателя при заданных значениях экзогенных переменных. Различают прогноз среднего значения, т.е.  , где
, где  - значения экзогенных переменных, и прогноз индивидуального значения, т.е.
- значения экзогенных переменных, и прогноз индивидуального значения, т.е.  , где ε0 – случайная величина.
, где ε0 – случайная величина.
Задание 1. Построить точечный прогноз стоимости квартиры, если общая площадь totsp =55.
Указание. Точечный прогноз получается простой подстановкой значений экзогенных переменных в уравнение линейной регрессии, т.е. если значения экзогенных переменных равны  , то прогнозное значения эндогенного показателя равно
, то прогнозное значения эндогенного показателя равно 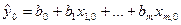 .
.
Для построения прогноза будем использовать модель парной линейной регрессии с переменной totsp. Уравнение модели имеет вид 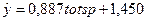 (см. лабораторную работу 3). Подставляя в это уравнение значение totsp = 55, получим
(см. лабораторную работу 3). Подставляя в это уравнение значение totsp = 55, получим  . Следовательно,
. Следовательно,  и Y 0 » 47,3
и Y 0 » 47,3
Доверительное прогнозирование
Доверительный (интервальный) прогноз представляет собой промежуток, который накрывает прогнозируемое значение с заданной доверительной вероятностью (уровнем надежности).
Задание 2. Построить доверительный прогноз средней стоимости квартиры, если totsp =55.
Указание. Для построения прогноза будем использовать модель парной линейной регрессии с переменной totsp.
Шаг 1. Построить матрицу наблюдений X следующего вида:
 , где
, где  - наблюдаемые значения показателя
- наблюдаемые значения показателя 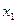 и т.д.
и т.д.
Для рассматриваемой модели, это матрица размерности 20 на 2 (в первом столбце 1, во втором – наблюдаемые значения totsp).
Шаг 2. Вычислить матрицу коэффициентов системы нормальных уравнений XTX, где  - это транспонированная матрица X. Размер матрицы, полученной умножением двух матриц, определяется количеством строк первой матрицы
- это транспонированная матрица X. Размер матрицы, полученной умножением двух матриц, определяется количеством строк первой матрицы  и количеством столбцов во второй матрице X. В нашем случае, матрица XTX имеет размер 2x2. Транспонированную матрицу
и количеством столбцов во второй матрице X. В нашем случае, матрица XTX имеет размер 2x2. Транспонированную матрицу  можно найти с помощью функции из категории Ссылки и массивы:
можно найти с помощью функции из категории Ссылки и массивы:
ТРАНСП(массив), где массив — диапазон ячеек, который нужно транспонировать.
Для вычисления произведения матриц используйте следующий оператор из категории Математические: МУМНОЖ(массив1; массив2), где
· массив1 — первый из перемножаемых массивов значений,
· массив2 — второй из перемножаемых массивов значений.
В нашем случае массив1 – это транспонированная матрица. Таким образом, матрицу  можно вычислить с помощью следующей функции:
можно вычислить с помощью следующей функции:
МУМНОЖ(ТРАНСП(массив); массив),
· массив — массив значений, соответствующей матрице наблюдений.
| 952,6 | |
| 952,6 | 46260,46 |
Для получения требуемой матрицы необходимо ввести последнюю функцию как функцию массива. Результат вычисления приведен в таблице.
Шаг 3. Найти ковариационную матрицу B оценок наименьших квадратов коэффициентов уравнения bm, …, b 0, т.е. матрицу вида
 .
.
Ковариационная матрица может быть найдена с помощью следующего равенства: 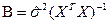 , где
, где  - оценка остаточной дисперсии. Для нахождения матрицы
- оценка остаточной дисперсии. Для нахождения матрицы 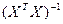 , обратной к
, обратной к  - нужно использовать функции из категории Математические:
- нужно использовать функции из категории Математические:
МОБР(массив), где массив — массив, для которого нужно вычислить обратную матрицу
| 30,21885 | -0,62227 |
| -0,62227 | 0,013065 |
Функция МОБР() также является функцией массива. Обратная матрица имеет ту же размерность, что и исходная матрица, т.е. в нашем случае 2x2. Величину  можно найти среди значений, полученных с помощью функции ЛИНЕЙН(…) или в отчете по регрессии (см.работы 3 и 4). Проверьте, что полученная матрица B совпадет с приведенной.
можно найти среди значений, полученных с помощью функции ЛИНЕЙН(…) или в отчете по регрессии (см.работы 3 и 4). Проверьте, что полученная матрица B совпадет с приведенной.
| X0(трансп) | X0 | ||
Шаг 4. Найти дисперсию прогноза среднего значения  , где
, где  - вектор-столбец вида
- вектор-столбец вида 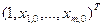 , составленный из заданных значений объясняющих переменных
, составленный из заданных значений объясняющих переменных  ,
,  - соответственно, вектор-строка (см. таблицу). Для вычисления дисперсии
- соответственно, вектор-строка (см. таблицу). Для вычисления дисперсии  используйте функцию МУМНОЖ().
используйте функцию МУМНОЖ().
Шаг 5. Построить доверительный интервал вида  , где t (кр)= tα (df) - двусторонняя критическая точка распределения Стьюдента с числом степеней свободы равным
, где t (кр)= tα (df) - двусторонняя критическая точка распределения Стьюдента с числом степеней свободы равным
df = (n-m-1). Проверьте, что при уровне надежности 0,95 нижняя граница доверительного прогноза  составит 44,9, а верхняя граница
составит 44,9, а верхняя граница 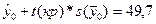
Задание 3. Постройте доверительный прогноз для стоимости квартиры, если totsp =55.
Указание. Доверительный интервал для индивидуального значения эндогенного показателя имеет следующий вид:
 ,
,
где  - дисперсия прогноза индивидуального значения. Проверьте, что можно гарантировать с уровнем надежности 0,95, что стоимость квартир общей площадью totsp =55 будет принимать значения от 39,8у.е. до 54,9у.е.
- дисперсия прогноза индивидуального значения. Проверьте, что можно гарантировать с уровнем надежности 0,95, что стоимость квартир общей площадью totsp =55 будет принимать значения от 39,8у.е. до 54,9у.е.