Свойства от синусоидальной спирали

· Точка, где лемниската пересекает саму себя, называется узловой или двойной точкой.

· Касательные в двойной точке составляют с отрезком F ₁ F ₂ углы .

· Угол μ, составляемый касательной в произвольной точке кривой с радиус-вектором точки касания равен .

· Касательные в точках пересечения кривой и хорды, проходящей через двойную точку, параллельны друг другу.

· Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу.

· Радиус кривизны лемнискаты есть

Есть частный случай формулы радиуса кривизны синусоидальной спирали:

 

при m = 2,

 

однако, легко вывести и по определению.

Уравнение лемнискаты в полярной системе:

Формулы перехода к полярной системе координат:

 

 

Выражаем :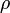

 

 

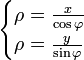
Подставляем в уравнение лемнискаты и выражаем x и y:

 

—- это параметрическое уравнение относительно . Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно , указанное выше в разделе Уравнения.

Формула радиуса кривизны кривой, заданной параметрически:

 

 

Находим производные по :

 

 

 

 

 

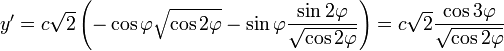
Подставляем в формулу радиуса:

 

 

Возвращаемся к уравнению лемнискаты:

 

Подставляем это выражение в полученную формулу радиуса и получаем:

 

 

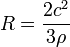
· Натуральное уравнение кривой имеет вид

 

 

· Подерой лемнискаты является синусоидальная спираль

 

 

· Лемниската сама является подерой равносторонней гиперболы.

Собственные свойства:

Гравитационное свойство лемнискаты

· Кривая является геометрическим местом точек, симметричных с центром равносторонней гиперболы относительно её касательных.

· Отрезок биссектрисы угла между фокальными радиус-векторами точки лемнискаты равен отрезку от центра лемнискаты до пересечения её оси с этой биссектрисой.

· Материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол 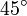с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.

· Площадь полярного сектора 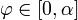, при :

 

 

o В частности, площадь каждой петли , то есть площадь, ограниченная кривой, равна площади квадрата со стороной .

· Перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо её точки, делит площадь соответствующего сектора пополам.

· Длина дуги лемнискаты между точкам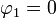и и выражается эллиптическим интегралом рода:

·

где

 

o В частности, длина всей лемнискаты

 

 

 

Приложение

 

В геометрии, синусоидальная спираль — семейство кривых, определяемое уравнением в полярной системе координат:

 

rⁿ = aⁿ cos(n θ),

 

где a — ненулевая константа и n — рациональное число, не равное нулю. С учетом возможности поворота кривой относительно начала координат уравнение также может быть записано в виде:

 

rⁿ = aⁿ sin(n θ)

 

Использование термина «спираль» в данном случае не является точным, т. к. получаемые кривые по форме скорее напоминают цветок. Многие известные кривые являются частными случаями синусоидальной спирали:

· Прямая (n = −1)

· Окружность (n = 1)

· Гипербола (n = −2)

· Парабола (n = −1/2)

· Кардиоида (n = 1/2)

· Лемниската Бернулли (n = 2)

Впервые была изучена Маклореном.