ПЛАКАТ 1,2,
Лекция 4.
Сдвиг и кручение
Сдвиг
Чистым сдвигом называют такое напряженное состояние, когда на гранях элементарного параллепипеда действуют только касательные напряжения. Такие грани называют площадками чистого сдвига.
ПЛАКАТ 3
Если нагрузить брус, как показано на рисунке, то при определенной величине сил F произойдет срез – разделение бруса на 2 части по сечению АВ. Срезу предшествует перекашивание прямых углов параллелепипеда abcd – эту деформацию называют сдвигом. Величина S – называется абсолютным или линейным сдвигом. Она зависит от размера «а». Величина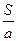 
называется относительным сдвигом. Угол g - называется углом сдвига. Так как в пределах упругой деформации угол g очень мал, то можно записать:
tg g= 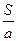» g (1)
При чистом сдвиге в поперечных сечениях возникает только один ВСФ – поперечная сила Fy (Qy).
Касательные напряжения определяются соотношением:
t=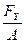 
(2)
где А – площадь поперечного сечения.
Закон Гука при чистом сдвиге имеет вид (3)
ПЛАКАТ 4
Модули упругости первого и второго рода связаны между собой соотношением (4).
На срез рассчитываются заклепочные, сварные, шпоночные и шлицевые соединения.
Кручение
ПЛАКАТ 5
Кручением называется такое напряженное состояние, при котором в поперечном сечении вала возникает только один ВСФ – крутящий момент MZ (ТК). Крутящий момент является моментом внутренних сил упругости и численно равен моменту внешних сил, действующих по одну сторону сечения. Его величину определяют методом сечений.
Положительным направлением момента будем считать такое, при котором внешние моменты вращают отсеченную часть против часовой стрелки, если смотреть со стороны сечения.
|
|
Наглядное представление о величине MZ в любом сечении вала дают эпюры крутящих моментов.
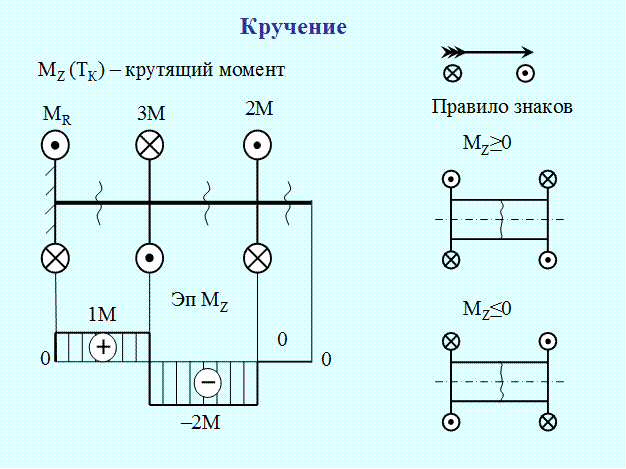
Величина MZ в сечении заделки равна MR – моменту реакции заделки – реактивному моменту.
На эпюре моментов в местах приложения сосредоточенных моментов имеются скачки равные этим моментам.
Если на цилиндр нанести прямоугольную сетку из окружностей и образующих, то после приложения внешнего момента Т прямоугольники превратятся в параллелограммы, окружности поворачиваются вокруг оси, а образующие становятся винтовыми линиями.
ПЛАКАТ 6
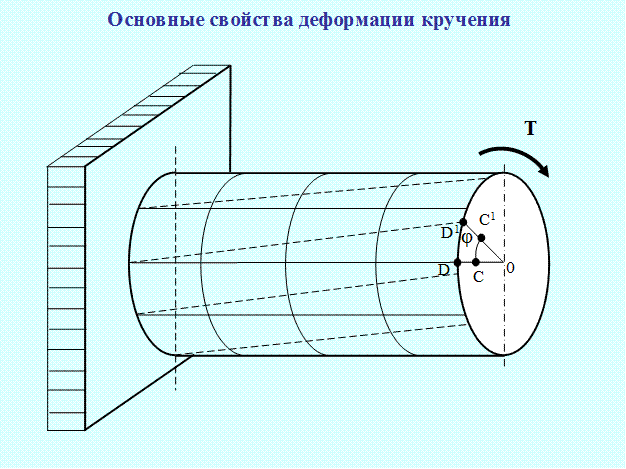
Это наблюдение позволяет сделать следующие выводы об основных свойствах деформации кручения в пределах упругости:
а) Ось кручения (вала) не деформируется;
б) Поперечные сечения при кручении поворачиваются как жесткие диски;
в) Равноотстоящие поперечные сечения поворачиваются на равные углы. Угол поворота концевого сечения называют полным углом закручивания и обозначают через φ;
г) В поперечных и продольных сечениях возникают только касательные напряжения;
д) В пределах упругих деформаций длину вала можно считать постоянной;
е) Точка D переместится по дуге DD1, а точка С по меньшей дуге СС1, следовательно абсолютная деформация (сдвиг) и напряжения зависят от радиуса.
Определение напряжений при кручении
ПЛАКАТ 7
Для установления закона распределения касательных напряжений по поперечному сечению скручиваемого стержня, рассмотрим более детально деформацию стержня на участке dz.
Угол сдвига γ образующей цилиндра радиусом ρ равен:
|
|
Касательные напряжения по закону Гука при сдвиге (9).
ПЛАКАТ 8
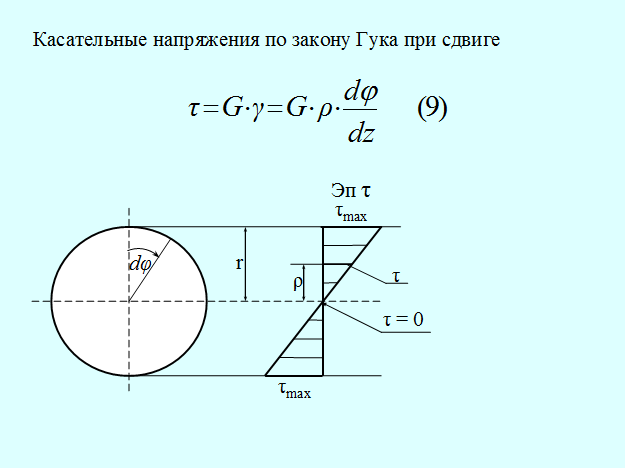
Из (8) и (9) следует, что при кручении деформации сдвига и касательного напряжения прямо пропорциональны расстоянию от центра тяжести сечения.
В центре тяжести τ = 0 и τ = τмах у поверхности стержня.
Зная закон распределения касательных напряжений, легко определить их величину из условия, что крутящий момент в сечении, представляет собой равнодействующий момент касательных напряжений в сечении (10).
где τ·ρ·dA – элементарный крутящий момент внутренних сил, действующих по площадке dA.
ПЛАКАТ 9
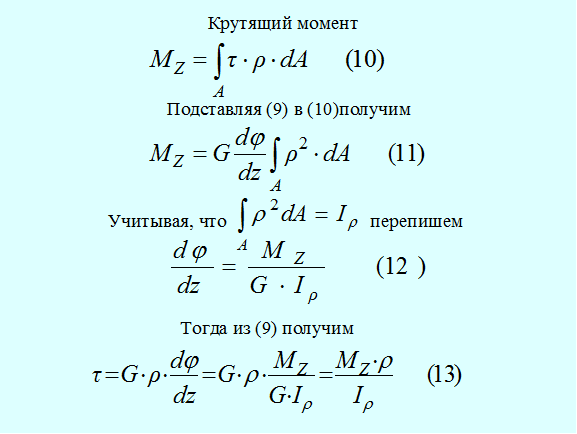
Из (13) следует, что в точках, одинаково удаленных от центра тяжести сечения, касательные напряжения τ одинаковы.
ПЛАКАТ 10
ПЛАКАТ 11
Деформации и перемещения при кручении
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:
ПЛАКАТ 12
