Метод конечных элементов (МКЭ)
Основные понятия МКЭ, обозначения и соотношения.
Основная идея метода: аппроксимация сплошной среды с бесконечным числом степеней свободы, совокупностью простых элементов с конечным числом степеней свободы и связанных в узловых точках.
Основные принципы МКЭ
Предположим, что мы решаем задачу теории упругости в перемещения (очевидно, что неизвестными являются перемещения во всех точках тела).
Первый этап: построение сетки – аппроксимация исходной области набором простых по форме подобластей (конечных элементов) 
. Замена не точна. КЭ связаны друг с другом в некоторых точках, расположенных на их границах – узлах КЭ. Основными неизвестными считаются перемещения этих точек (узлов).
Второй этап: Выбирается система функций, однозначно определяющих неизвестные (перемещения) внутри КЭ, через неизвестные в узлах КЭ – функции формы. Поля неизвестных внутри элемента аппроксимируются через неизвестные в узлах КЭ.
Третий этап: С использованием соотношений ТУ через введённые аппроксимации полей перемещений определяются деформации, а затем и напряжения в любой точке КЭ. В результате деформации и напряжения внутри КЭ оказываются выражены через перемещения узлов КЭ.
Четвёртый этап: Записываются условия равновесия системы КЭ, отражающие тот факт, что система внутренних сил упругости, приведённых к узлам КЭ, должна уравновешивать систему внешних сил, приведённую к узлам сетки. Условия равновесия записываются в жёсткостной форме и представляют собой СЛАУ относительно перемещений в узлах сетки. Проще говоря, учитывается физическая сторона решаемой задачи будь-то ТУ или другой.
|
|
Рассмотрим пример построения матричной формы записи векторных и тензорных соотношений на примере постановки плоской задачи ТУ (рисуем тело с указанием возможных сил и ГУ как статических, так и кинематических).
, 
,
, ,
, ,
, 
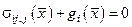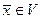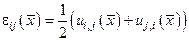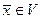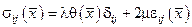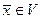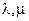– параметры Ламе.
, 
,
.
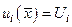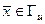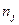– компоненты вектора внешней единичной нормали (направляющие косинусы).
Строим сетку и на ней вводим векторные и матричные соотношения для треугольного трёхузлового КЭ.
.
, 
.
Здесь 
– номер элемента внутри сетки.
, где 
.
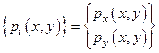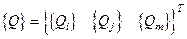, где 
.
, где 
.
,
.
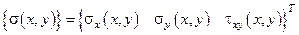Задаём аппроксимацию перемещений внутри элемента:
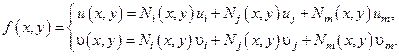
Здесь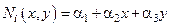 
– функция формы КЭ.
Ф.ф. должны обеспечивать непрерывность поля перемещения на границах КЭ.
, где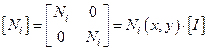 
и т.д.
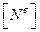– матрица ф.ф. КЭ.
Тогда
.
Из соотношения Коши (геометрич.) имеем
.
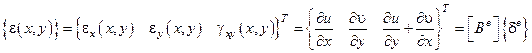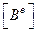– матрица градиентов, которая связывает деформации и перемещения.
, где 
и т.д.
Из закона Гука (физ. соотн.)
.
– матрица упругих констант, связывает напряжения и деформации.
.
Тогда
.
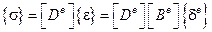В общем случае
, где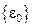 
– свободные деформации (температурн.)
Принцип возможных перемещений.
Рассмотрим малое возможное поле перемещений, не противоречащее ГУ –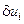 
.
Тогда
, ,
.
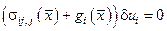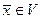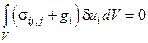Рассмотрим
,
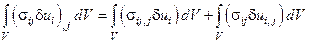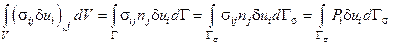(Остроградского).
По теореме Гаусса–Остроградского
.
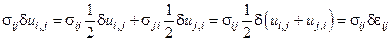Тогда
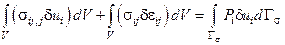, где 
.
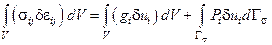или
.
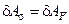Итак, работа внутренних сил равна работе внешних сил на возможных перемещениях.
Вывод КЭ соотношений из принципа возможных перемещений.
Рассмотрим отдельный элемент (рисуем его).
.
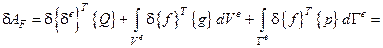
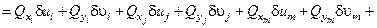
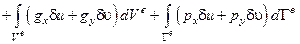Здесь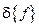 
– вариация вектора перемещений 
.
Мы знаем, что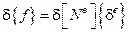 
и 
. Тогда
.
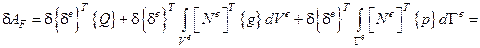
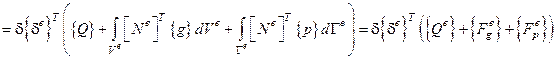Это была работа внешних сил на возможных перемещениях.
, где 
.
Теперь работа внутренних упругих сил:
|
|
.
.
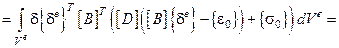
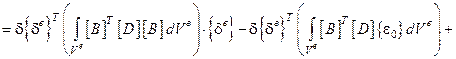
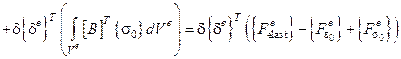– матрица жёсткости – квадратная, симметричная, положительно определённая.
Зная, что 
, получаем
,
,
Очевидно – 
!
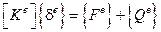, откуда
.
Записывая условия равновесия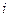 
-го узла всей системы КЭ имеем
, 
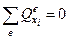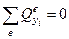. Тогда 
по всем элементам!
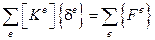или для всей системы 
– СЛАУ МКЭ (состоит из глобальной матрицы и векторов)!
Это и есть жёсткостная форма записи МКЭ. Для решения необходимо учесть кинематические ГУ, иначе система будет иметь нулевой определитель!