Для многослойных структур характерна высокая прочность композита в плоскости слоев и, как правило, низкая прочность между слоями. Поэтому эти материалы имеют большое преимущество, когда напряжения в слоях значительно превышают межслоевые нормальные и касательные напряжение. В этом случае координаты 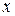 ,
, 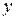 и
и 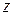 являются неравноправными. Если координату
являются неравноправными. Если координату 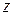 направить по нормали к поверхности приведения и попытаться отделить эту координату, то можно свести трехмерные исходные уравнения к двумерным. Это можно сделать как формально математически, так и с помощью введения гипотез. Если в уравнения равновесия ввести безразмерные координаты
направить по нормали к поверхности приведения и попытаться отделить эту координату, то можно свести трехмерные исходные уравнения к двумерным. Это можно сделать как формально математически, так и с помощью введения гипотез. Если в уравнения равновесия ввести безразмерные координаты 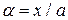 ,
, 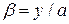 ,
, 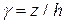 , то согласно этим уравнениям межслоевые касательные напряжения
, то согласно этим уравнениям межслоевые касательные напряжения 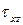 и
и 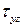 будут порядка
будут порядка 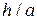 от величины нормальных напряжений, а нормальные напряжения
от величины нормальных напряжений, а нормальные напряжения 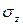 будут соизмеримы с величиной
будут соизмеримы с величиной 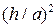 от величин
от величин 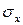 и
и 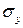 . Этот анализ показывает, что чем меньше относительная толщина пластина, тем меньше напряжения, действующие на площадках, нормальных к оси
. Этот анализ показывает, что чем меньше относительная толщина пластина, тем меньше напряжения, действующие на площадках, нормальных к оси 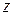 . В элементах, где все компоненты напряжения соизмеримы между собой, волокнистые композиты утрачивают свою эффективность как силовые конструкционные материалы.
. В элементах, где все компоненты напряжения соизмеримы между собой, волокнистые композиты утрачивают свою эффективность как силовые конструкционные материалы.
Получим разрешающее уравнение изгиба многослойных композитных пластин с учетом поперечного сдвига из-за податливости связующего между слоями по толщине. Примем, что суммарное смещение (рис. 5.1,в) изгибаемых систем складывается из чистого изгиба (рис. 5.1,а), связанного с поворотом поперечного сечения, и чистого сдвига (рис. 5.1,б) без поворота нормального элемента. Для оценки влияния сдвига при изгибе не будем учитывать особенности структуры, а будем рассматривать пластину с симметричной укладкой по толщине слоев. При выводе разрешающих соотношений задачи обжатием по толщине пренебрежём.
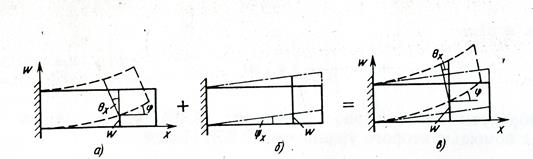
Рис.5.1. Смещение сечения балки, вызванное изгибом (а), сдвигом (б),
изгибом со сдвигом (в)
Как было показано в четвертый главе, в случае выполнения условия отсутствия сдвига по толщине 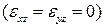 перемещения в плоскости определяются соотношениями
перемещения в плоскости определяются соотношениями 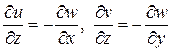 . В случае учета сдвига эти перемещения определяются выражениями
. В случае учета сдвига эти перемещения определяются выражениями
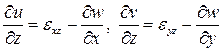 . (5.1)
. (5.1)
Имея в виду, что толщина пластинки сравнительно мала, представляется возможность осреднить деформации 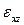 и
и 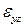 по толщине, т. е. заменить истинные деформации
по толщине, т. е. заменить истинные деформации 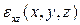 и
и 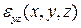 некоторыми осредненными по толщине деформациями сдвига
некоторыми осредненными по толщине деформациями сдвига
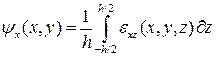 и
и 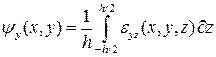 . (5.2)
. (5.2)
Тогда соотношения (5.1) с учетом (5.2) можно переписать в виде
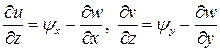 .
. 
 (5.3)
(5.3)
Интегрируя эти выражения, получаем
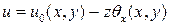 и
и 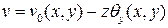 ,
,
где 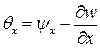 и
и 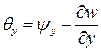 .
.
Таким образом, видно (см. рис. 5.1), что при учете деформации сдвига для определения углов поворота сечения 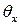 и
и 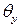 из полного угла поворота
из полного угла поворота 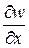 или
или 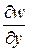 необходимо вычесть угол сдвига
необходимо вычесть угол сдвига 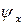 или
или 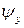 , так как при сдвиге прогиб балки не сопровождается поворотом сечения.
, так как при сдвиге прогиб балки не сопровождается поворотом сечения.
К полученным ранее выражениям, используемым при выводе разрешающего уравнения изгиба пластин в соответствии с гипотезой Кирхгофа, добавим следующие соотношения:
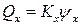 ;
; 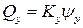 ;
; 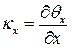 ;
; 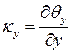 ;
; 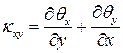 .
. 
Здесь 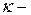 кривизны;
кривизны; 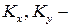 обобщенные жесткости, учитывающие жесткость при трансверсальном сдвиге. Определим эти жесткости. Для непрерывно меняющихся по толщине параметрах физические соотношения для сдвига запишутся в виде
обобщенные жесткости, учитывающие жесткость при трансверсальном сдвиге. Определим эти жесткости. Для непрерывно меняющихся по толщине параметрах физические соотношения для сдвига запишутся в виде
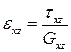 ,
, 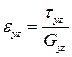 . (5.4)
. (5.4)
Перерезывающие силы определяются интегрированием 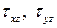 по толщине, т.е.
по толщине, т.е.
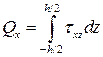 ,
, 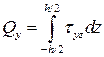 .
.
Используя выражения (5.2) и исключая деформацию сдвига с помощью соотношений (5.4), записываем
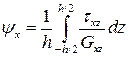 ,
, 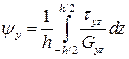 (5.5)
(5.5)
В подынтегральном выражении заменим 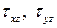 на осредненные по толщине значение сдвиговых напряжений
на осредненные по толщине значение сдвиговых напряжений 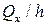 и
и 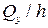 . Тогда выражения (5.5) примут вид
. Тогда выражения (5.5) примут вид
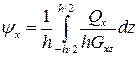 ,
, 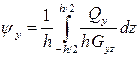 .
.
Переходя от непрерывности интеграла по 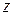 к суммированию по слоям, получаем
к суммированию по слоям, получаем
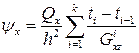 ,
, 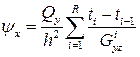
или
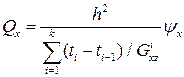 ,
, 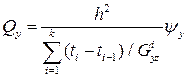 .
.
Сравнивая эти соотношения с аналогичными в выражениях (5.4), получаем
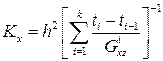 ,
, 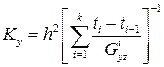 . (5.6)
. (5.6)
Здесь при вычислении жесткостей отсчет слоев ведется от одной из поверхностей пластины, 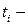 расстояние от поверхности до нижней границы
расстояние от поверхности до нижней границы 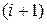 -го слоя, поэтому
-го слоя, поэтому 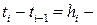 толщина
толщина 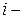 го слоя;
го слоя; 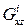 и
и 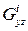 - модуль поперечного сдвига
- модуль поперечного сдвига 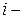 го слоя.
го слоя.
Используя уравнения равновесия изгиба пластин, физические и геометрические соотношения с учетом выражений (5.3), разрешающие уравнения получаем в виде
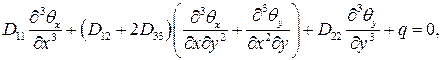
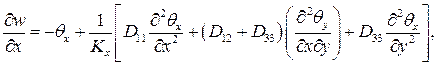 (5.7)
(5.7)
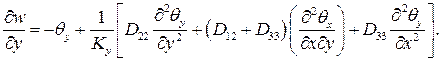
Здесь изгибаемые жесткости имеют традиционный вид. Если не учитывать деформацию поперечного сдвига, приняв 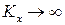 и
и 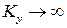 , то тогда
, то тогда 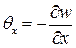 ,
, 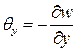 , и уравнение (5.7) принимает классический вид для ортотропной пластины в соответствии с гипотезой Кирхгоффа.
, и уравнение (5.7) принимает классический вид для ортотропной пластины в соответствии с гипотезой Кирхгоффа.
Рассмотрим решение задачи для случая шарнирного опирания пластины по краям. В этом случае искомые функции представляются в виде
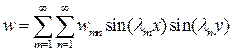 ;
; 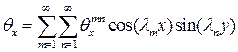 ;
;
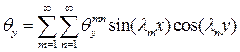 ;
; 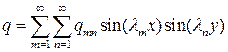 ,
,
где 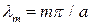 ,
, 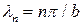 .
.
После подстановки рядов в систему (5.7) и приравнивания коэффициентов при одинаковых комбинациях тригонометрических функций, получим следующую систему уравнений:
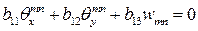 ;
;
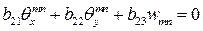 ;
;
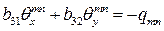 ,
,
где 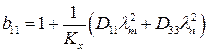 ;
; 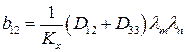 ;
; 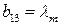 ;
;
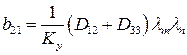 ;
; 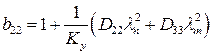 ;
; 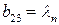 ;
;
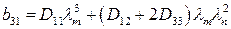 ;
; 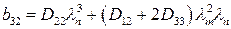 ;
;
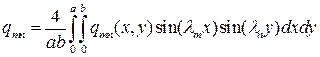 .
.
Тогда решение этой системы записывается в форме
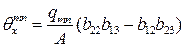 ;
; 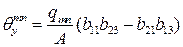 ;
;
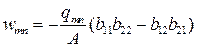 ;
; 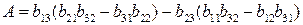 . (5/8) (5.8)
. (5/8) (5.8)
Без учета сдвига, когда 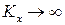 и
и 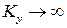 , а коэффициенты равны
, а коэффициенты равны 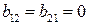 и
и 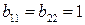 функция прогиба имеет вид
функция прогиба имеет вид
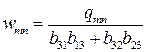 . (5.9)
. (5.9)
или 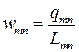 ,
,
где 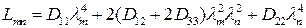 .
.
Проиллюстрируем влияние межслойного сдвига на прогиб на примере многослойной композиционной пластины квадратной в плане со стороной 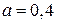 м. Обшивка толщиной
м. Обшивка толщиной 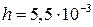 м образована на чередующихся слоях углепластика с углами армирования
м образована на чередующихся слоях углепластика с углами армирования 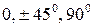 . Изгибаемая пластина обладает следующими жесткостями:
. Изгибаемая пластина обладает следующими жесткостями: 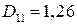 кН∙м;
кН∙м; 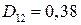 кН∙м;
кН∙м; 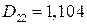 кН∙м;
кН∙м; 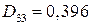 кН∙м;
кН∙м; 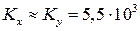 кН/м. Поперечная нагрузка на поверхности пластины имеет вид
кН/м. Поперечная нагрузка на поверхности пластины имеет вид 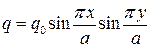 кН∙м.
кН∙м.
Максимальный прогиб пластины, вычисленный с учетом поперечного сдвига по формуле (5.8) равен 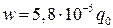 м, а прогиб, вычисленный без учета поперечного сдвига равен
м, а прогиб, вычисленный без учета поперечного сдвига равен 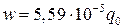 м.
м.
Учет поперечного сдвига существенен для трехслойных панелей, у которых жесткие несущие внешние слои разнесены с помощью легкого заполнителя. В этом случае для расчета можно использовать приведенные формулы. Например, для трехслойной шарнирно опертой балки, состоящей из несущих дюралюминиевых слоев толщиной 10-3 м и легкого заполнителя с модулем сдвига 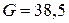 МПа, толщиной
МПа, толщиной 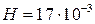 м и нагруженной давлением
м и нагруженной давлением 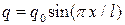 на длине
на длине 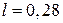 м, отношение максимального прогиба, вычисленного с учетом сдвига, к прогибу, вычисленному без учета сдвига,
м, отношение максимального прогиба, вычисленного с учетом сдвига, к прогибу, вычисленному без учета сдвига, 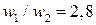 . А отношение
. А отношение 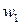 к прогибу
к прогибу 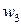 , вычисленному по более сложной методике, основанной на гипотезе ломаной линии, равно
, вычисленному по более сложной методике, основанной на гипотезе ломаной линии, равно 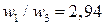 , что при заданных параметрах балки можно считать вполне удовлетворительным.
, что при заданных параметрах балки можно считать вполне удовлетворительным.