Ход урока
Сегодня на уроке речь пойдет о центре тяжести и условиях равновесия твердого тела
Центр тяжести. Условия равновесия
«Не существует тела, у которого
бы не было этой важнейшей характеристики.
Кто-то ею доволен, кто-то не очень,
но очень хочет ее изменить»
Альберт Эйнштейн
В данной теме речь пойдет о центре тяжести и условиях равновесия твердого тела.
Вспомним материал прошлых тем. Сила тяжести — это сила, с которой Земля притягивает к себе любое тело.
Рычаг – это любое твердое тело, способное поворачиваться относительно неподвижной опоры или оси. Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
В прошлых темах было получено правило моментов, согласно которому рычаг будет находиться в равновесии, если сумма моментов сил, вращающих его по ходу часовой стрелки, равна сумме моментов сил вращающих рычаг против хода часовой стрелки.
Что такое равновесие? В физике под равновесием понимают такое состояние тела, при котором воздействие на него одних сил компенсируется воздействием других сил. Иными словами, тело находится в состоянии покоя или движется равномерно и прямолинейно.
Изучение нового материала.
Каким образом можно добиться равновесия тела? Для ответа на это вопрос, возьмем какое-нибудь тело прямоугольной формы и, обвязав его петлей, подвесим на нити в произвольном месте. Как видим, тело начинает поворачиваться.
Изменим положение петли — брусок опять приходит в движение.
Однако можно найти такое положение петельки, при котором брусок будет находиться в состоянии покоя, т.е. в равновесии. Так вот, в этом случае говорят, что брусок подвешен в центре тяжести.
А что такое центр тяжести? До сих пор говорилось о силе тяжести как одной силе, действующей на тело целиком. Но на самом деле сила тяжести складывается из множества сил, приложенных к каждой части тела.

Можно ли заменить множество этих сил тяжести одной? А если можно, то в какой точке ее следует приложить?
Поставим опыт. Подвесим на нити динамометр, а к нему легкий жесткий стержень с двумя различными грузами на концах. Точку подвеса стержня подберем так, чтобы грузы уравновесили друг друга. Стержень с грузами будем рассматривать как одно тело, на которое действуют сила упругости нити и силы тяжести грузов.
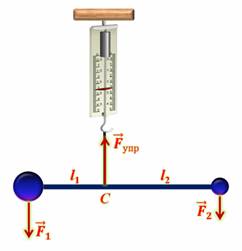
Как показывает опыт, для того, чтобы сила тяжести всего тела заменила силы тяжести грузов, ее нужно приложить в точке, относительно которой грузы уравновешивают друг друга, — т.е. в точке подвеса стержня. Только в этом случае не изменятся ни показания динамометра, ни положение стержня. Точку приложения равнодействующей сил тяжести, действующих на отдельные части тела называют центром тяжести тела.
Как можно найти центр тяжести в различных телах?
Если тело однородно и имеет правильную форму, то все просто. У однородных тел правильной формы центр тяжести совпадает с его геометрическим центром. Так, например, центр тяжести шара лежит в его геометрическом центре, у прямоугольного параллелепипеда — в точке пересечения диагоналей, а у треугольника — на пересечении его медиан.
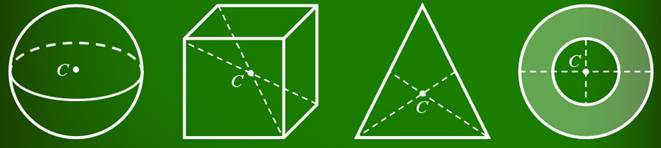
В некоторых случаях центр тяжести может находиться и вне тела. Например, у кольца он лежит на пересечении его диаметров.
А если тело имеет неправильную форму?
Поставим опыт. Возьмем пластину неправильной формы и, по ее периметру, проделаем несколько одинаковых отверстий. Теперь подвесим пластину за одно из них. Если качать пластину, то она, после нескольких колебаний, всегда будет останавливаться в одном и том же равновесном положении. Чтобы запомнить это положение, прикрепим к оси отвес и проведем вдоль него прямую линию. Теперь подвесим пластину за другое отверстие и повторим все действия с отвесом. При этом все три отвеса проходят через одну точку — это точка и будет являться центром тяжести пластины.

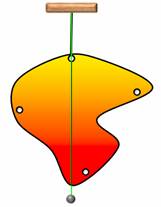
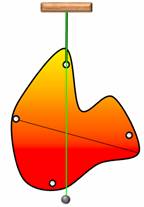
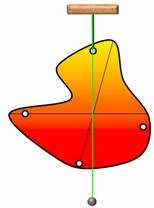
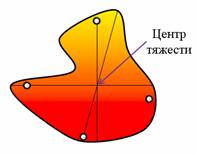
За какую бы точку не подвешивали пластину, ее центр тяжести оказывается в наинизшем положении на отвесе.
Что будет, если подвесить пластину за сам центр тяжести? В этом случае, пластина может висеть в покое или вращаться.
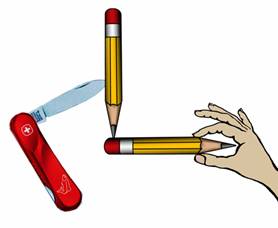
Известно, что карандаш невозможно поставить на острие, так как опорная площадка слишком мала. Однако, зная понятие центра тяжести, это можно сделать без труда. Как? Возьмем перочинный ножик, воткнем его в карандаш и поставим карандаш острием на резинку. В данном случае карандаш не падает и его даже можно слегка раскачивать. А дело все в том, что центр тяжести такой конструкции находится под опорной площадкой.
Примером устойчивого равновесия является любое тело, подвешенное на нити. Это, например, бабочки, висящие на люстре и сама люстра, лимон, висящий на лимонном дереве, маятник часов. В положении устойчивого равновесия находятся и, так называемые, висящие камни. Вот что про них пишет Александр Степанович Грин в своем произведении «Качающаяся скала»: Надо сказать, что в этих местах не редкость встретить так называемую «качающуюся скалу» — весьма любопытное явление, суть которого в том, что отдельный огромный кусок скалы в незапамятные времена получает устойчивость равновесия. Он обыкновенно стоит на каменной площадке, узким концом вниз, и, если его раскачивать, он, подобно ваньке-встаньке, принимает первоначальное положение. Такие скалы весят иногда тысячи тонн, но послушны движению руки человека средней силы. Такая скала упасть не может, если, конечно, ее не взорвут динамитом.

Примерами безразличного равновесия могут служить колеса автомобиля или мотоцикла — у них ось вращения проходит через их центр тяжести.
Об устойчивости положения тела можно судить и о величине угла поворота, необходимого для приведения тела в состояние неустойчивого равновесия. Для примера рассмотрим наклонную плоскость с невысокой ступенькой и два кубика. Выясним, при каком значении угла наклона произойдет опрокидывание кубика. Однородный кубик опрокинется при угле в 45 градусов.
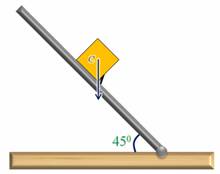
Теперь возьмем кубик, склеенный из двух половинок — деревянной и стальной. Если поставить его деревянной частью книзу, то кубик опрокинется при значительно меньшем значении угла. Если же внизу будет стальная его часть, то опрокидывание произойдет лишь при угле больше 60 градусов.
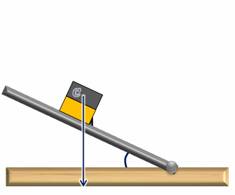
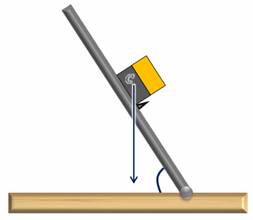
Из этого опыта можно сделать вывод, что чем больше угол, на который нужно повернуть тело, для того, чтобы оно заняло положение неустойчивого равновесия, тем устойчивее его первоначальное положение. Величина угла поворота зависит от площади опоры тела и от положения его центра тяжести.
Изучая движение тел под действием различных сил, мы пока не обращали внимание на то, что тела имеют размеры, мы считали их материальными точками. Такое упрощение верно, если все точки тела перемещаются одинаково, т.е. если тело движется поступательно. Надо выяснить к какой точке тела должна быть приложена сила для того, чтобы его движение было действительно поступательным.
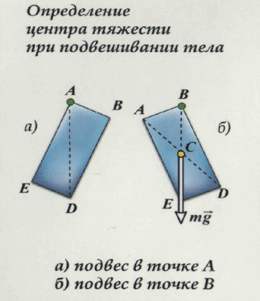
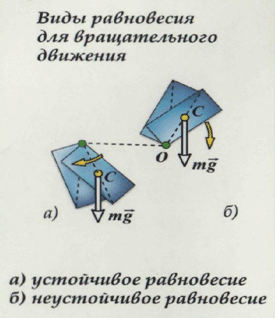
Рисунок 1 Рисунок 2
Зачем нам нужно знать положение центра масс? Если тело движется поступательно под действием одной или нескольких сил, что эта сила или равнодействующая всех сил проходит через центр масс тела. Центр масс тела в этом случае движется так, как будто в нем сосредоточена вся масса тела и к нему приложены все силы, действующие на него. Поэтому, когда мы видим, что тело движется поступательно, то это значит, что равнодействующая всех сил, приложенных к телу, проходит через его центр масс. Центр масс часто называют и центром тяжести тел.
Центром тяжести называют точку приложения равнодействующей сил тяжести, действующих на отдельные части тела.
Для того, чтобы найти центр тяжести, надо подвесить фигуру несколько раз (2–З раза), прикрепляя нитку подвес сначала в одной, а затем в другой точке тела. Точка пересечения нитей-подвесов и будет являться искомым центром тяжести.
От положения центра тяжести зависит условие равновесия тела. Равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается, называют устойчивым.
Равновесие, при котором выведенное из положения равновесия тело не возвращается в начальное положение, называют неустойчивым.
РАВНОВЕСИЕ ТЕЛ.
О ВАНЬКЕ-ВСТАНЬКЕ, ЦЕНТРЕ ТЯЖЕСТИ И РАВНОВЕСИИ
Если тело в покое, значит оно находится в состоянии равновесия. Тогда геометрическая сумма сил, а также сумма моментов, действующих на тело, равны нулю.
Большинство тел покоится на опорах, в том числе и человек. Стоящий предмет (тело на опоре), не опрокидывается, если вертикаль, проведенная через центр тяжести, пересекает площадь опоры тела.
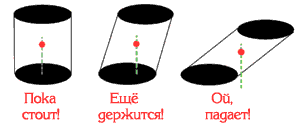
Падающая башня в итальянском городе Пиза не падает, несмотря на свой наклон, т.к. отвесная линия, проведенная из центра тяжести, не выходит за пределы основания.
Предел устойчивости тела, стоящего на наклонной плоскости удобно оценивать углом наклона. Предельный угол наклона можно определить геометрически: tag альфа = L / 2h
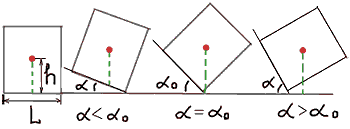
Чем больше L, тем ниже располагается центр тяжести тела (т.е. меньше h), и тем устойчивей тело на опоре.
Существуют три вида равновесия: