Изгибные колебания прямолинейных стержней.

Основные опущения:
Масса единицы длины переменная, зависит от z (как и жесткость).
Внешняя нагрузка только поперечная.
Будем определять координаты, колебания сечений.
Предполагаем, что колебания малые, т.е.  (прогибы много меньше длины). Малые перемещения, малые углы поворота.
(прогибы много меньше длины). Малые перемещения, малые углы поворота.
Есть перемещение и в продольном направлении  . Но, если колебания малые, то
. Но, если колебания малые, то  - более высокого порядка малости чем
- более высокого порядка малости чем  , то есть
, то есть  .
.
Будем использовать гипотезу плоских сечений, пренебрегая сдвиговыми деформациями.
Есть инерции движения и в продольном, и в поперечном направлении, но инерция « » б.м. более высокого порядка малости, чем «
» б.м. более высокого порядка малости, чем « ». В данной постановке задачи инерцией поворота пренебрегаем (для длинных стержней). Инерция только в вертикальном направлении.
». В данной постановке задачи инерцией поворота пренебрегаем (для длинных стержней). Инерция только в вертикальном направлении.
Таким образом, пренебрегаем сдвиговыми перемещениями и инерцией поворота.
Далее рассмотрим решение задачи методом кинетостатики.
Считаем, что 
Усилия, внутренние силовые факторы:

 (когда
(когда  не зависит от времени
не зависит от времени 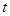 )
)
Заменяем полную производную частной:
 (тут есть некоторые допущения).
(тут есть некоторые допущения).
Силы инерции направлены только вертикально.
Рассмотрим уравнения динамического равновесия:
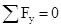
 ;
;

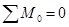
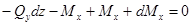 ;
;
 .
.
Замена  на
на  корректна: рассматриваем равновесие в фиксированный момент времени.
корректна: рассматриваем равновесие в фиксированный момент времени.
 , здесь
, здесь  - изменение кривизны.
- изменение кривизны.
Итак, имеем замкнутую систему уравнений относительно 4х неизвестных:  .
.
Откуда получим:
 ,
, 
Уравнение изгибных колебаний:
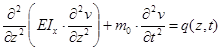 .
.
Уравнение движения в частных производных.
Для решения зададим 4 краевых условия и 2 начальных условия.
Два краевых условия на одном конце стержня, два краевых условия на другом.
Начальные условия:  ,
,  ,
,
 .
.
Рассмотрим частные случаи.
Начнем со свободных (собственных) колебаний.
Свободные (собственные) колебания


ОДУ в частных производных

Метод Фурье:
 ,
,


(Выражение равно п 
 остоянной, так как слева все зависит от координаты
остоянной, так как слева все зависит от координаты  , а справа – от времени
, а справа – от времени 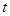 ).
).
Здесь  - частота свободных колебаний,
- частота свободных колебаний,
 ;
;
 ;
;
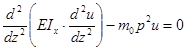 .
.
В общем случае это уравнение с переменными коэффициентами.
Предполагаем, что  ,
,  .
.
 ,
, 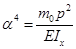 .
.
Найдем решение ДУ с постоянными коэффициентами.
 ,
,  ,
,


Решения можно скомбинировать не только через экспоненты, но и через тригонометрические и гиперболические функции.
 ,
,  ;
;
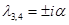 ,
, 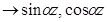 .
.
Через функции Крылова:
 ;
;
 ,
,  ,
,
 ,
, 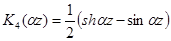 ;
;
 ,
,  ,
,  ,
, 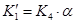
 ,
,  ;
;
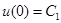 ;
; 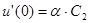 , т.е.
, т.е.  ;
;
 ;
;  .
.
Учёт граничных условий
Рассмотрим частные варианты постановки граничных условий:
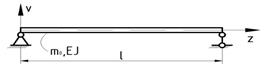 1)
1)  ,
,  ;
;
2)  ,
,  ,
, 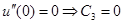 ;
;
3) 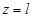 ,
,  ,
, 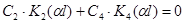 ;
;
4) 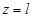 ,
,  ,
,  .
.
Получили систему линейных уравнений относительно констант C2, C4, нас интересует нетривиальное решение. Условие его существования заключается в равенстве нулю определителя:

 .
.
Это уравнение называется частотным. Из него можно найти 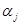 . Уравнение трансцендентное, имеем бесконечное множество корней с соответствующими частотами:
. Уравнение трансцендентное, имеем бесконечное множество корней с соответствующими частотами:


 (ноль только при αl = 0)
(ноль только при αl = 0)
Тогда:

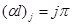 , где
, где 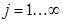 .
.
Тогда 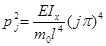
Нахождение собственных форм
Воспользуемся любым из двух нетривиальных уравнений, описывающих граничные условия:

Найдем соотношения между коэффициентами:
 - соответствует
- соответствует  -ой собственной форме
-ой собственной форме
 -
-  -я координатная функция.
-я координатная функция.
Собственная форма определяется с точностью до множителя.
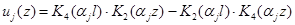
Эта координатная функция будет давать форму колебаний.
Подставим функции Крылова:
 (т.к.
(т.к. 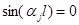 )
)
 с точностью до множителя.
с точностью до множителя.
 Покажем собственные формы колебаний:
Покажем собственные формы колебаний:



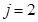 Выполняется теорема об узлах собственных форм
Выполняется теорема об узлах собственных форм


Собственных частот и колебаний  много,
много,  .
.
Полное решение этой задачи:

Постоянные  определяются из заданных начальных условий.
определяются из заданных начальных условий.
Этот ряд хорошо сходится, можно получить решение, достаточно близкое к точному.
Н.у.: 



Находим  так же, как и в продольных колебаниях.
так же, как и в продольных колебаниях.