Решение
1. Определим осевой момент инерции относительно оси Ох. Используем формулы для главных центральных моментов. Представим момент инерции сечения как разность моментов инерции круга и прямоугольника.
Для круга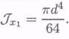 
Для прямоугольника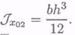 
Для прямоугольника ось Ох не проходит через ЦТ. Момент инерции прямоугольника относительно оси Ох:
где А — площадь сечения; а — расстояние между осями Ох и Охо.
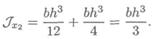
Момент инерции сечения
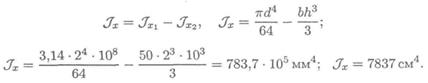
2. Осевой момент инерции относительно оси Оу:
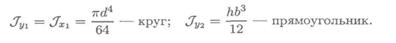
Момент инерции сечения
Задача для самостоятельного решения:
1.Определить статический момент полукруга радиусом R (рис. 4.3) относительно горизонтальной оси z, совпадающей с диаметром, и координату центра тяжести yc.
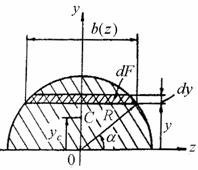
Рис.4.3
Краткие теоретические и справочно-информационные материалы по теме:
При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечением одинаково. Здесь геометрической характеристикой сечения является площадь.
При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометрические характеристики сечения, влияющие на сопротивления сечения деформированию.
Статический момент площади сечения
Рассмотрим произвольное сечение.
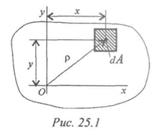
Если разбить сечение на бесконечно малые площадки аА и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выражение, получим статический момент площади сечения:
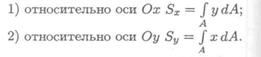
Для симметричного сечения статические моменты каждой половины площади равны по величине и имеют разный знак. Следовательно, статический момент относительно оси симметрии равен нулю.
Статический момент используется при определении положения центра тяжести сечения:
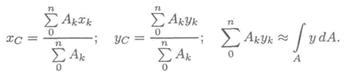
Формулы для определения положения центра тяжести можно записать в виде
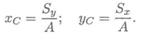
Центробежным моментом инерции сечения называется взятая по всей площади сумма произведений элементарных площадок на обе координаты:
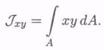
Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент инерции относительно осей, проходящих через центр тяжести сечения, равен нулю.
Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяжести, называют главными центральными осями сечения.
Осевые моменты инерции
Осевым моментом инерции сечения относительно некоторой оси, лежащей в этой же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой оси: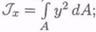 
1) осевой момент инерции сечения относительно оси Ох
21 осевой момент инерции сечения относительно оси Оу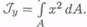 
Полярный момент инерции сечения
Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по вс^й площади сумма произведений элементарных площадок на квадрат их расстояния до этой точки:
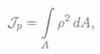
где р — расстояние до полюса (центра поворота) (рис. 25.1).
Поскольку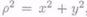 
, получим: полярный момент инерции
сечения равен сумме осевых:
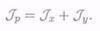
Осевые моменты инерции характеризуют сопротивление сечения повороту относительно соответствующей оси.
Полярный момент инерция характеризует сопротивление сечения повороту вокруг полюса (начала координат). Единицы измерения моментов инерции: м4; см4; мм4.