Для использования на этапе расчета фильтра графиков и таблиц, помещенных в справочниках, то есть для обращения к «каталогу фильтров», необходимо проектируемый фильтр привести к каноническое виду. Это приведение основано на двух процедурах: нормировании параметров фильтра и частотного диапазона и преобразовании частоты.
Нормирование заключается в переходе от размерных физических величин к безразмерным и близким к 1 за счет выбора подходящих нормирующих величин.
Преобразование частоты представляет собой процедуру, с помощью которой требования к ФВЧ, ПФ, ЗФ преобразуются в требования к ФНЧ, называемому «фильтром-прототипом». Эта же процедура после расчета фильтра-прототипа дает простой способ перехода от ФНЧ к более сложным типам фильтров [4], [5].
При выборе нормирующих величин следует учитывать, что полное сопротивление, частота, индуктивность и емкость связаны между собой. Поэтому только две переменные могут быть нормированы независимо. Чаще всего - это полное сопротивление и частота. Если взять нормирующую частоту f 0 в Гц и нормирующее сопротивление R0 в Ом, то получим прочие нормирующие величины:
- нормирующую емкость 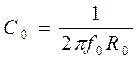 в Ф;
в Ф;
- нормирующую индуктивность  в Гн.
в Гн.
Тогда нормированные (безразмерные) значения определятся следующими выражениями:
- для частоты 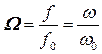 ,
,
-для сопротивления 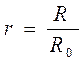 ,
,
для индуктивности 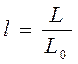 ,
,
для емкости  .
.
В качестве основных нормирующих величин R0 и w0 обычно выбираются сопротивления нагрузки R 2 (или внутреннее сопротивление источника R1) и частота в некоторой удобной точке (чаще всего частота среза wc).
Сущность преобразования частоты заключается в замене частотной переменной wнч во всех частотных характеристиках фильтра-прототипа на функцию wнч = W(w).
Такое преобразование приводит к замене индуктивного и емкостного сопротивлений прототипа на новые реактивные сопротивления, характер и величина которых могут быть определены из выражений
wнч Lнч = W(w)Lнч
1/wнч Снч=1/W(w) (8)
Подробные сведения об этих преобразованиях содержатся в [4], [5], [8]. Ниже приведены только правила преобразования элементов и расчетные соотношения для основных видов преобразований.
Преобразование ФНЧ-ФНЧ (масштабирование по частоте). Осуществляется путем следующей замены переменной:
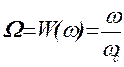 (9)
(9)
Таким образом, если фильтр-прототип имел частоту среза, равную 1, то новый фильтр будет иметь частоту среза wс.
Характер реактивных сопротивлений в преобразованной схеме сохраняется, изменяется только величина элементов:
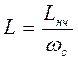 ,
, 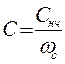 (10)
(10)
Преобразование ФНЧ – ФВЧ
Осуществляется путем следующей смены переменной:
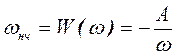 , (11)
, (11)
При этом индуктивное сопротивление прототипа wнчLнч преобразуется в емкостное
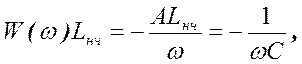 (12)
(12)
где  ,
,
и наоборот емкостное - в индуктивное
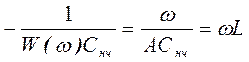 , (13)
, (13)
где 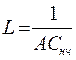 .
.
Преобразование частоты в соответствии с (11) приводит к тому, что точки на АЧХ фильтра-прототипа, соответствующие частоте среза wснч и границе полосы подавления (частоте гарантированного затухания) wsнч, отображаются в точка, соответствующие частоте среза и частоте гарантированного затухания ФВЧ:
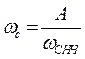 ;
; 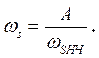 (14)
(14)
В частности, если преобразованию подвергается нормированный фильтр-прототип с частотой среза Wcнч = 1, то параметр преобразования А равен частоте среза проектируемого ФВЧ.
При задании требований к характеристике затухания ФВЧ необходимая избирательность фильтра-прототипа, определяющая его порядок, вычисляется из соотношения
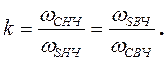 (15)
(15)
Преобразование ФНЧ в ПФ.
Функция преобразования имеет следующий вид:
 , (16)
, (16)
где w0 является требуемой средней частотой, а параметр В определяется полосой пропускания ПФ.
Преобразование частоты в соответствии с (16) обладает следующими свойствами:
1. Точка на характеристике ФНЧ, соответствующая wнч=0, отображается на две средние частоты w0 и - w0. Точка, лежащая в бесконечности, отображается на начало координат.
2. В общем случае любая точка на характеристике ФНЧ, соответствующая частоте wнч, отображается на две точки, соответствующие частотам, являющимися корнями квадратного уравнения
w2 - Bwнч w - w02 = 0 (17)
В частности, граница полосы пропускания wснч и полосы подавления wsнч преобразуются в две точки каждая (wс1 и -wс2, ws1 и -ws2), что подтверждает получение характеристики, соответствующей полосовому фильтру.
3. Границы полос пропускания и полос подавления относительно центральной частоты w0 расположены с соблюдением не арифметической, а геометрической симметрии:
wc1 wc2 = w02, ws1 ws2 = w02. (18)
4. Сумма частот, в которые преобразуется любая частотная точка прототипа, постоянна. В частности,
wc1 - wc2 = Bwcнч, ws1 - ws2 = Bwsнч. (19)
Из (19) можно определить параметр избирательности фильтра-прототипа, если заданы требования к АЧХ ПФ:
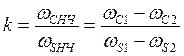 (20)
(20)
При таком преобразовании индуктивное сопротивление в схеме прототипа в ПФ заменяется сопротивлением последовательного LC -контура:
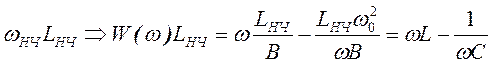 , (21)
, (21)
где L=Lнч / B, C=B/(Lнчw02).
Соответственно емкостное сопротивление преобразуется в сопротивление параллельного LC - контура:
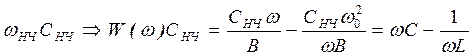 , (22)
, (22)
где С=Снч/B, а L=B/(w02 Cнч).
5. Расчет и реализация пассивных LC – фильтров
Под пассивным фильтром далее подразумевается реактивный четырехполюсник (четырехполюсник без потерь), нагруженный со стороны выходных зажимов на сопротивление нагрузки R2, а со стороны входных - на внутреннее сопротивление генератора R1, как это показано на рис. 2. 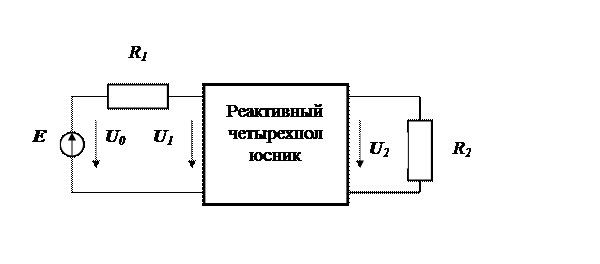 Рис. 2. Реактивный четырехполюсник с нагрузкой на входе и выходе
Рис. 2. Реактивный четырехполюсник с нагрузкой на входе и выходе
При расчете таких фильтров для их описания вводят два коэффициента - коэффициент передачи мощности и коэффициент отражения, определяемые по следующей методике [4], [5].
Максимальная мощность, которая может поступить от источника в нагрузку, равна
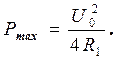 (23)
(23)
Мощность, поступающая в нагрузку через реактивный четырехполюсник, определяется выражением
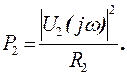 (24)
(24)
С учетом (23) и (24) коэффициент передачи мощности определяется отношением
 (25)
(25)
Коэффициент отражения определяется как дополнение коэффициента передачи мощности до 1:
 (26)
(26)
Отсюда следует, что изменение коэффициента отражения в полосе пропускания приводит к изменению затухания на величину
 , дБ (27)
, дБ (27)
Иначе
 (28)
(28)
В справочниках по расчету фильтров [7], [9] используют как максимально допустимый коэффициент отражения, так и максимальную неравномерность АЧХ затухания.
Часто вместо коэффициента передачи мощности используется характеристическая функция J (jw), определяемая из соотношения
 (29)
(29)
откуда следует, что
 (30)
(30)
Существует несколько методов реализации заданной передаточной функции пассивной цепью. Наибольшее распространение получили три основные схемные структуры: лестничные схемы, мостовые схемы и схемы Дарлингтона [2], [4], [6]. Тематика курсовой работы предполагает разработку пассивного LC -фильтра лестничной структуры, пример такой схемы приведен в Приложении 1 на рис. 6. Лестничные схемы обладают важным преимуществом, вытекающим из следующего свойства: нуль передачи лестничной цепи достигается на тех частотах, на которых полное сопротивление последовательной ветви или полная проводимость параллельной ветви равны бесконечности. Из этого следует, что каждой ветвью обусловлен нуль передачи (полюс затухания). Это делает настройку лестничного фильтра относительно простой. Также благодаря этому нули передачи (полюса затухания) менее чувствительны к изменению параметров элементов, по сравнению со схемами, в которых частота полюса (нуля) определяется условием баланса моста [5].
Расчет пассивного LC -фильтра лестничной структуры осуществляется в следующей последовательности.
1. Нормирование частоты и определение нормирующих параметров элементов фильтра.
2. Переход к фильтру-прототипу и определение параметра избирательности фильтра-прототипа.
3. Выбор типа и порядка фильтра-прототипа.
4. Определение по таблицам и графикам нормированных параметров фильтра-прототипа.
5. Преобразование частоты - переход от фильтра-прототипа к ФВЧ или ПФ.
6. Денормирование параметров элементов фильтра.
Нормирование частоты можно производить и после перехода к фильтру-прототипу.
6. Реализация фильтров с помощью активных RC -цепей
Реализация активных RC -фильтров осуществляется с использованием одного или нескольких активных приборов: транзисторов, зависимых источников и т.п. Наиболее часто применяемым активным прибором является операционный усилитель (ОУ), выполненный в виде интегральной схемы. ОУ представляет собой устройство с двумя входами (инвертирующим и неинвертирующим) и одним выходом, которое обладает большим коэффициентом усиления К0, постоянным в широком диапазоне частот, начиная с нулевой. У идеального ОУ входные сопротивления равны бесконечности, а выходное сопротивление равно нулю. Выходное напряжение ОУ равно
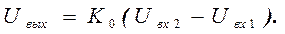 (31)
(31)
Условное обозначение и эквивалентная схема ОУ приведены на рис 3.
 |
 |
Рис. 3. Условное обозначение и эквивалентная схема идеального ОУ
Реализация активных RC -фильтров может осуществляться в прямой или каскадной форме. В первом случае заданная передаточная функция реализуется непосредственно как передаточная функция одного фильтра. Во втором случае используется каскадное соединение звеньев, состоящих из активных фильтров второго порядка и активных или пассивных фильтров первого порядка с соответствующей развязкой между каскадами. Такая реализация позволяет проводить независимую подстройку каждого звена фильтра. Каскадные структуры, как правило, менее чувствительны к изменениям параметров элементов, чем фильтры прямой структуры.
Из выражения.(6) следует, что передаточная функция фильтра первого порядка имеет вид
 (32)
(32)
где M(p) -полиномом первой или нулевой степени.
Для фильтров второго порядка передаточная функция
 (33)
(33)
В частности, для фильтров Баттерворта и Чебышева нижних частот числитель равен а0, для ФВЧ - p2, а для ПФ – a1p.
Каскадная реализация фильтра четного порядка n содержит n/2 звеньев второго порядка, каждое с передаточной функцией типа (33). Для фильтра нечетного порядка схема содержит (n-1)/2 звеньев второго порядка и одно звено первого порядка с передаточной функцией типа (32).
Таким образом, основная задача проектирования состоит в реализации передаточной функции второго порядка (33). При этом дополнительно необходимо обеспечить большое входное и малое выходное сопротивление каскада, чтобы избежать применения дополнительных развязывающих каскадов.
Удобным описанием передаточной функции второго порядка является система обобщенных параметров: добротность полюса (нуля)
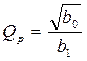 ,
, 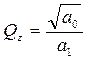 (34)
(34)
и собственная частота полюса (нуля)
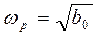 ,
, 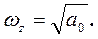 (35)
(35)
Передаточная функция фильтра второго порядка через эти параметры определяется следующим образом:
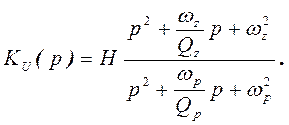 (36)
(36)
Применение справочников и таблиц для расчета фильтров предполагает использование нормированных значений частот полюса и нуля. Если нормирование осуществляется относительно частоты среза, т.е. Wp=wp/wВ и Wz=wz/wВ, то выражение (36) приобретает вид
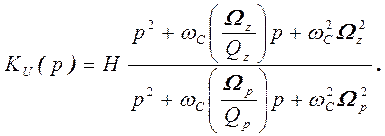 . (37)
. (37)
Выражение для передаточной функции в форме (37) является основным при расчете фильтров второго порядка.
Рассмотрим общие принципы реализации передаточной функции вида (37) с помощью ОУ, охваченного обратной связью. Пассивная часть схемы представляет собой многополюсник состоящий из резистивных и емкостных элементов (рис. 4).
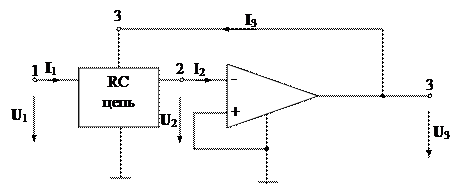 |
Рис. 4. Фильтр на базе ОУ с обратной связью.
Чтобы получать выражение для передаточной функция, составим уравнения, описывающие пассивную часть схемы, используя метод узловых напряжений и матрицу узловых проводимостей:

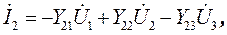 (38)
(38)
 .
.
Полагая, что в идеальном ОУ входная цепь не потребляет тока (т.е. I 2 = 0), и учитывая, что U 2= - U 3/K0, из второго уравнения (38) получаем
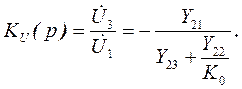 (39)
(39)
Из этого выражения следует, что при большом коэффициенте усиления ОУ передаточная функция активного фильтра определяется только параметрами RC-цепи:
 . (40)
. (40)
Одной из наиболее простых схем, реализующих изложенный выше принцип построения активных фильтров, является схема с многопетлевой обратной связью (рис. 5).
 |
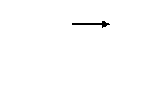
Рис. 5. Активный фильтр с многопетлевой обратной связью.
Составив уравнения по методу узловых напряжений и положив, как и ранее, что входной ток ОУ равен нулю, а выходное напряжение
U 3= -K0 U 2,
после несложных преобразований приходим к следующему выражению для передаточной функции этой схемы:
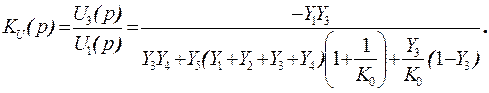 (41)
(41)
При K0®¥ это соотношение принимает вид
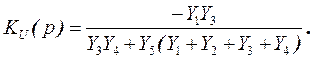 . (42)
. (42)
Реализация нужной передаточной функции звена второго порядка сводится, таким образом, к подбору проводимостей элементов, которые могут быть либо резисторами с проводимостью 1/R, либо конденсаторами, с проводимостью, равной pC. В частности из (42) следует, что для реализации ФНЧ необходимо, чтобы проводимости Y1, Y3 и Y4 были резистивными, а Y2, Y5 - емкостными.
Другие способы реализации звена второго порядка отличаются структурой RC -цепи и включением ОУ. Так широко применяются схемы с однопетлевой обратной связью и неинвертирующим включением ОУ (фильтры на источнике напряжения, управляемым напряжением - ИНУН), схемы, использующие несколько ОУ (биквадратные фильтры, фильтры на трех конденсаторах и др). Со способами реализации этих фильтров можно ознакомиться в монографиях и справочниках [3],[4],[8]. Отметим, что, как правило, передаточные функции второго порядка при малых в средних значениях добротности (менее 20) реализуются с помощью относительно простых схем. При высоких значениях добротности (свыше 20) требуются более сложные схемы [10].
7. Порядок расчета активных RC -фильтров
Активные RC -фильтры нижних частот рассчитываются в следующем порядке.
1. Определяется нормированное значение частоты гарантированного затухания (или переходной полосы). По заданным величинам гарантированного затухания и неравномерности АЧХ в полосе пропускания с использованием свойств АЧХ фильтра соответствующего типа находится минимальный порядок фильтра.
2. Передаточная функция фильтра n -го порядка представляется в виде произведения функций звеньев второю порядка, общий вид которых определяется выражениями (33) и (37). При этом для фильтров Баттерворта и Чебышева передаточная функция звена второго порядка приводится к виду:
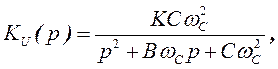 (43)
(43)
а для инверсных Чебышева и эллиптических фильтров эта функция принимает вид:
 (44)
(44)
Для фильтров нечетных порядков к передаточной функции добавляется сомножитель, соответствующий функции звена первого порядка, который для всех типов фильтров задается в виде
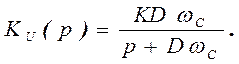 (45)
(45)
Заметим, что выражения (43) и (44) являются частным случаем выражения (37), а (45) - частным случаем (32). Во всех случаях К представляет собой коэффициент усиления звена на нулевой частоте, а коэффициенты А, В, С и D - суть коэффициенты полиномов передаточной функции соответствующих нормированных фильтров (с частотой среза, равной 1), определяемые из (32) и (37) на основе соотношений:
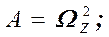
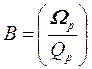 ;
; 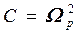 ;
; 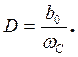 (46)
(46)
Рассчитанные для различных типов и различных порядков фильтров эти коэффициенты наиболее полно представлены в справочнике [8].
3. Выбираются схемы, реализующие передаточные функции типовых звеньев второго и первого порядков, и рассчитываются параметры этих схем. В частности, для схемы, изображенной на рис. 5, параметры проводимостей определяются на основании сопоставления выражений (42) и (43) или (44).
Методика расчета параметров различных схем типовых звеньев второго и первого порядка подробно изложена в [3], [4], [8], [10].
Расчет активных фильтров верхних частот производится в такой же последовательности. Отличие заключается только в виде выражений для передаточных функций типовых звеньев первого и второго порядков и в характере элементов, входящих в схемы, реализующих эти функции.
Поскольку передаточную функцию ФВЧ с частотой среза wсвч можно получить из передаточной функции нормированного ФНЧ (с частотой среза, равной 1 рад/с) путем замены переменной р на wсвч/p, то из (42), (43) и (44) следует, что функция ФВЧ Баттерворта и Чебышева второго порядка описывается выражением
 (47)
(47)
Функция ФВЧ инверсного Чебышева и эллиптического второго порядка имеет вид
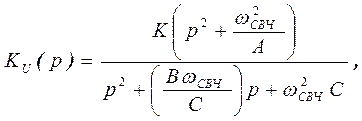 (48)
(48)
а в передаточные функции фильтров нечетного порядка в качестве сомножителя входит функция звена первого порядка вида
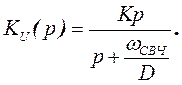 . (49)
. (49)
В уравнениях (47), (48) и (45) К является коэффициентом усиления звена, а параметры А, В, С и D – коэффициенты соответствующих передаточных функций нормированных ФНЧ, рассчитываемые по выражениям (46).
Содержание и оформление пояснительной записки
Общие требования к правилам оформления пояснительных записок изложены в методических указания [14], [15]. В соответствии с этими требованиями рекомендуется следующая последовательность размещения материала:
- титульный лист;
- реферат;
- содержание;
- перечень условных обозначений, единиц, символов и терминов;
- введение (включающее общую постановку задачи и конкретное задание на проектирование);
- основная часть, в которой описываются свойства и характеристики проектируемого фильтра, производится расчет фильтра, выбор, обоснование и описание схемы, выражения для АЧХ и ФЧХ, описание методики расчетов на ПЭВМ, результаты анализа фильтра с использованием ПЭВМ и их оценка (основная часть может делиться на разделы, пункты и подпункты);
- заключение, содержащее основные выводы по работе,
- список использованных источников,
- приложения.
Пояснительная записка должна быть написана на листах белой бумаги формата А4 (210х297 мм). На листах пояснительной записки делаются рамка и основная надпись (штамп). В пояснительной записке в курсовой работе допускается основную надпись не делать. Иллюстрации (рисунки и графики) выполняются с указанием масштабов и помещаются на листах формата А4 с включением в общую нумерацию страниц после первой ссылки на них в тексте. Распечатки результатов расчетов на ПЭВМ должны соответствовать формату А4 и помещаются в приложении.