Законы Ома и Кирхгофа в операторной форме

 

Первый закон Кирхгофа

.

Второй закон Кирхгофа

.

Правило составления операторных уравнений по I и II законам Кирхгофа точно такое, как для действительных токов.

Для k -ой ветви, содержащей элементы , имеем:

.

Согласно (8-10), операторное уравнение при ненулевых начальных условиях имеет вид

или

.

Величину

(11)

называют обобщенным, или операторным сопротивлением ветви.

Операторная запись законов Кирхгофа

.

Закон Ома для k -й ветви

.

Следует отметить, что структура записи операторного сопротивления ветви и комплексное сопротивление той же ветви тождественны. Одно из другого можно получить заменой 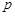на , т.е. .

При нулевых начальных условиях способ расчета любых сложных цепей при переходных процессах операторным методом аналогичен способам расчета установившихся процессов комплексным методом.

При ненулевых начальных условиях II закон Кирхгофа можно записать

.

Рассматривая члены и как ЭДС добавочных источников энергии в контурах, можно использовать все общие методы расчета сложных цепей.

При расчете токов переходных процессов в сложных цепях операторным методом необходимо составить для данной цепи эквивалентную операторную схему замещения. В этом случае необходимо знать операторные схемы замещения отдельных схемных элементов (рис. 6).

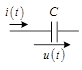
Рис.6. Соответствие изображений с ненулевыми начальными условиями
во временной и операторной областях

В частности, можно воспользоваться методом наложения и рассчитать процесс в цепи сначала при нулевых начальных условиях, а затем наложить на него процесс, возникающий только под действием одних добавочных ЭДС, т.е. обусловленный первоначальным запасом энергии в цепи.

Рассмотрим, как можно преобразовать операторные схемы при последовательном и параллельном соединениях нескольких участков.

Пусть цепь состоит из одного контура:

.

Величина является операторным сопротивлением всей цепи. При последовательном соединении участков их операторные сопротивления складываются.

Рассмотрим параллельное соединение двух ветвей, в каждой из которых имеются элементы :

где .

Суммарный ток в неразветвленной части цепи

.

Очевидно, что при ненулевых начальных условиях нельзя представить как произведение на некоторый множитель , имеющий смысл операторной проводимости. Это можно записать только при нулевых начальных условиях:

.

Величина

,

называется операторной проводимостью.

 

3.3.Переход от изображения к оригиналу. Теорема разложения

 

Функции токов и напряжений, преобразованные по Лапласу могут быть представлены, как отношение полиномов

(12)

где , полиномы от 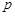, причем и коэффициенты и действительные. Изложим содержание второй теоремы разложения, позволяющей находить оригинал по изображению (12).

Если известны корни многочлена то зависимость (12) можно переписать в виде

где — кратность корня , – количество различных корней.

1. Пусть

где – различные вещественные и комплексные корни.

Тогда оригинал находят по формуле

2. Если изображение имеет вид

т.е. один характеристический корень равен нулю, то

или

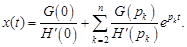
Нулевой корень появляется когда в цепи имеются источники постоянной ЭДС. Выделенный постоянный член представляет собой установившийся ток или напряжение в цепи.

3. Случай кратных корней.

Пусть

где

Тогда оригинал находят по формуле

.

Коэффициенты определяются зависимостью

Пример расчета цепи

Главное достоинство операторного метода для расчета переходных процессов, заключающееся в алгебраизации дифференциальных уравнений цепи, особенно проявляется при расчете сложных цепей. Учитывая члены 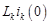u как добавочные ЭДС, можно применить к расчету переходных процессов все методы расчета сложных цепей. Решим задачу, рассмотренную в пункте 2.2, операторным методом. Соответствующая схема замещения представлена на рис. 6.

Рис. 6. Схема замещения в операторной форме

Применяя к схеме замещения в операторной форме известные методы расчета цепей постоянного тока, найдем искомые токи в операторной форме. Воспользуемся методом непосредственного использования законов Кирхгофа. Имеем

Учитывая, что для данного случая , , получим

или в матричном виде

Отсюда находим

, (13)

, (14)

. (15)

Теперь можно найти оригиналы изображений (13-15). Для этого представим изображения в следующем виде:

, , .

где , , ,

. (16)

Тогда согласно второй теореме разложения имеем

где , – корни многочлена (16).

В результате получаем

,

,

.

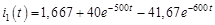Как видно, найденные токи полностью совпадают с токами, рассчитанными классическим методом.

 

4. домашнее задание

Варианты заданий

На приведены схемы электрических цепей, у которых переходные процессы вызываются замыканием (или размыканием) ключа « ». Коммутация происходит в момент времени . В цепи действует источник постоянной ЭДС . Требуется определить токи (или напряжения) двумя методами: классическим и операторным.

В соответствии с заданиями одни студенты решают задачи вариант « », другие – варианта « ». На основании полученного аналитического выражения строится график изменения искомой величины в зависимости от времени.

Вариант 1

Определить:

А. Напряжение на катушке при переходном процессе.

В. Напряжение на конденсаторе при переходном процессе.

Вариант 2

Определить:

А. Ток в конденсаторе при переходном процессе.

В. Ток в резисторе при переходном процессе.

Вариант 3

	3,2					-

Определить:

А. Ток в конденсаторе при переходном процессе.

В. Ток в индуктивности при переходном процессе.

 

Вариант 4

						-

Определить:

А. Напряжение на индуктивности при переходном процессе.

В. Ток в резисторе при переходном процессе.

Вариант 5

Определить:

А. Напряжение на индуктивности при переходном процессе.

В. Напряжение на конденсаторе при переходном процессе.

Вариант 6

 

	0,1	2,5				-

Определить:

А. Ток в резисторах и при переходном процессе.

В. Ток в конденсаторе при переходном процессе.

Вариант 7

	0,4

Определить:

А. Ток в резисторе при переходном процессе.

В. Ток в индуктивности при переходном процессе.

Вариант 8

Определить:

А. Ток в конденсаторе при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

 

Вариант 9

Определить:

А. Ток в индуктивности при переходном процессе.

В. Ток в конденсаторе при переходном процессе.

Вариант 10

	0,4

Определить:

А. Ток в индуктивности при переходном процессе.

В. Напряжение на конденсаторе при переходном процессе.

Вариант 11

		0,1

Определить:

А. Ток в резисторе при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

Вариант 12

	0,64					-

Определить:

А. Напряжение на индуктивности при переходном процессе.

В. Ток в конденсаторе при переходном процессе.

Вариант 13

Определить:

А. Напряжение на конденсаторе при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

 

 

 

Вариант 14

Определить:

А. Ток в резисторе при переходном процессе.

В. Ток в конденсаторе при переходном процессе.

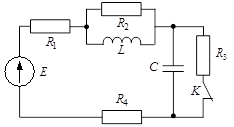
Вариант 15

Определить:

А. Ток в индуктивности при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

Вариант 16

Определить:

А. Ток в конденсаторе при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

Вариант 17

Определить:

А. Напряжение на индуктивности при переходном процессе.

B. Ток в конденсаторе при переходном процессе.

Вариант 18

Определить:

А. Ток в резисторе при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

 

Вариант 19

					-	-

Определить:

А. Ток в резисторах и при переходном процессе.

В. Напряжение на индуктивности при переходном процессе.

Вариант 20

Определить:

А. Напряжение на индуктивности при переходном процессе.

В. Напряжение на конденсаторе при переходном процессе.

 

Требования к оформлению

1. Домашнее задание выполняется на листах формата 210×297 мм.

2. Прежде чем приступить к решению задачи, необходимо под заголовком "Задание" полностью переписать задание из пособия и перечертить схему.

3. Если для выполнения домашнего задания используются математические пакеты (вычисление корней полинома, решение системы уравнений и т.д.), то необходимо в местах их непосредственного использования привести соответствующие листинги программ (или их вырезки) с комментариями.

4. При построении графиков обязательно указываются величины, отложенные вдоль осей и единицы измерения.

5. Решение задачи разными методами начинается с новой страницы, с указанием соответствующего метода озаглавленной "Решение". Вначале целесообразно построить схему и нанести на ней положительные направления токов и напряжений.

Затем составляются уравнения в общем виде. Дальнейшие расчеты рекомендуется вести не в общем виде, а подставляя конкретные числа.

6. Все расчеты целесообразно сопровождать пояснениями и проводить по пунктам в последовательности, указанной в задании.

7. В окончательных числовых результатах обязательно следует указать единицы измерения, в которых получен ответ.

8. При решении следует пользоваться обозначениями международной системы единиц СИ.

 

5. Контрольные вопросы

 

1. Дайте понятие переходного процесса в электрической цепи.

2. Сформулируйте законы коммутации.

3. В чем заключается сущность классического (операторного) метода расчета переходных процессов? Назовите их достоинства и недостатки.

4. Чем определяется порядок дифференциальных уравнений?

5. Что такое характеристическое уравнение? Что определяется из этого уравнения?

6. Что такое постоянная интегрирования? Как она определяется при расчетах переходных процессов?

7. Опишите порядок расчета переходного процесса классическим (операторным, частотным) методом.

8. Что понимают под выражениями «независимые условия начальные» и «зависимые условия начальные»?

9. Что такое свободная составляющая переходного процесса? Что такое принужденная составляющая переходного процесса?

10. Чем отличается апериодический переходный процесс от колеба-тельного в электрической цепи?

11. Объясните возникновение затухающих колебаний в электрических цепях при коммутациях с физической точки зрения.

12. Назовите правила составления комплексных (операторных) схем замещения.

13. Как можно найти изображение функции?

17. Какие способы перехода от изображения к оригиналу функции вы знаете?

18. Существует ли связь между прямым преобразованием Лапласа и прямым преобразованием Фурье?

 

Список литературы

1. Л.А. Бессонов Теоретические основы электротехники. Электрические цепи. Изд-во Юрайт, Серия: Бакалавр, 704 с. 2011 г.

2. Г.И. Атабеков. Теоретические основы электротехники. Линейные электрические цепи. Изд-во Лань, Серия: Учебники для вузов. Специальная литература, 592 с, 2010 г.

3. Макаров И.М., Менский Б.М. Таблица обратных преобразований Лапласа и обратных -преобразований: Дробно-рациональные изображения.: Учебное пособие для втузов. – М.: Высш. школа, 1978. – 247 с.

 

Содержание

1. Возникновение переходных процессов и законы коммутации 3

2. Классический метод расчета переходных процессов 6

2.1. Теоретические сведения 6

2.2. Пример расчета цепи. 9

3. Операторный метод расчета переходных процессов 14

3.1. Операторное изображение функций, их производных
и интегралов. 14

3.2. Законы Ома и Кирхгофа в операторной форме 18

3.3. Переход от изображения к оригиналу.
Теорема разложения. 21

3.4. Пример расчета цепи. 23

4. Домашнее задание 25

4.1. Варианты заданий. 25

4.2. Требования к оформлению. 33

5. Контрольные вопросы 34

Список литературы 35