Точность систем в установившемся режиме
Для определения ошибки системы в установившемся режиме 
при 
воспользуемся теоремой о предельном переходе 
при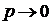 
.
Для определения установившегося значения ошибки представим передаточные функции в следующем виде: 
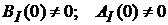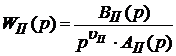, где 
;
, где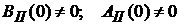 
;
uI – разность числа интегрирующих и дифференцирующих звеньев в передаточной функции 
;
uII – разность числа интегрирующих и дифференцирующих звеньев в передаточной функции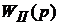 
;
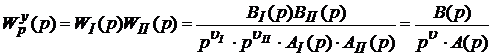, где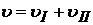 
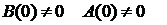
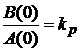
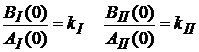
Ошибки по управляющему воздействию
.
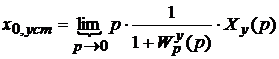
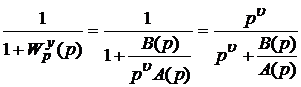Рассмотрим типовые входные воздействия и их изображения; при этом ограничимся степенными входными сигналами:
Степенные входные сигналы
| f(t) | F(p) |
| 1(t) | 1/p |
| t×1(t) | 1/p2 |
| tn/n! | 1/pn+1 |
Если уровень входного сигнала равен а, то изображение по Лапласу также умножается на а, таким образом, 
.
Если n=0, то входным сигналом является единичная ступенчатая функция 1(t) и при его отработке возникает статическая ошибка. Таким образом, статической ошибкой по какому-либо воздействию называется ошибка, возникающая при отработке этого постоянного входного воздействия.
Если n=1, то входным сигналом является линейная возрастающая функция t×1(t) и при его отработке возникает кинетическая ошибка. Таким образом, кинетической ошибкой по какому-либо воздействию называется ошибка, возникающая при отработке этого линейно возрастающего входного воздействия.
Если n=2, то входным сигналом является квадратичная функция t2×1(t) и при его отработке возникает ошибка, которая называется ошибкой по ускорению. Таким образом, ошибкой по ускорению по какому-либо воздействию называется ошибка, возникающая при отработке этого квадратичного входного воздействия.
|
|
Примем в качестве входного управляющего сигнала сигнал вида 
, для которого изображение по Лапласу имеет вид: 
. Тогда ошибку по управлению можно записать в виде: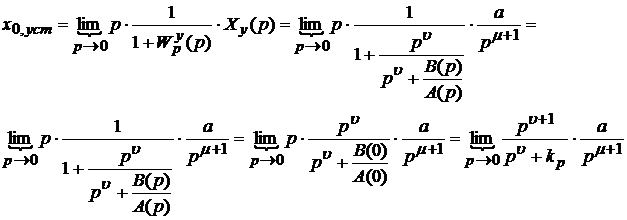 
Как видно из приведенной формулы, ошибка при отработке степенного управляющего воздействия зависит от уровня входного сигнала а, коэффициента усиления разомкнутой системы и соотношения между u и m.
Результат можно свести в таблицу:
| u m | Примечания | |||
| a/(1+kp) | Статическая ошибка по управлению | |||
| ¥ | a/kp | Кинетическая ошибка по управлению | ||
| ¥ | ¥ | a/kp | Ошибка по ускорению (по управлению) | |
| Примечания | Статическая САУ по управлению | Астатическая САУ по управлению | САУ с астатизмом 2-го порядка управлению |
Введем некоторые определения:
Статической называется САУ, отрабатывающая постоянный сигнал с конечной ошибкой.
Кинетической называется САУ, отрабатывающая линейно возрастающий сигнал с конечной ошибкой.
Системой с астатизмом 2-го порядка называется САУ, отрабатывающая линейно возрастающий сигнал с конечной ошибкой.
Системой с астатизмом u-го порядка называется САУ, отрабатывающая степенной сигнал u - го порядка с конечной ошибкой.
Конечные значения ошибок прямо пропорциональны уровню входного сигнала, обратно пропорциональны коэффициенту усиления разомкнутой системы по управлению. При соотношении u > m ошибка принимает нулевое значение, а при соотношении u < m ошибка в установившемся режиме бесконечна, т.е. система не отрабатывает входного управляющего сигнала и отклонение со временем увеличивается.
|
|
Величина u называется порядком астатизма по управлению и равна разности числа интегрирующих и дифференцирующих звеньев, лежащих в цепи обратной связи между сигналом ошибки и управляющим входным воздействием, т.е. лежащих в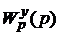 
.
Пример№1. Определение точности САУ.
Найти статическую и кинетическую ошибки по управлению и возмущению для системы, заданной структурной схемой:
Решение:
Рассчитаем ошибки системы, представленной структурной схемой:
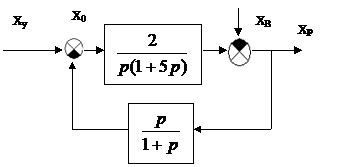
Структурная схема САУ
Для вычисления ошибки по управляющему сигналу запишем передаточную функцию ошибки по управлению:
.
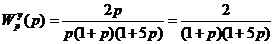Статическая ошибка по управлению:
.
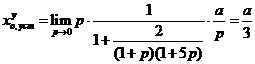Кинетическая ошибка по управлению:
.
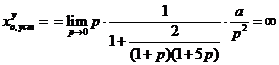Для вычисления ошибки по возмущающему сигналу запишем передаточную функцию ошибки по возмущению:
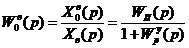, где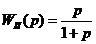 
.
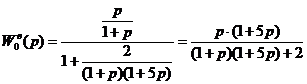Статическая ошибка по возмущению: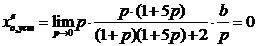 
.
Кинетическая ошибка по управлению: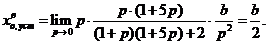 
Таким образом, система является статической по управляющему воздействию и астатической по возмущающему воздействию.
Ответ:
Статическая и кинетическая ошибки по управлению отличны от нуля и соответственно равны а/3 и бесконечности.
Статическая и кинетическая ошибки по возмущению соответственно равны 0 и b/2
Пример №2
Найти статическую и кинетическую ошибки по управлению и возмущению для системы, заданной структурной схемой:
Xв _
2) Xy + X0 + Xp
W1(p) W2(p)
_
 |
, 
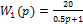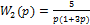
Решить самостоятельно.