6. На бесконечной ленте выписаны в порядке возрастания все натуральные числа с суммой цифр 2018. Какое число написано на 225-м месте? (Методкомиссия)
Ответ. 39…998 (223 девятки). Решение. Так как 2018 = 9×224+2, самым маленьким числом с суммой цифр 2018 будет 29…9 (224 девятки), а вторым по величине — число 389…9 (223 девятки) В 223 следующих по величине числах с суммой цифр 2018 восьмёрка «путешествует» из начала в конец ряда девяток, каждый раз смещаясь на один знак. Через 223 шага она окажется в конце числа, что и даёт нам ответ.
7. В полдень Вася положил на стол 10 вырезанных из бумаги выпуклых десятиугольников. Затем он время от времени брал ножницы, разрезал по прямой один из лежащих на столе многоугольников на два и клал оба получившихся куска назад на стол. К полуночи Вася проделал такую операцию 51 раз. Докажите, что в полночь среди лежащих на столе многоугольников был треугольник или четырёхугольник. (И. Рубанов)
Решение. Так как после каждого разрезания число многоугольников увеличивалось на 1, в полночь на столе лежал 61 многоугольник. Допустим, у каждого из этих многоугольников было не меньше пяти вершин. Тогда всего вершин у многоугольников на столе в полночь было по крайней мере 5×61 = 305. Но при каждом разрезании суммарное число вершин увеличивалось на 2 (если разрез проходил через две вершины), 3 (если разрез проходил через одну вершину и одну точку внутри стороны) или 4 (если разрез проходил через две точки внутри сторон). Поэтому общее число вершин за 51 разрезание могло увеличиться не больше, чем на 51×4 = 204, и потому суммарное число вершин в полночь не превосходило 100+204 = 304. Противоречие.
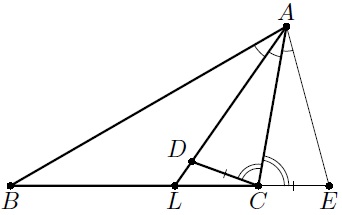8. На биссектрисе AL треугольника ABC выбрана точка D. Известно, что ÐBAC = 2a, ÐADC = 3a, ÐACB = 4a. Докажите, что BC+CD = AB. (А. Кузнецов)
Решение. На продолжении отрезка BC за точку C выберем точку E так, что CD = CE. Тогда Ð ACD = 180°–Ð DAC –Ð ADC = 180°–4a = Ð ACE. Следовательно, треугольники ACD и ACE равны по двум сторонам и углу между ними, поэтому Ð AEC = Ð ADC = 3a и Ð CAE = Ð CAD = a. Заметим, что Ð BAE = Ð BAC +Ð CAE = 3a = Ð AEB. Таким образом, треугольник ABE равнобедренный и AB = BE = BC + CE = BC + CD.
9. На клетчатой белой доске размером 25´25 клеток несколько клеток окрашено в чёрный цвет, причём в каждой строке и каждом столбце окрашено ровно 9 клеток. При каком наименьшем k заведомо можно перекрасить k клеток в белый цвет таким образом, чтобы нельзя было вырезать чёрный квадрат 2´2? (С. Берлов)
Решение. Оценка. Заметим, что если в строчке закрашено 9 клеток, то можно перекрасить четыре из них так, чтобы никакие две закрашенные клетки не были соседними: достаточно перенумеровать закрашенные клетки слева направо и перекрасить клетки с чётными номерами. Если сделать такие перекрашивания со всеми чётными строками, то перекрасится 48 клеток и не будет закрашенных квадратов 2´2, поскольку не будет двух соседних закрашенных клеток в одной чётной строке.
Пример. Закрасим расположенные вдоль главной диагонали непересекающиеся квадраты: первый со стороной 9 и два со стороной 8 — и клетки, расположенные по незакрашенной главной диагонали квадрата 16´16, содержащего квадраты 8´8. Тогда на доске можно будет выделить 48 не пересекающихся квадратов 2´2, все клетки которых закрашены. Поэтому в этом примере надо перекрасить не менее 48 клеток.
10. Докажите, что существует натуральное число n, большее 10100, такое, что сумма всех простых чисел, меньших n, взаимно проста с n. (Р. Салимов)
Решение. Обозначим через S (n) сумму всех простых чисел, меньших n. Заметим, что
S (n) < 1+2+…+(n –1) = n (n –1)/2 < n (n –1) (*).
Рассмотрим два последовательных простых числа q > p > 10100. Допустим, S (p) не взаимно просто с p, а S (q) не взаимно просто с q. Тогда S (p) делится на p, а S (q) делится на q. Пусть S (p) = kp. Из неравенства (*) вытекает, что k < p –1. Тогда, так как S (q) = S (p)+ p = p (k +1), и S (q) делится на q, имеем k +1 ³ q. Но k < p –1 < q –1. Противоречие.