При изучении фильтрации флюидов в трещиноватых породах в нефтегазовой подземной гидромеханике рассматривают две модели пород: трещиноватые и трещиновато-пористые (рис.1).
Рис.1 Схемы чисто трещиноватой (а) и
тещиновато-пористой (б) сред:
1,3 – трещины; 2 – пористые блоки.
В чисто трещиноватых средах (рис.1,а) блоки породы, расположенные между трещинами непроницаемы, движение жидкости и газа происходит только по трещинам.
Трещиновато-пористая среда (рис.1,б) - это совокупность пористых блоков, отделенных друг от друга трещинами. Жидкость и газ заполняют и трещины и поры. При этом размеры трещин во много раз больше размеров пор, так, что проницаемость системы трещин k1 значительно больше, чем проницаемость системы пор в блоках k2. В то же время коэффициент трещиноватости m1 – отношение объема, занятого трещинами, к общему объему – существенно меньше пористости блоков m2. Коэффициент трещиноватости составляет обычно доли процента, а коэффициент пористости блоков – 10-20%. Коэффициенты проницаемости k1 и трещиноватости m1 зависят от густоты и раскрытия трещин. Густотой трещин Г называется число трещин n, отнесенное к длине нормали, проведенной к поверхностям, образующим трещины.
Рассмотрим модель чисто трещиноватой среды с упорядоченной системой параллельных и равноотстоящих трещин с раскрытием δ (рис. 2).
Рис.2 Модель трещиноватой среды
с упорядоченной системой трещин
Густота трещин - 
, коэффициент трещиноватости - 
.
Если в пласте имеется две взаимно-перпендикулярные системы трещин с одинаковой густотой и раскрытием, то m1=2Гδ; если три, то m1=3Гδ. В общем случае можно записать
, (1)
где Θ – безразмерный коэффициент, зависящий от геометрии системы трещин в породе.
Движение жидкости или газа в трещине можно представить, как движение в узкой щели шириной δ, где средняя скорость движения определяется по формуле Буссинеска:
.
Перейдя к скорости фильтрации, получим:
. (2)
Сопоставив формулу (2) с законом Дарси и использовав соотношение (1), найдем выражение для коэффициента проницаемости трещиноватой среды:
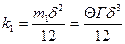. (3)
Если считать, что деформации в трещиноватом пласте упругие и малы по величине, то зависимость раскрытия трещины от давления можно считать линейной:
, (4)
где β – параметр трещиноватой среды, зависящий от геометрии трещин и упругих свойств породы.
Исходя из формул (3) и (4), можно записать зависимость для коэффициента проницаемости от давления в виде:
. (5)
Так же для коэффициента проницаемости используется экспотенциальная зависимость:
, (6)
Которая при малых изменениях давления имеет вид
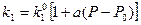, (7)
где а=3δ.
При рассмотрении фильтрации в трещиновато-пористой среде считают, что коэффициент проницаемости трещин k1 существенно зависит от давления и определяется по одной из формул (5)-(7), а коэффициент проницаемости пористых блоков k2 не зависит от давления и принимается постоянным.
При составлении математической модели фильтрации в трещиноватых средах считают, что в каждой точке имеется два давления (Р1 в системе трещин и Р2 в пористых блоках) и две скорости фильтрации - w1 и w2 соответственно. Между средами происходит обмен жидкостью пропорциональный разности давлений. Для слабосжимаемой жидкости количество жидкости q, перетекающей за единицу времени из блоков в трещины, определяется зависимостью
, (8)
где а0 – безразмерный коэффициент, зависящий от геометрических характеристик блоков. Для газов интенсивность перетоков имеет вид
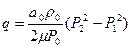. (9)
Уравнение неразрывности фильтрационного потока имеет вид:
в трещинах
, (10)
в пористых блоках
. (11)
Для чисто трещиноватой среды q=0 и остается только уравнение (10), так как вся жидкость находится в трещинах.
Закон фильтрации Дарси записывается для системы трещин
(12)
и пористых блоков
. (13)
Следует отметить, что, как и при фильтрации в пористой среде, закон Дарси имеет границы применимости. В трещиноватых породах, где истинное сечение потока мало, а дебиты велики, может использоваться двучленный закон фильтрации.
Рассмотрим установившуюся плоскорадиальную фильтрацию несжимаемой жидкости в чисто трещиноватом однородном пласте.
Условием неразрывности является условие постоянства объемного расхода
. (14)
Закон фильтрации
. (15)
Пусть проницаемость определяется соотношением (6), а μ=const.
На контуре питания и галерее поддерживается постоянное давление
Р(rc)=Pc, при r=rc;
Р(Rk)=Pk, при r=Rk. (16)
Уравнение (16) после подстановки в него скорости фильтрации из уравнения (14) и проницаемости (6) примет вид
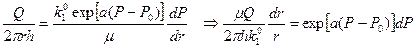. (17)
Интегрируя это уравнение в пределах от rc до Rk по радиусу и от P c до Pk по давлению, получим уравнение для расхода
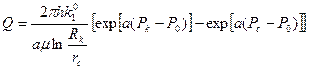. (18)
Если принять Р0=Рк то уравнение (18) упростится
. (19)
Проинтегрировав уравнение (17) в пределах r до Rk по радиусу и от P до Pk по давлению, получим закон изменения давления в пласте (при Р0=Рк)
. (20)