Оглавление
Введение........................................................................................................................................ 3
Свойства операционного усилителя........................................................................................... 3
Моделирование операционного усилителя в MATLAB.......................................................... 9
Активныефильтры..................................................................................................................... 13
Фильтр нижних частот........................................................................................................... 13
Фильтр верхних частот........................................................................................................... 18
Режекторный фильтр.............................................................................................................. 21
Полосовой фильтр................................................................................................................... 25
Лабораторная установка и выполнение измерений................................................................ 28
Задания......................................................................................................................................... 30
Литература................................................................................................................................... 31
Введение
Целью данной работы является изучение основных принципов действия активных фильтров, построенных на базе операционных усилителей. Подбором свойств цепи обратной связи можно реализовать фильтры различных типов: нижних и верхних частот, полосовые и режекторные.
В процессе выполнения предыдущих лабораторных работ были изучены свойства фильтров, построенных на базе пассивных RC-элементов. В курсе лекций также было показано что, используя различные комбинации включения пассивных звеньев первого и второго порядков, можно, в принципе, реализовать практически любую амплитудно-частотную и фазо-частотную характеристики, удовлетворяющие условиям физической осуществимости. Однако при этом следует иметь в виду следующие обстоятельства. Во-первых, при простом каскадном соединении RLC-звеньев коэффициент передачи цепи не будет равен произведению коэффициентов отдельных каскадов, так как входное сопротивление последующего звена будет служить нагрузкой для предыдущего. Если же желательно получить их произведение, то между ними необходимо включать разделительные каскады с большим входным и малым выходным сопротивлением. Во-вторых, в состав цепей, имеющих резкие экстремумы АЧХ, входят катушки индуктивности, технология изготовления которых не отвечает современным требованиям миниатюризации. Отмеченные трудности могут быть преодолены при использовании активных фильтров.
В ходе выполнения работы студенту предлагается рассчитать различные фильтры, провести компьютерное моделирование, смонтировать электрическую цепь и провести экспериментальные измерения. В данном описании приведены только основные теоретические результаты и метод создания блока операционного усилителя в Simulink для проведения дальнейшего численного моделирования. Более подробную информацию можно найти в методическом пособии «Применение операционных усилителей для фильтрации, генерации и усиления сигналов. Моделирование в Simulink».
Свойства операционного усилителя
Операционный усилитель (ОУ) представляет собой усилительное устройство с большим коэффициентом усиления К0 (103 ÷ 105), большим входным (до сотен МОм) и малым выходным (десятки Ом) сопротивлениями и широкой полосой пропускания, начинающейся от нуля и достигающей для ряда ОУ значения сотен мегагерц. На электрических схемах ОУ обычно изображается треугольником и имеет два входа (1 и 2 на Рис. 1) и один выход (5). ОУ выполняются в виде интегральных микросхем, в состав которых входят несколько десятков или сотен транзисторов.

Рис. 1. Изображение операционного усилителя.
Очевидно, что для того чтобы на работу усилителя не влиял источник сигнала, его выходное сопротивление должно быть существенно меньше входного сопротивления усилителя. Следствием этого является то, что входной ток усилителя очень мал. Если считать, что выходное сопротивление источника задано, то нужно стремиться к увеличению входного сопротивления усилителя. В идеале  .
.
Чтобы на работу усилителя не влияла нагрузка, ее сопротивление должно быть много больше выходного сопротивления усилителя, т.е. выходное сопротивление усилителя должно быть мало:  .
.
Если подать гармоническое напряжение x+(t) на вход (+) ОУ при заземленном втором входе, то на выходе будет напряжение K0 x+(t). Этот вход называется неинвертирующим. При подаче напряжения x-(t) на вход (–) на выходе получается напряжение -K0 x-(t). Этот вход называется инвертирующим. Следовательно, ОУ усиливает разность сигналов x+(t) и x-(t) на его входах.
На Рис. 1 отмечены спектральные функции входных сигналов X+(iω), X-(iω) и выходного сигнала Yвых(iω). Учитывая, что коэффициент передачи операционного усилителя K0, можно записать:
 . (1)
. (1)
Поэтому такой усилитель называется дифференциальным.
В идеальном случае, если оба входа имеют одинаковый потенциал относительно «земли» (общей точки), т.е. если дифференциальное входное напряжение равно нулю, то напряжение на выходе усилителя также равно нулю, независимо от коэффициента усиления схемы.
Наличие двух входов у дифференциального усилителя дает возможность включения двух независимых цепей обратной связи, одна из которых связывает выход усилителя с его инвертирующим входом, а другая – с неинвертирующим.
Чтобы обеспечить возможность работы ОУ как с положительными, так и с отрицательными входными сигналами, используется двухполярное постоянное питающее напряжение (на Рис. 1 оно подключается к 3 и 4 выводам ОУ).
Рассмотрим некоторые параметры ОУ:
1. Дифференциальный коэффициент усиления по напряжению является комплексной величиной  . Модуль коэффициента усиления К0 – это отношение амплитуды сигнала на выходе к амплитуде дифференциального входного напряжения (для гармонических сигналов). Типовые значения К0 находятся в пределах 103 – 105.
. Модуль коэффициента усиления К0 – это отношение амплитуды сигнала на выходе к амплитуде дифференциального входного напряжения (для гармонических сигналов). Типовые значения К0 находятся в пределах 103 – 105.
2. Частота единичного усиления f1. На больших частотах усиление ОУ снижается. При некоторой частоте входного сигнала усиление ОУ уменьшается до 1. Эта частота называется частотой единичного усиления. Для низкочастотных ОУ f1 = 1МГц, для быстродействующих высокочастотных f1 = 15 – 100 МГц.
3. Входное сопротивление – сопротивление со стороны любого входа, в то время как другой вход заземлен. Входное сопротивление может для разных типов усилителей иметь величину от нескольких кОм до нескольких сотен мОм.
4. Выходное сопротивление – это сопротивление со стороны выхода в таком режиме работы, когда напряжение на входе равно нулю. Это сопротивление может быть равно 25 – 500 Ом.
5. Полоса пропускания ОУ определяется как частотный диапазон, в котором выходное напряжение уменьшается не более чем до 0,707 от своего максимального значения при неизменной амплитуде на входе. Нижняя граница полосы пропускания равна нулю (ОУ усиливают постоянные напряжения), верхняя граница полосы пропускания определяется типом ОУ и может изменяться от десятков кГц до сотен МГц.
6. Выходное напряжение сдвига – это напряжение на выходе ОУ относительно «земли» или общей точки схемы при условии, что дифференциальное входное напряжение равно нулю. Операционные усилители конструируются так, чтобы это напряжение было равно нулю. Однако практически точно выполнить это условие невозможно. Обычно, для установления выходного напряжения, равного нулю, необходимо подать на вход (между выводами «+» и
«-») несколько милливольт. Некоторые ОУ имеют выводы для подключения потенциометра, регулирующего напряжение на выходе при отсутствии входного сигнала.
7. Входное напряжение смещения – напряжение, которое нужно приложить между входами усилителя для получения нуля на выходе. Эта величина чаще всего лежит в диапазоне 0 – 10 мВ.
8. Максимальное выходное напряжение – амплитуда выходного напряжения относительно нуля при работе усилителя на линейном участке. У разных типов ОУ максимальное выходное напряжение лежит в диапазоне ±(3 – 15) В.
Для расчетов схем с ОУ широко используют понятие об идеальном операционном усилителе, подразумевая под этим, что у ОУ:
o коэффициенты усиления по току и напряжению и входное сопротивление каждого из входов ОУ бесконечно велики;
o усилитель полностью симметричен, не имеет дрейфа нуля и усиливает одинаково колебания любых частот. Дрейфом нуля называется изменение выходного напряжения, не связанные со входным сигналом и обусловленные внутренними процессами в усилителе. Главная причина дрейфа – изменение температуры.
На практике вследствие разбаланса и несимметрии дифференциальных усилителей внутри самого ОУ на выходе будет наблюдаться некоторое напряжение сдвига даже в том случае, когда оба его входа заземлены. Это напряжение может быть настолько большим, что ОУ войдет в режим насыщения и как усилительный элемент работать не будет. Компенсация выходного сдвига называется балансировкой усилителя. Для этого на один из входов подают небольшое постоянное напряжение. Величина и полярность этого напряжения может быть разной для различных схем включения ОУ. Поэтому в схемах балансировки ОУ используются потенциометры, подключенные так, как показано на Рис. 2 и Рис. 3.

Рис. 2. Схема балансировки инвертирующего усилителя.

Рис. 3. Схема балансировки неинвертирующего усилителя
В некоторых ОУ предусмотрены специальные выводы для установки нуля. Изготовители рекомендуют подключать потенциометры между выводами «балансировка» (Б1 и Б2), как показано на Рис. 4. Как правило, в этом случае балансировка осуществляется в коллекторных и эмиттерных цепях усилительных транзисторов первого дифференциального каскада.
Помимо напряжения сдвига, разбаланс усилителя может быть вызван так называемыми токами смещения. Транзисторам как приборам, управляемым током, для базового смещения необходим некоторый ток. Поэтому через входные клеммы типичного ОУ протекают небольшие постоянные токи смещения. Величина входного тока обычно мала (она указывается в справочниках). Однако при использовании в цепи обратной связи резисторов с относительно большими сопротивлениями наличие токов смещения может привести к переходу ОУ в насыщенный режим работы.

Рис. 4. Схема ОУ.
Действительно, при обычном включении ОУ Рис. 5 напряжение на входе «+» равно нулю, а на выходе «-» отлично от нуля, т. к. базовый ток смещения встречает на своем пути ко входу «-» сопротивление, равное параллельно соединенным сопротивлениям R1 и R2.

Рис. 5. Токи смещения I1 и I2 на входах ОУ.
Таким образом, между входами ОУ образуется дифференциальное напряжение, которое усиливается и приводит к появлению выходного напряжения сдвига. Очевидно, что это напряжение тем больше, чем больше сопротивления, используемые в цепи обратной связи.
Влияние входного тока смещения на выходное напряжение сдвига можно свести к минимуму, если включить, как показано на Рис. 6, последовательно с неинвертирующим входом резистор R3, сопротивление которого определяется по формуле
 .
.
В этом случае если базовые токи транзисторов дифференциального каскада одинаковы, то дифференциальное входное напряжение, обусловленное токами смещения, будет равно нулю. Если же они не одинаковы, то для уменьшения влияния токов смещения необходимо уменьшать сопротивления в цепи обратной связи.
Прежде чем перейти к рассмотрению конкретных схем включения ОУ, уточним, в каких случаях при расчете внешних элементов можно пользоваться понятием идеальности ОУ. Очевидно, что током во входной цепи усилителя (Рис. 5) можно пренебречь, если входное сопротивление ОУ много больше сопротивления параллельно соединенных R1 и R2; коэффициент усиления по напряжению можно считать бесконечным, если он много больше требуемого коэффициента усиления, определяемого цепью обратной связи; выходное сопротивление можно считать бесконечно малым, если оно много меньше сопротивления нагрузки усилителя.

Рис. 6. Схема балансировки усилителя.
Итак, при всех расчетах, которые проводятся в предположении идеальности ОУ, следует выбирать такие сопротивления, чтобы выполнялись следующие условия:
 ;
;  ;
; 
Моделирование операционного усилителя в MATLAB
Перед выполнением эксперимента необходимо рассчитать параметры схемы и провести компьютерное моделирование. В данной работе для моделирования предлагается использовать библиотеку SimPowerSystems программы Simulink.
В библиотеке SimPowerSystems нет специального блока для операционного усилителя, но пользователь имеет возможность создать свой собственный блок, собрав его схму замещения из блоков вольтметров, источника напряжения и блоков основной библиотеки Simulink. Рассмотрим, какой моделью можно описать ОУ. Исходя из частотных свойств, ОУ является фильтром низких частот с широкой полосой пропускания. Поэтому моделировать частотные свойства ОУ будем с помощью функции передачи фильтра низких частот и коэффициента усиления:
 , (2)
, (2)
где K0 – коэффициент передачи ОУ на постоянном токе (коэффициент усиления). Модуль передаточной функции (2) будет:

Учитывая, что на частоте единичного усиления f1 модуль коэффициента передачи равен единице, находим постоянную времени цепочки τ:
 . (3)
. (3)
Обычно коэффициент усиления K0 очень большой, поэтому единицей в числителе выражения (3) можно пренебречь. Тогда, коэффициент передачи (2) можно переписать как:
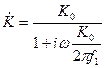 (4)
(4)
Таким образом, функция передачи ОУ будет описываться двумя параметрами K0 и f1. Для типичных значений K0 =105 и f1 =108/2π Гц зависимость модуля (Magnitude) и фазы (Phase) комплексной функции передачи от частоты (Frequency) будет выглядеть следующим образом (Рис. 7). Для наглядности графики приведены в логарифмическом масштабе. Видно, что при циклической частоте ω1 = 108 рад/с модуль функции передачи равен 1.
Рассмотрим модель ОУ в SimPowerSystems (Рис. 8). Взаимодействие усилителя с электрической цепью происходит через клеммы 1, 3, обозначенные соответственно «+» и «-» (вход ОУ), и клемму 2, обозначенную «out» (выход ОУ). Соединение с Simulink -моделью осуществляется с помощью двух блоков измерителей напряжения Voltage Measurement (свой для каждого входа) и блока управляемого источника напряжения Controlled Voltage Source. Три сопротивления на схеме моделируют входные сопротивления ОУ (по каждому входу) и выходное сопротивление ОУ. Основу модели составляет схема из блоков Simulink.

Рис. 7. АЧХ и ФЧХ модели ОУ.

Рис. 8. Модель ОУ.
Коэффициент передачи ОУ на постоянном токе задает усилитель Gain (коэффициент усиления в окне параметров блока задается переменной K0), на вход которого поступает разность входных напряжений усилителя с блока Add.
Блок передаточной функции Transfer Fcn задает частотные свойства операционного усилителя (вектор числителя блока [1], а знаменателя [K0/2/pi/f1 1]), а блок насыщения Saturation обеспечивает ограничение выходного напряжения на уровне напряжений положительной и отрицательной полярностей (величины насыщения в свойствах блока обозначены переменными lim и -lim), имитируя нелинейность характеристики реального усилителя вызванную, конечной величиной напряжений питания.
Оформим модель ОУ как отдельный блок, чтобы его можно было в дальнейшем использовать для моделирования различных электрических схем. Для этого создадим маскированную подсистему, отражающую общепринятое условное обозначение ОУ в схеме и параметры, характеризующие модель ОУ. Окно с вкладкой Icon, описывающей внешний вид блока показано на Рис. 9. Здесь в основном окне введена команда MATLAB plot, соединяющая прямыми отрезками точки, координаты которых указаны в параметрах команды.

Рис. 9. Окно с вкладкой Icon редактора маски ОУ.
В данном случае, это вектор координат X [10 10 40 10] и соответствующий вектор координат Y [10 20 15 10]. Эта команда рисует треугольник. Чтобы не было видно контура границы самой иконки подсистемы, в окне Frame была выбрана опция Invisible (невидимый). Для того чтобы были видны порты подсистемы и их обозначения на иконке, в окне Transparency выбирается опция Transparent (прозрачный).
Окно параметров Parameters показано на Рис. 10. Здесь введены основные параметры, описывающие модель ОУ:
o gain – коэффициент передачи на постоянном токе;
o unit frequency – частота единичного усиления;
o saturation – пределы насыщения (усилитель симметричный).

Рис. 10. Окно с вкладкой Parameters редактора маски ОУ.

Рис. 11. Иконка ОУ и окно параметров ОУ.
После создания маски блок ОУ будет выглядеть, как показано на Рис. 11. На этом же рисунке приведено окно параметров этого блока, оно будет открываться при двойном щелчке по иконке блока вместо схемы подсистемы. В приближении идеального ОУ можно упростить схему
Рис. 8.
Можно отказаться от резисторов считая, что входное сопротивление идеального ОУ бесконечно велико, а выходное – бесконечно мало. Также, если не учитывается частотная зависимость, можно исключить блок передаточной функции.
Активныефильтры
При работе с электрическими сигналами часто требуется выделить из них какую-либо одну частоту или полосу частот (например, разделить шумовой и полезный сигналы). Для подобного разделения используются электрические фильтры. Активные фильтры, в отличие от пассивных, включают в себя ОУ (или другие активные элементы, например, транзисторы, электронные лампы) и обладают рядом преимуществ. Они обеспечивают более качественное разделение полос пропускания и затухания, в них сравнительно просто можно регулировать неравномерности частотной характеристики в области пропускания и затухания. Также в схемах активных фильтров обычно не используются катушки индуктивности. В схемах активных фильтров частотные характеристики определяются частотнозависимыми обратными связями.
Фильтр нижних частот
Схема фильтра нижних частот приведена на Рис. 12.

Рис. 12. Активный фильтр нижних частот.
Коэффициент передачи такого фильтра можно записать как
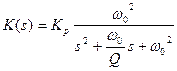 , (5)
, (5)
где
 и
и  . (6)
. (6)
При К0 >>1

Коэффициент передачи  в (5) оказывается таким же, как и у пассивного фильтра второго порядка, содержащего все три элемента (R, L, C) (Рис. 13), для которого:
в (5) оказывается таким же, как и у пассивного фильтра второго порядка, содержащего все три элемента (R, L, C) (Рис. 13), для которого:

|  . .
|
| Рис. 13. Пассивный RLC -фильтр нижних частот |

Рис. 14. АЧХ и ФЧХ активного фильтра низких частот для разных Q.
Если R1 = R3 = R и C2 = C4 = С (на Рис. 12), то коэффициент передачи можно записать как

Амплитудно- и фазочастотные характеристики активного фильтра низких частот для разных значений добротности Q показаны на Рис. 14 (параметры электрической схемы подобраны так, чтобы ω0 = 200 рад/с). Из рисунка видно, что с ростом Q проявляется резонансный характер амплитудно-частотной характеристики.
Активный фильтр низких частот первого порядка реализуется схемой Рис. 15.

Рис. 15. Активный фильтр низких частот первого порядка.
Коэффициент передачи фильтра равен
 .
.
Пассивный аналог этого фильтра представлен на Рис. 16.

|  . .
|
| Рис. 16. Пассивный фильтр низких частот первого порядка. |
Сравнивая эти коэффициенты передачи, видим, что при одинаковых постоянных времени τ’2 и τ модуль коэффициента передачи активного фильтра первого порядка будет в К0 раз больше, чем у пассивного.

Рис. 17. Simulink-модель активного фильтра низких частот.
Исследовать АЧХ и ФЧХ рассматриваемого активного фильтра можно, например, в Simulink, используя блок передаточной функции. Для параметров электрической схемы Кр = 1, ω0 = 200 рад/с и Q = 10 Simulink -модель с блоком передаточной функции будет выглядеть, как показано на Рис. 17. АЧХ и ФЧХ можно получить с помощью LTI-viewer. Но в данном случае проще использовать команду MATLAB freqs. Ниже приведен листинг для получения графиковАЧХ и ФЧХ.
w0=2e2; %собственная частота
Q=10; %добротность
w=0:1:400; %диапазон частот
b=[w0^2]; %вектор числителя передаточной функции:
a=[1 w0/Q w0^2]; %вектор знаменателя передаточной функции:
freqs(b,a,w); %расчет и построение АЧХ и ФЧХ
Амплитудно-частотные характеристики активного фильтра низких частот (для τ = 1с и К0 = 1000) показаны на Рис.18. Из рисунка видно, что с ростом Q проявляется резонансный характер амплитудно-частотной характеристики.
Построим модель фильтра нижних частот в SimPowerSystems, используя созданный нами блок ОУ (operational amplifier), как показано на Рис 19. Блок операционного усилителя является нелинейным, поэтому в настройках Simulation/Configuration Parameters Simulink для увеличения скорости расчета нужно использовать методы ode23tb или ode15s. Также необходимо разумно выбрать шаг по времени.

Рис. 18. АЧХ и ФЧХ активного фильтра низких частот (для τ = 1с).
Пусть R1 = R3 = R6 = 100 Ом, R5 = 190 Ом, C2 = C 4 = 5*10-5 Ф. Для случая, когда частота источника совпадает с собственной частотой системы ω0, сигнал на выходе фильтра достигает максимальной амплитуды (приведен на Рис. 20). Сигнал представляет собой установившиеся вынужденные колебания с частотой источника. На графике хорошо виден переходный процесс, вызванный включением схемы в момент времени t = 0. Также на графике видны отклонения сигнала от синусоидальной формы вблизи экстремумов. На Рис. 21. приведена увеличенная часть предыдущего графика. Эти отклонения можно объяснить насыщением ОУ (максимально допустимые значения напряжения на выходе ОУ ± 15 В). Очевидно, что при увеличении амплитуды сигнала источника увеличивается и область искажений сигнала на выходе
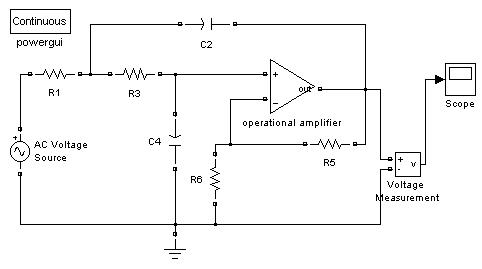
Рис. 19. Модель активного фильтра низких частот в SimPowerSystems.

Рис. 20. Сигнал на выходе активного фильтра низких частот.

Рис. 21. Фрагмент сигнала на выходе активного фильтра низких частот.
Фильтр верхних частот
Схема фильтра высоких частот второго порядка показана на Рис. 22.

Рис. 22. Активный фильтр высоких частот.
Выражение для коэффициента передачи такого фильтра записывается как:
 , (7)
, (7)
где при К0 >> 1
 ,
,  ,
,
 .
.
Если R2 = R4 = R и C1 = C3 = С, то коэффициент передачи можно записать как

Схема пассивного фильтра высоких частот второго порядка на RLC -элементах с аналогичной частотной характеристикой приведена на Рис. 23.

| Коэффициент передачи такого фильтра описывается выражением (7) со следующими значениями параметров:
 . .
|
| Рис. 23. Схема пассивного фильтра высоких частот второго порядка. |

Рис. 24. АЧХ и ФЧХ активного RC-фильтра высоких частот второго порядка.
Исследовать АЧХ и ФЧХ рассматриваемого фильтра можно также, как и в предыдущем случае в Simulink. Для параметров электрической схемы Кр = 1, ω0 = 200 рад/с вектор числителя передаточной функции будет b = [1 0 0] и вектор знаменателя a = [1 2e2/ Q 4e4]. Зависимость частотных характеристик от величины параметра Q показаны на Рис 24. В этом случае также параметры схемы подобраны так, чтобы собственная частота системы ω0 = 200 рад/с. После перевода в герцы f0 = 31.8310. Здесь также с увеличением Q АЧХ активного фильтра приобретает резонансный характер.
Активный фильтр высоких частот первого порядка изображен на Рис. 25., а его пассивный аналог – на Рис. 26.
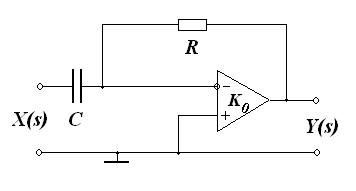
| Коэффициент передачи активного фильтра первого порядка равен:
 .(8) .(8)
|
| Рис. 25. Активный фильтр первого порядка высоких частот. |

| Коэффициент передачи пассивного фильтра:
 . .
|
| Рис. 26. Пассивный фильтр первого порядка высоких частот. |
Сравнивая приведенные выражения для коэффициентов передачи видим, что при одинаковых постоянных τ’1 и τ модуль коэффициента передачи активного фильтра в К0 раз больше, чем у пассивного.
Частотные характеристики активного фильтра высоких частот приведены на Рис 27. (для τ = 1с).

Рис. 27. АЧХ и ФЧХ активного фильтра высоких частот (для τ = 1с).
Режекторный фильтр
Режекторный фильтр с регулируемой полосой режекции может быть построен по схеме, приведенной на Рис. 28.
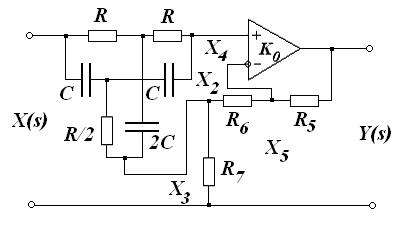
Рис. 28. Режекторный активный фильтр.
В этой схеме в цепи частотноизбирательной обратной связи включен сбалансированный двойной Т-образный RC -мост (Рис. 29).

Рис. 29. Сбалансированный двойной Т-образный RC -мост.
Коэффициент передачи Т-образного RC -моста в предположении, что мост не нагружен, равен
 . (9)
. (9)
Такое приближение может быть принято, т.к. входное сопротивление усилителя велико. Коэффициент передачи режекторного фильтра можно определить как:
 .
.
Выделим выражения, описывающие величину усиления, регулируемую соотношением сопротивлений в цепи обратной связи:
 .
.
Тогда коэффициент передачи можно переписать как:
 .
.
Используя выражение для β(s), получим
 .
.
Если  , то
, то  . Таким образом, в этом случае коэффициент передачи фильтра не зависит от К0 и определяется выражением
. Таким образом, в этом случае коэффициент передачи фильтра не зависит от К0 и определяется выражением
 . (10)
. (10)
Введя обозначения
 ,
,
приведем это выражение к стандартному виду
 .
.
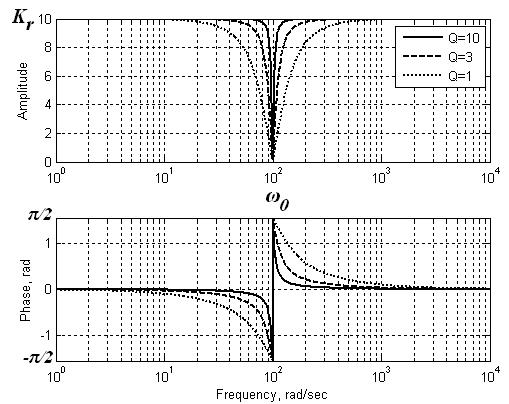
Рис. 29. АЧХ и ФЧХ активного режекторного RC -фильтра.
Семейство АЧХ и ФЧХ активного режекторного RC -фильтра при различных значениях Q приведены на (Рис. 29). Здесь для определенности выбраны значения Kr = 10, ω0 = 100 рад/с.
Полоса режекции определяется величиной Q и оказывается тем более узкой, чем больше Q. Существенно, что при любых значениях Кr режекторный активный фильтр остается устойчивым, т.к. всегда Q больше нуля. Если мост не сбалансирован (не точно выполняются соотношения между R и C в вертикальных и горизонтальных плечах моста (Рис.)), то режекция не является полной.
На Рис. 30. изображены характеристики для сбалансированного (пунктирная линия) и несбалансированного (сплошная линия) моста. Заметим, что мы описывали эту схему в предположении, что Т-образный мост не нагружен. Поэтому, для того чтобы результаты согласовывались с теоретическими результатами, выходное сопротивление Т-образного моста должно быть много меньше входного сопротивления усилителя и одновременно много больше сопротивления R7, через которое средняя точка моста подключена к земле.

Рис. 30. АЧХ и ФЧХ для сбалансированного и несбалансированного моста.
Модель активного режекторного RC -фильтра в SPS будет выглядеть, как показано на Рис 31.

Рис. 31. Модель активного режекторного RC -фильтра в SPS.
Полосовой фильтр
В отличие от режекторного, полосовой фильтр пропускает сигнал в определенном диапазоне частот. Рассмотрим два варианта реализации полосового фильтра. Первая схема приведена на Рис. 32.

Рис. 32. Активный полосопропускающий фильтр.
Выражение для коэффициента передачи в этом случае:
 , (11)
, (11)
где
 (12)
(12)
Вторая схема полосопропускающего фильтра показана на Рис. 33. Этот фильтр также имеет характеристику (11)., где теперь
 (13)
(13)

Рис. 33. Активный полосопропускающий фильтр.
Выражение (11) при К1 = 1 совпадает с коэффициентом передачи пассивного RLC -фильтра, собранного по схеме (Рис. 34.), со следующими параметрами:

 (14)
(14)
АЧХ и ФЧХ рассматриваемого активного полосопропускающего фильтра при разных Q приведены на (Рис. 35). Графики приведены для K1 = 10 и ω0 = 100 рад/с.
В отличие от характеристик рассмотренных выше фильтров низкой и высокой частоты данный фильтр за пределами полосы пропускания ослабляет сигналы как низких, так и высоких частот. При Q << 1 имеем фильтр с коэффициентом передачи, практически равным единице в широкой полосе (fн << fв). При Q >> 1 частотная характеристика фильтра имеет четко выраженный резонансный характер вблизи частоты ω0.

Рис. 34. Аналогичный RLC -фильтр.

Рис. 35. АЧХ и ФЧХ активного полосопропускающего фильтра.
Приведем примеры моделирования рассмотренных выше фильтров с помощью SimPowerSystems MATLAB. Модель для первой схемы показана на Рис. 36.
Так как схема может быть реализована не с любым набором параметров Q, ω0, K1, выберем для простоты расчета следующие параметры схемы:
Q = 2, ω0 = 100 рад/с, С1 = С2 = 10-6 Ф.

Рис. 36. Модель в SPS для первой схемы полосопропусающего фильтра.
Для второй схемы модель в SPS будет выглядеть, как показано на Рис. 37. Для удобства зададим параметры схемы Q = 2, ω0 = 100 рад/с, R3 = R2 = 103, C4 = 25 10-7 Ф, С1 = 4 10-5 Ф, К1 = 400.

Рис. 37. Схема в SPS для примера №2.