Группа: ЭМИ-12
Проверил: Кудряшов Г. П.
Вологда
Цель работы: определить коэффициент вязкости и длину свободного пробега молекул воздуха.
Оборудование: стеклянный сосуд с краном, пробка с капилляром, штатив, мерный стакан (колба), линейка, вода.
Теория вопроса.
Тепловое хаотическое движение молекул газа способствует сглаживанию всяких различий между равными частями газа. Поэтому если мы имеем слои газа, движущиеся с различными по величине скоростями, то на упорядоченное движение слоев газа с различными скоростями накладывается хаотическое движение молекул. Молекулы переходят из слоя, движущегося со скоростью  , в слой движущийся со скоростью
, в слой движущийся со скоростью  , и обратно, перенося при этом импульс. Такой процесс переноса количества движения (импульса), выравнивающий скорости отдельных слоев, сопровождается превращением кинетической энергии упорядоченного движения данного слоя в энергию теплового движения молекул и называется внутренним трением. Закон Ньютона для внутреннего трения имеет вид:
, и обратно, перенося при этом импульс. Такой процесс переноса количества движения (импульса), выравнивающий скорости отдельных слоев, сопровождается превращением кинетической энергии упорядоченного движения данного слоя в энергию теплового движения молекул и называется внутренним трением. Закон Ньютона для внутреннего трения имеет вид:

 (1)
(1)
Этот закон можно вывести, используя основные положения молекулярно-кинетической теории. Пусть у нас имеются два слоя газа, движущиеся со скоростями  и
и  .
.
Количество движения, переносимое потоком молекул в положительном направлении оси Z из слоя, движущегося со скоростью  равно:
равно:

где  – средняя арифметическая скорость.
– средняя арифметическая скорость.
Количество движения, переносимое потоком молекул в противоположном направлении, равно:

Изменение импульса слоя  выразиться:
выразиться:
 (2)
(2)
Учитывая, что  (плотность вещества), а разность скоростей
(плотность вещества), а разность скоростей  можно выразить через градиент скорости и длину свободного пробега
можно выразить через градиент скорости и длину свободного пробега 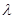 :
:

то выражение (2) примет вид:
 (3)
(3)
Известно, что изменение импульса тела определяется импульсом силы:  , тогда сила трения будет равна:
, тогда сила трения будет равна:
 (4)
(4)
В полученном выражении силы произведение  представляет собой динамический коэффициент вязкости:
представляет собой динамический коэффициент вязкости:
 (5)
(5)
Впредлагаемом методе определения динамического коэффициента вязкости используется истечение воздуха через капилляр.
Известно, что скорости истечения бесконечно тонких цилиндрических слоев воздуха, расположенных на различных расстояниях от оси капилляра, различны и распределены по сечению капилляра по параболическому закону. Наибольшая скорость будет на осевой линии капилляра, и, по мере приближения к стенкам, скорость уменьшается, а слой, прилегающий к стенке, неподвижен, т.е. “прилипает” к ней.
Между слоями, движущимися с различными скоростями, возникает сила внутреннего трения (сила вязкости). При установившемся движении сила вязкости, действующая на элементарный объем и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давлении, действующих на основание цилиндра. На концах капилляра при протекании по нему воздуха возникает разность давлений ( входа –
входа –  выхода). При установившемся движении воздуха она будет неизменной. При малых скоростях течения объем воздуха, протекающего через сечение капилляра, равен:
выхода). При установившемся движении воздуха она будет неизменной. При малых скоростях течения объем воздуха, протекающего через сечение капилляра, равен:

 (6)
(6)
Здесь r – радиус капилляра;  – динамический коэффициент вязкости;
– динамический коэффициент вязкости;  – разность давлений в начале капилляра и в конце; l – длина капилляра; V – объем газа, протекшего через сечение капилляра за время t.
– разность давлений в начале капилляра и в конце; l – длина капилляра; V – объем газа, протекшего через сечение капилляра за время t.
 Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра.
Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра.
 Схема установки представлена на рис. 2 и состоит из стеклянного сосуда А со шкалой. Верхняя часть сосуда закрыта пробкой с капилляром, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на
Схема установки представлена на рис. 2 и состоит из стеклянного сосуда А со шкалой. Верхняя часть сосуда закрыта пробкой с капилляром, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на  объема и плотно закрыт пробкой с капилляром. Если открыть кран k, то по истечении некоторого времени вода из сосуда А будет вытекать каплями. При объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление у открытого конца трубки D равно сумме давлений: воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления
объема и плотно закрыт пробкой с капилляром. Если открыть кран k, то по истечении некоторого времени вода из сосуда А будет вытекать каплями. При объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление у открытого конца трубки D равно сумме давлений: воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления  ,
,  . Это давление уравновешивается атмосферным
. Это давление уравновешивается атмосферным 
Учитывая, что давление у верхнего конца капилляра равно атмосферному, разность давлений на концах капилляра выразиться:

Поскольку, в процессе опыта давление столба воды уменьшается (за счет истечения), то берут среднее значение:

и выражение для вязкости примет вид:
 (7)
(7)
Если учесть, что  , а
, а  , то для средней длины свободного пробега молекул получим выражение:
, то для средней длины свободного пробега молекул получим выражение:
 (8)
(8)
Здесь P – атмосферное давление; R – газовая постоянная;  – молярная масса.
– молярная масса.
Измерение и обработка результатов.
| № | V | D V | t | D t | 
| 
| D h | h | D h | 
|

| 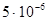
| 75,48 | 0,1 | 0,26 | 0,24 | 0,005 | 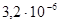
| 
| 0,09 | |
| 75,17 | 0,24 | 0,22 | 
| |||||||
| 75,62 | 0,22 | 0,2 | 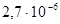
|
| l | D l | 
|

| 
| 0,07 |

| ||

|
 ;
;  ;
;  ;
;
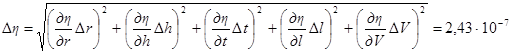 ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  .
.
Вывод: мы определили коэффициент вязкости и длину свободного пробега молекул воздуха.