Рассмотрим старую Задачу. Производится п независимых повторных испытаний (опытов). Вероятность удачи при каждом испытании р, вероятность неудачи – q. (р+q=1). Пусть m – число удач. Требуется найти вероятность того, что в серии из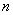 
независимых испытаний, расхождение между относительной частотой и теоретической вероятностью 
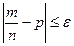, где 
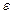- заранее заданное число, относительная погрешность, например, не больше, чем 
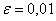(один процент).
В лекции 3 была интегральная формула Лапласа
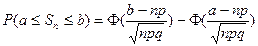, (1)
Где 
. (2)
В нашем случае 
, тогда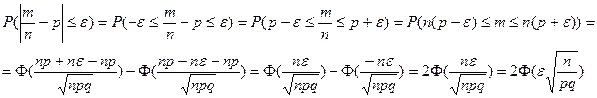 
.
Итак, (3)
, где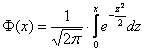 
Функция Лапласа.
Задача 1
В некотором регионе в результате многолетнего статистического исследования установлена вероятность рождения мальчика 
. С какой вероятностью можно утверждать, что среди следующей тысячи новорожденных, относительная частота появления мальчика отклонится от соответствующей вероятности не более чем на 0,02?
Решение: используем формулу
По условию: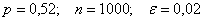 
Таким образом:
– искомая вероятность.
Напоминаю, что значения функции Лапласа можно найти по соответствующей таблице 2 в Гмурмане.
Ответ: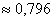 
Каков смысл полученного результата? Если рассмотреть достаточно много групп по 1000 новорожденных в каждой, то примерно в 79,6% этих групп доля мальчиков будет находиться в пределах:
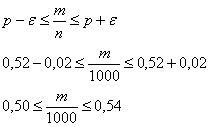
Или, умножая все три части на тысячу: от 500 до 540 мальчиков.
Посмотрим на правую часть формулы и проанализируем, как при прочих равных условиях рассматриваемая вероятность зависит от размера выборки?
При росте «эн», дробь 
будет увеличиваться, а, как вы знаете, 
. То есть, вероятность отклонения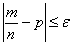 
рано или поздно приблизится к единице. И это неудивительно – как неоднократно показано в предыдущих примерах, при росте 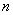относительная частота события 
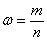всё ближе и ближе стремится к вероятности 
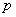данного события, а значит, при достаточно большом количестве испытаний разница 
практически достоверно будет не больше наперёд заданного числа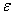 
.
Наоборот – при уменьшении «эн» дробь тоже будет уменьшаться, следовательно, значение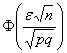 
будет приближаться к нулю 
. Нетрудно понять, что при слишком малой выборке теорема Лапласа работать перестанет. И действительно – ведь все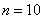 
детей в семье могут вообще оказаться девочками. Такое бывает.
Пара задач для самостоятельного решения:
Задача 2
Вероятность выигрыша в лотерею равна 0,3. Сколько билетов должно участвовать в розыгрыше, чтобы с гарантией не меньшей чем γ=99%/, можно было ожидать, что относительная частота выигрыша отклонится от теоретической вероятности не более чем на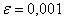 
?
Решение: используем ту же формулу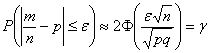 
.
В нашем распоряжении находятся следующие величины:
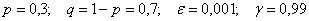
По условию, требуется найти такое количество билетов 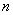, чтобы с вероятностью не меньшей чем 
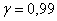разница составила не более чем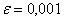 
. Ну, а коль скоро с вероятностью «не меньшей», то задачу следует разрулить через нестрогое неравенство:
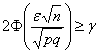
Подставляем известные значения:
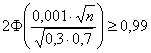Делим обе части на два:
По таблице значений функции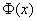 
по известному значению функции 
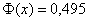находим соответствующий аргумент: 
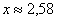. Таким образом:
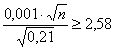
Возведём обе части в квадрат:
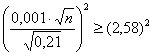
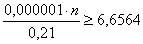
И финальный штрих:
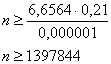
Ответ: для того, чтобы с надёжностью не меньшей чем γ=99% можно было ожидать, что 
, в розыгрыше должно участвовать не менее 1397844 билетов.
Но это ещё нужно столько продать =) Или же аппетит 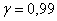придётся поубавить. Или пожертвовать точностью, то есть увеличить .
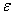Представим ответ в абсолютных значениях:
То есть, в 99% аналогичных розыгрышей количество выигравших билетов будет заключено в пределах от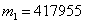 
до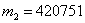 
.
Кстати, выполним проверку, решив прямую задачу:
, что и требовалось проверить.
Домашнее задание
Задача 1. Проводится некоторый опыт, в котором случайное событие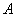 
может появиться с вероятностью 0,4. Определить, сколько опытов нужно провести, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события 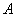от 
не более чем на 0,05
Задача 2. Решить задачу 1, если в рассмотренной задаче значение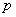не известно.
Задача 3. Гмурман задачник. № 135, 136 разобать.
Задача 5. Отдельные 2 сканированных файла. В задании 3 пункты 2 и 3 можно не делать, задание 4 – на будущее.