Предикаты, операции над ними
Опред. 1 Предложение, содержащее переменные и становящееся высказыванием при подстановке вместо переменных их значений, называется высказывательной формой или предикатом.
Опред. 2 Множество значений, которые может принимать переменная, называется областью определения предиката.
Каждый предикат разбивает область определения на два подмножества, на одном из которых он принимает значение И, а на другом Л.
Опред. 3 То подмножество области определения Р(х), на котором он принимает значение И, называется областью истинности предиката Р(х ) и будем записывать символически {х|Р(х)} или Тр.
Существуют двуместные Р(х; у), трехместные Р(х; у; z) …предикаты. Областью определения двуместного предиката является декартово произведение Х × У.
Опред. 4 Подмножество декартова произведения Х × У, на котором предикат Р(х; у), принимает значение И, является областью истинности этого предиката.
Р(х; у):у ≤ х
Опред. 5 Два предиката Р(х) и Q(х), заданные на одном и том же множестве U и имеющие одинаковые значения истинности, называются равносильными: Р(х) ≡ Q(х).
Р(х): «натуральное число х делится на 9»
Q(х): «Сумма цифр десятичной записи натурального числа делится на 9»
Логические операции над предикатами
Пусть Р(х) и Q(х) заданы на множестве U
Опред. 6 Отрицанием предиката Р(х) называется предикат Р(х), определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех значениях х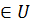 
, при которых Р(х) обращается в ложное высказывание
U
Тр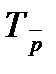 
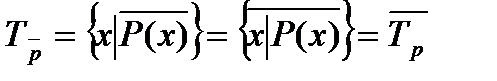
Опред. 7 Конъюнкцией предикатов Р(х) и Q(х) называется предикат Р(х) & Q(х), определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех х 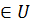, при которых оба предиката Р(х) и Q(х) одновременно обращаются в истинное высказывание.
Тр ТQ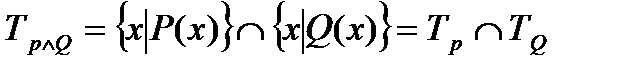 
Опред. 8 Дизъюнкцией предикатов Р(х) и Q(х) называется предикат Р(х) 
Q(х), определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех значениях х , при которых хотя бы один предикат обращается в истинное высказывание.
Тр ТQ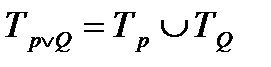 
Опред. 9 Импликацией предикатов Р(х) и Q(х) называется предикат Р(х) => Q(х), определенный на том же множестве и обращающийся в ложное высказывание при тех и только тех х , при которых Р(х) обращается в истинное высказывание, а Q(х) – в ложное.
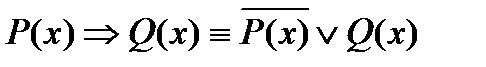
Тр ТQ
Опред. 10 Эквиваленцией предикатов Р(х) и Q(х) называется предикат Р(х) <=> Q(х), определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех х , при которых Р(х) и Q(х) обращаются оба в истинные или оба в ложные высказывания.
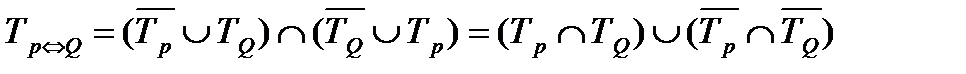
Тр ТQ
Преобразовать предикат в высказывание можно не только, подставив значение переменной. Существуют так называемые операции навешивания кванторов.
п. Р(х): натуральное число х – четное»
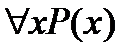- ложное высказывание
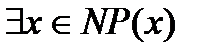- истинное высказывание
Опред. 11 Приписывание (спереди) к предикату квантора общности или существования называется операцией навешивания квантора, переменное х при этом называется связанной переменной.
Высказывание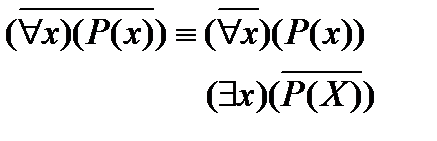 
- не для всех х выполняется свойство Р.
Итак, имеет место равенство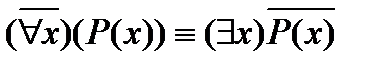 
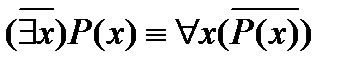
Вывод-правило: При отрицании высказывания с квантором квантор общности меняется на квантор существования и наоборот, а знак отрицания переносится на выражение, стоящее под знаком квантора.