Методика статистическо-типологического анализа историко-архитектурных материалов.
Историко-архитектурная статистика находится на начальной стадии развития.
Интенсивное применение специальных математических методов анализа информации в историко- архитектурной науке наблюдается только в последние 10 лет.
Трудности на пути развития историко-архитектурной статистики:
1. Архитекторы не обладают специальными математическими знаниями. Математики не обладают знанием предмета исследования (истории архитектуры).
2. Специальные математические руководства недоступны без специальной подготовки, а методические разработки биологов, медиков, социологов, историков могут быть использованы лишь в ограниченной степени.
Задачи, стоящие перед историко-архитектурной статистикой:
1. Разработка полного руководства по использованию статистических методов применительно к историко- архитектурной науке.
2. Детальное рассмотрение условий применимости статистических мер и вопросов проверки их значимости.
Выделяются 2 типа параметров:
- количественные;
- качественные.
Количественные методы могут быть применены только после того, как эмпирические данные переведены на язык чисел. Осуществить такой перевод можно с помощью такого понятия, как «измерение».
Измерение – познавательный процесс, в котором определяется отношение одной (измеряемой) величины к другой однородной величине, принимаемой за единицу измерения.
Пример.
Такое определение измерения применимо только для количественных признаков (время, геометрические размеры объектов, угол и т.п.), где имеются общепринятые единицы измерения (час, литр, градус и т.д.).
Для качественных признаков (взаимное расположение помещений, форма крыши и т.д.) таких эталонных единиц измерения нет. В этом случае под измерением понимается процедура приписывания чисел значениям параметра.
Цель измерения – получить числовую модель объекта исследования.
Пример.
Односкатная крыша – 1.
Двухскатная крыша – 2.
Здание, квадратное в плане – 1.
Здание, прямоугольное в плане – 2.
Модель объекта в цифровом выражении: 1,1; 1,2; 2,1; 2,2.
Числовая модель 2.1 означает квадратное в плане здание с двухскатной крышей.
Осуществить переход от графического образа объекта к его цифровой модели возможно только при условии, что объект обладает какими-либо свойствами (параметрами).
Набор свойств объекта и сопоставленных им чисел называется шкалой.
Пример.
Здание, квадратное в плане – 1.
Здание, прямоугольное в плане – 2.
Здание, круглое в плане – 3.
Все шкалы делятся на 4 типа:
- номинальные A, B, C, D;
- порядковые A ® B ® C ® D;
- интервальные A È B È C È D;
- шкалы отношений A/B = C/D.
Для построения номинальных шкал необходимо устанавливать отношения равенства (или неравенства) объектов для разделения изучаемой общности на непересекающиеся классы, каждый из которых является отдельным пунктом шкалы.
Свойства объекта не связаны между собой. Цифры можно менять местами.
Для построения порядковых шкал необходимо устанавливать не только отношения равенства между объектами по данному признаку, но и отношения последовательности.
Пример.
1 – одноэтажный дом
2 – двухэтажный дом
3 – трехэтажный дом
Достоинство: устанавливается порядок признаков.
Недостаток: порядок не является метрическим, т.е. нельзя сказать, насколько один вариант больше другого.
Для построения интервальных шкал используется эмпирическая процедура, позволяющая определить равенство дистанций между парами объектов.
Пример.
Расстояние между домами (дистанция составляет 5 метров).
1 – 0¸5 м
2 – 5¸10 м
3 – 10¸15 м
К интервальным относятся также координатно-пространственные, температурные и календарные шкалы.
В основе шкал отношений лежит эмпирическая процедура, позволяющая установить равенство отношений между парами объектов по изучаемому признаку.
Пример.
A/B = C/D
A – ширина 1 дома
B – ширина 2 дома
C – высота 1 дома
D – высота 2 дома
Этапы статистического анализа историко-архитектурных материалов
I этап. Табулирование и построение одномерных вариационных рядов.
Табулирование признака – построение матрицы данных.
Пример.
| № объекта | Значение признака |
| ….. | ….. |
Для большей наглядности далее подсчитывают сколько объектов обладают данным значением признака.
| Вариант | |||||
| Частота, n | |||||
| n/N | 0.15 | 0.25 | 0.03 | 0.35 | 0.22 |
| (n/N)100% |
Вариант – значение признака.
Частота (n) – число объектов, обладающих данным признаком.
N - общее число объектов.
Варианты и частота образуют вариационный ряд данного признака.
II этап. Построение полигонов и гистограмм распределения.
Если вариационный ряд большой, то глядя на него очень сложно увидеть существующие закономерности.
Поэтому далее всегда строят полигоны и гистограммы.
Полигоны и гистограммы строят процентные и с использованием частот. Процентные полигоны и гистограммы позволяют на первом этапе анализа представить общий характер распределения изучаемого признака.
Пример.
Полигон.
Гистограмма.
III этап. Построение двухмерных вариационных рядов (комбинационных таблиц).
Комбинационная таблица представляет собой два вариационных ряда.
На этом этапе осуществляется анализ распределения вариантов признака по территориальным и хронологическим ареалам.
Пример.
IY этап. Определение мер центральной тенденции.
Пример.
1. Анализируются 2 района.
2. Варианты признаков по районам распределены одинаково.
3. Варианты признаков по деревням распределены по разному.
| 1-этажный дом | 2-этажный дом | |
| Район 1 | ||
| Район 2 |
Среднее арифметическое М=åni/N
М1 = М2, но каждый из графиков имеет разный разброс. Следовательно, для оценки полигонов только величины среднего арифметического недостаточно.
В качестве дополнительной характеристики может использоваться мера, которая называется вариационный размах.
R=nmax-nmin
Но, эта мера определяется только крайними значениями признака и не отражает колебаний вариантов остальных признаков.
За меру колебаний вариантов принимают величину, называемую среднеквадратическим отклонением
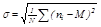
Среднеквадратическое отклонение – величина, показывающая, на сколько в среднем отклоняется каждый вариант от среднего арифметического.
Выводы:
1. Если у двух признаков одинаковые значения средних арифметических М, то колебания вариантов больше у того признака, у которого больше среднеквадратическое отклонение s.
2. Если средние арифметические М не равны, то для сравнения графиков используют
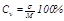 .
.
Колебания вариантов больше у того признака, у которого больше коэффициент вариации.
Y этап. Определение коэффициента ковариации.
Коэффициент ковариации является мерой типичности и уникальности.
Пример.
| 1 вариант | 2 вариант | |||||||
| Т | Т2 | Т3 | Т | Т2 | Т3 | |||
| Т2 и Т3 типичны | Т2 – типичен, Т3 - уникален |
| 3 вариант | |||
| Т | Т2 | Т3 | |
| Т2 – типичен, а Т3 –? |
Коэффициент ковариации
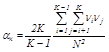 ,
,
где к – количество признаков;
n - частота признака;
N – общее количество частот признаков.
Пример.
| А | В | С |
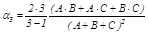
Пределы типичности:
- для двух признаков – 15 %;
- для трех признаков – 9,76 %;
- для четырех признаков – 8,17 %;
- для пяти признаков – 5,86 %.