ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«ЛУГАНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ИМЕНИ ВЛАДИМИРА ДАЛЯ»
Кафедра прикладной математики
Математическое моделирование
О Т Ч Ё Т
О выполнении практической работы № 5
СМО С ОЖИДАНИЕМ
Вариант № 0
Выполнил: студент группы
ФИО________________________
Дата сдачи____________________
Оценка______________________________
Проверил___________________________
Луганск, 2020
Выполнение работы
Краткие теоретические сведения.
Математическая модель работы СМО с ожиданием:
1) Система имеет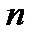 
, 
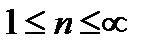, полнодоступных каналов обслуживания;
Возможные состояния системы:
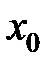– ни один канал не занятый (очереди нет),
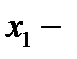занятый точно один канал (очереди нет),
…………………………………………………….
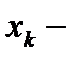заняты точно 
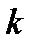каналов (очереди нет),
…………………………………………………….
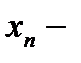заняты все 
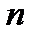каналов (очереди нет),
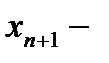заняты все 
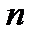каналов, одна заявка находится в очереди,
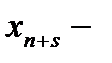заняты все 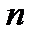каналов, 
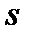заявок находится в очереди,
………………………………………………………..
2) Дисциплина обслуживания с ожиданием: вызов, заставший все каналы системы занятыми, становится в очередь и ожидает, пока не освободится какой-либо канал;
3) Закон распределения времени обслуживания одного вызова – экспоненциальный с параметром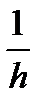 
, где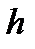 
– среднее время обслуживания одного вызова.
4) Входной поток вызовов простейший с плотностью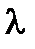 
, вероятность 
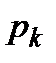состояния 
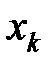(вероятность того, что заняты точно 
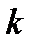каналов) вычисляется по формулам:
, 
.
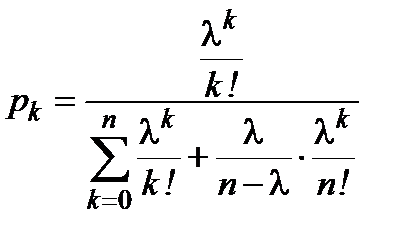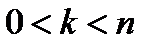Характеристики качества обслуживания СМО с ожиданием:
1. Интенсивность обслуженной нагрузки
.
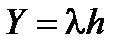2. Интенсивность потенциальной нагрузки
.
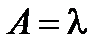3. Интенсивность поступающей нагрузки
.
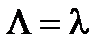4. Интенсивность утраченной нагрузки
.
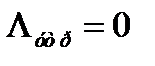5. Интенсивность избыточная
.
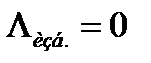6. Вероятность ожидания обслуживания поступивших вызовов
.
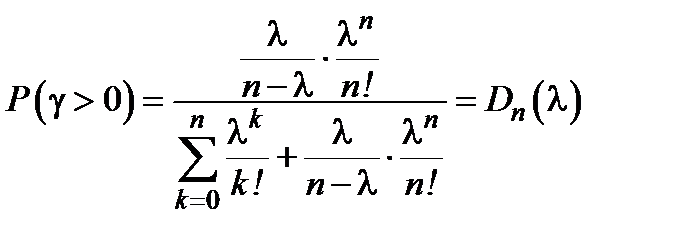7. Вероятность того, что период ожидания обслуживания вызова будет больше допустимого времени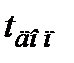 
;
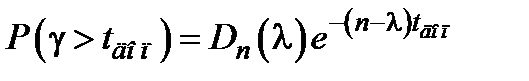
8. Средняя длина очереди
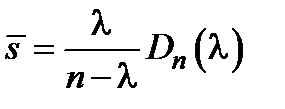
9. Среднее время ожидания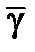 
– отношение среднего времени обслуживания вызовов к числу поступивших вызовов
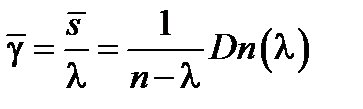
10. Среднее время ожидания обслуживания задержки вызова равно отношению суммарного времени ожидания обслуживания к числу задержки вызова.
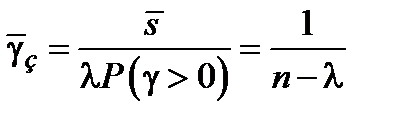
11. Число задержки вызовов
.
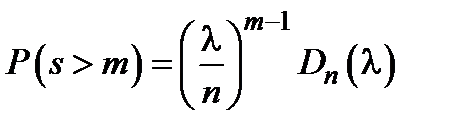Задание 1. На 4-канальную СМО с ожиданием поступает простейший поток вызовов с параметром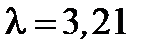 
. Необходимо:
1) Построить закон распределения числа поступивших вызовов.
2) Вычислить вероятность ожидания обслуживания поступивших вызовов.
3) Вычислить вероятность того, что период ожидания обслуживания вызова будет больше допустимого времени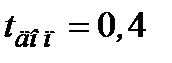 
.
4) Вычислить среднюю длину очереди
5) Вычислить среднее время ожидания.
6) Вычислить вероятность того, что длина очереди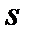 
будет больше, чем 5.
Решение. 1) Построим закон распределения числа поступивших вызовов.
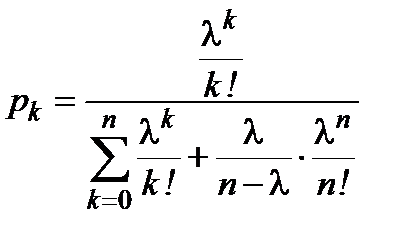
Вычислим
.
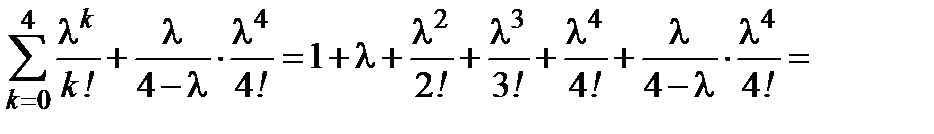
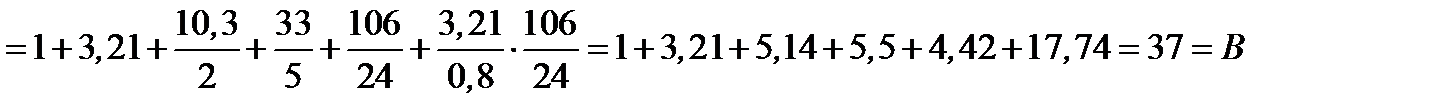Тогда
, 
,
, 
,
, 
,
, 
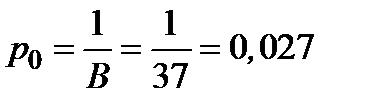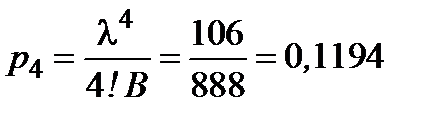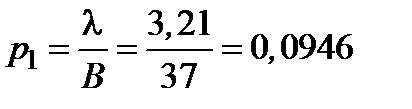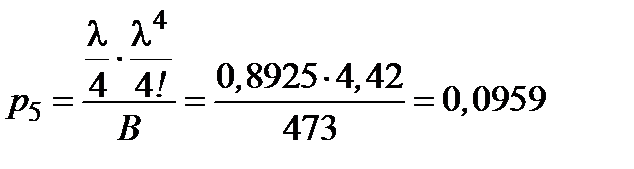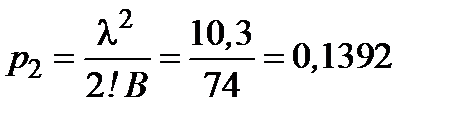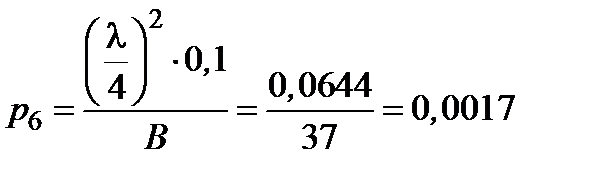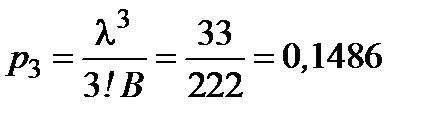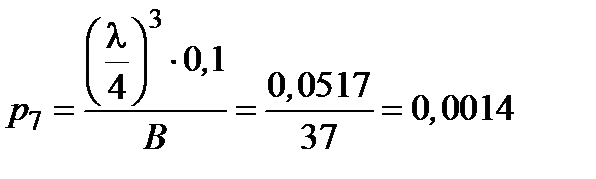
Проверим, что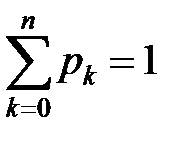 
:
.
Построим график закона распределения числа поступивших вызовов;
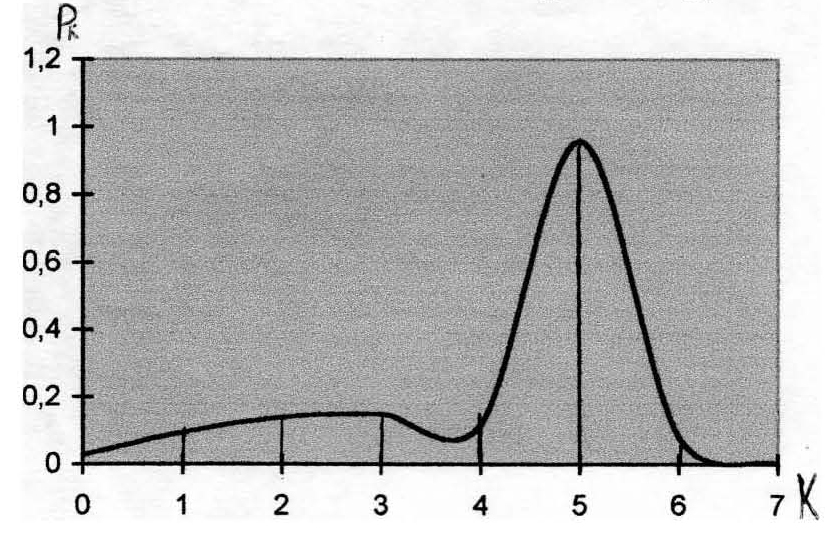
2) Вычислим вероятность ожидания обслуживания поступивших вызовов:
.
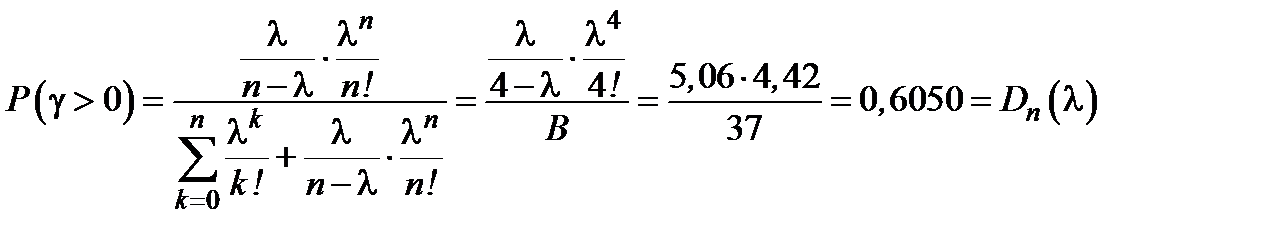3) Вычислим вероятность того, что период ожидания обслуживания вызова будет больше допустимого времени :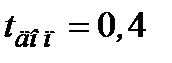
.
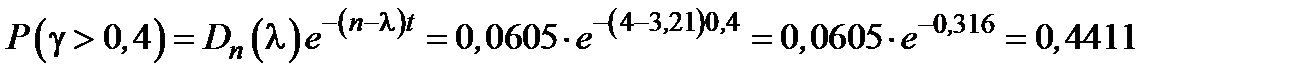4) Вычислим среднюю длину очереди:
.
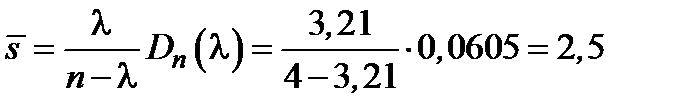5) Вычислим среднее время ожидания обслуживания:
.
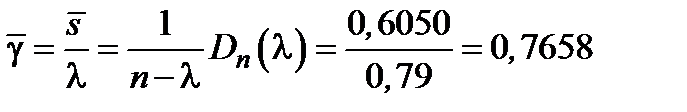6) Вычислим вероятность того, что длина очереди 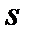будет больше, чем 5:
.
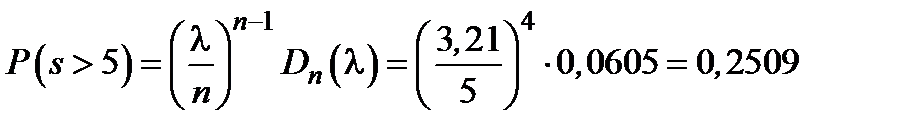