Статический расчет трехшарнирной арки.
Для определения вертикальных опорных реакций достаточно составить обычные уравнения равновесия в виде суммы моментов всех сил относительно опорных точек. Таким образом расчет опорных реакций аналогичен расчету опорных реакций эквивалентной балки т.е. балки с такой же нагрузкой [2, 4,6]. На Рис.4 дано изображение эквивалентной балки.
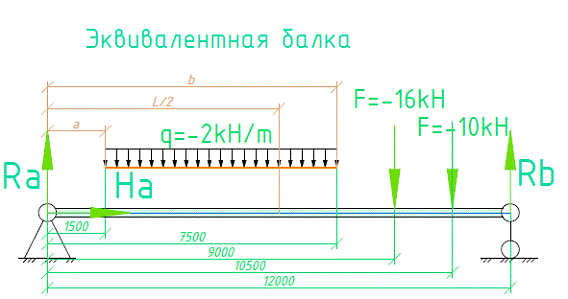
Рис.4 Расчетная схема эквивалентной балки.
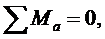
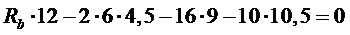
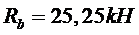
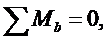
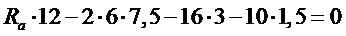
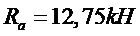
Горизонтальная составляющая реакций опор находится из условия равенства нулю изгибающего момента в шарнире “C”. Составляя уравнения равновесия в виде суммы моментов относительно шарнира “C” для левой части арки получим, искомую горизонтальную составляющую (распор)[2,6]. На Рис.5 дано изображение расчетной схемы для определения распора.
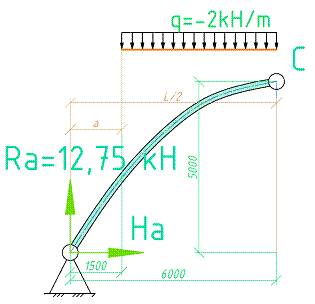
Рис.5 Расчетная схема для определения распора.
, 
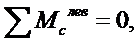
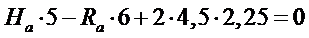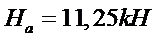
3. Определение внутренних силовых факторов в трехшарнирной арке
Для определения внутренних силовых факторов изгибающего момента -М, поперечной силы – Q, продольной силы- N воспользуемся методом сечений. На Рис.6 изображены внутренние силовые факторы, подлежащие определению.
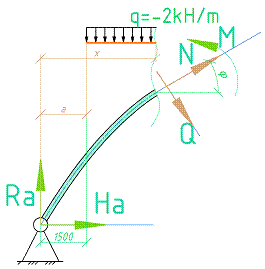Рис.6 Внутренние силовые факторы арки.
Рассмотрим равновесие элемента в виде суммы моментов относительно точки сечения, а также суммы проекций сил на ось, касательную к оси арки в точке сечения и сумму проекций сил на ось перпендикулярную оси арки в той же точке. Рис.6
Проведя вышеуказанные действия и после незначительных преобразований получим:
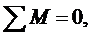
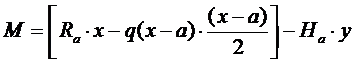(1) -изгибающий момент
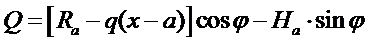(2) -поперечная сила;
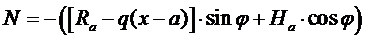(3) -продольная сила;
Рассмотрев в уравнении для изгибающего момента (1) выражение в скобках, нетрудно заметить, что это формула, позволяющая вычислить изгибающий момент в сечении эквивалентной балки Рис.4. В дальнейшем будем обозначать его -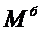 
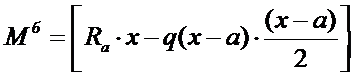(4)
Таким образом изгибающий момент в арке определится:
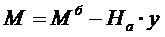(5)
Аналогичным образом значения для поперечной и продольной силы:
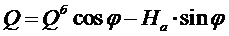; (6)
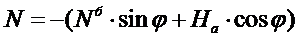(7)
Распор определится выражением: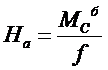 
[2,6].
Таким образом для определения внутренних силовых факторов трехшарнирной арки необходимо изначально определить значения факторов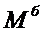 
, 
, 
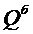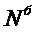для эквиваленто-нагруженной балки Рис.4. Далее воспользоваться зависимостями 5,6,7 и произвести окончательные вычисления
Определение значений и построения эпюр внутренних силовых факторов с использованием вычислительной среды Mathcad
Для начала создания програмы зададим положительные направления внешних силовых факторов, что и будем учитывать при составлении зависимостей. Это позволит создать унифицированную программу для расчета трехшарнирной арки при различных способах вертикального нагружения. Направления внешних силовых факторов будем задавать на эквивалентной балке [7].
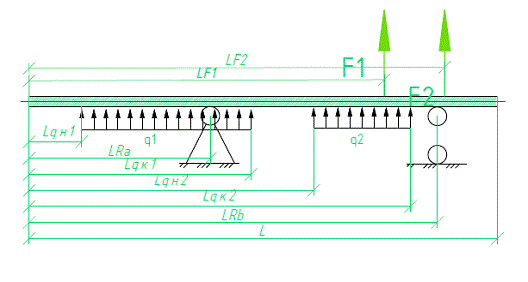
Рис.7 Положительные направления внешних силовых факторов.
На рис.7 указаны и условные обозначения всех элементов, которые будут представлены в программе.
Для задания исходных данных в среде Mathcad создадим размерный блок, в котором свяжем коэффициентами единицы измерения пользователя с величинами, заложенными в функционал Mathcad. Это делается, для автоматического определения размерности результата при вычислении [7].
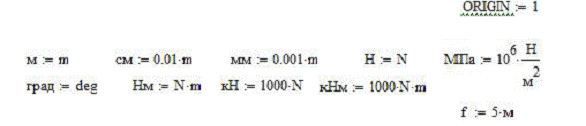
Далее задаем исходные данные в матричной форме:
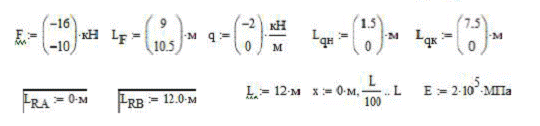
Переменную координату “x” задаем, как ранжированную переменную с шагом L/100 для более точного построения эпюр. Для расчета силовых факторов воспользуемся принципом независимого действия сил. Т.е. отдельно произведем расчет момента, поперечной и продольной силы от сосредоточенной нагрузки, отдельно от распределенной и отдельно от реакции опор. Математически это правило можно записать следующим образом:
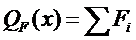; поперечная сила от действия сосредоточенных нагрузок.
Если распределенная нагрузка постоянной интенсивности приложена лишь на часть балки, то ее можно заменить двумя противоположными нагрузками: распределенной нагрузкой, приложенной от сечения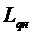 
до конца стержня, и фиктивной распределенной нагрузкой той же величины, но противоположного направления, приложенной от сечения 
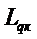до конца стержня[7,8]:
;
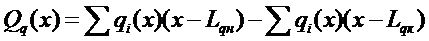Для записи внутренних усилий в общем виде в среде Mathcad удобно использовать булевы операторы условия. Булевы операторы принимают значения 1, если логическое выражение в скобках верно, и 0, если — не верно. Умножение какого-либо слагаемого на булев оператор условия позволяет включить это слагаемое, если условие выполняется, или выключить его, если условие не выполняется. Использование булевых операторов позволяет выстраивать довольно сложные математические выражения. Таким образом в программном виде уравнения для определения силовых факторов будут выглядеть:
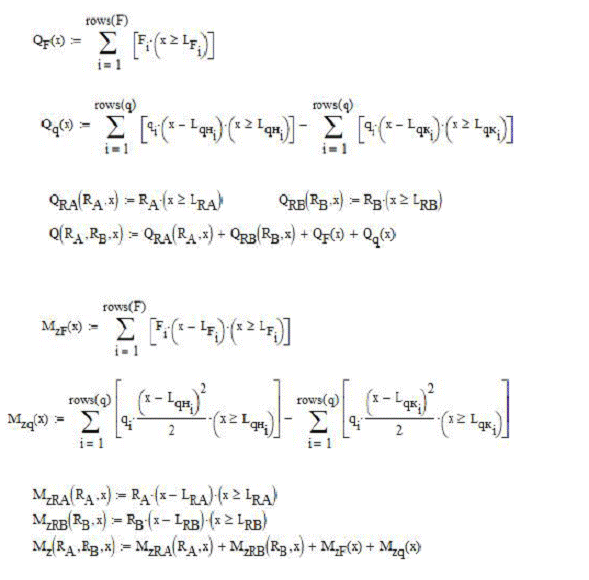
Для определения реакций опор воспользуемся функцией Find. Для расчета зададим некоторые начальные значения [7,8]:
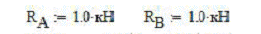
Эпюра изгибающих моментов и поперечной силы эквивалентной балки представлены на Рис.8
Для корректного отражения положительных значений изгибающего момента (положительный снизу) на оси ординат момент поставлен со знаком “минус”.
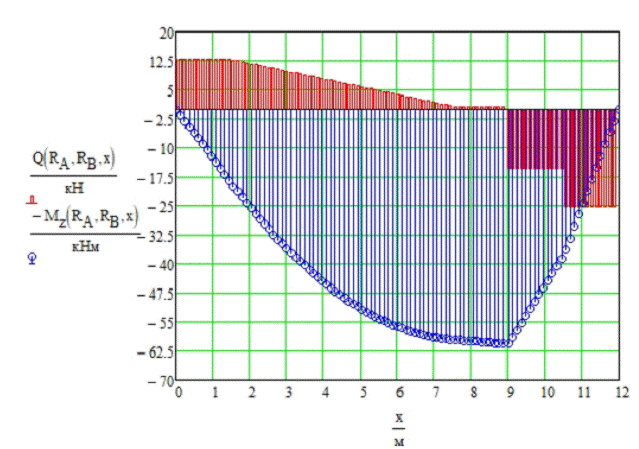
Рис.8 Эпюра изгибающих моментов и поперечной силы эквивалентной балки
Далее определяется значение распора и задается уравнение оси арки в координатах, начало которых совпадает с левой опорой арки.
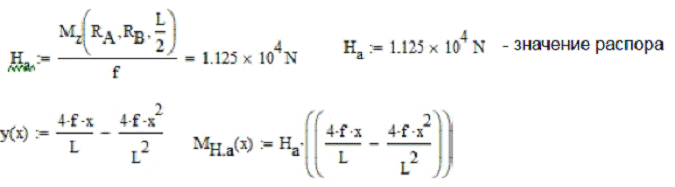
Эпюра добавляющей составляющей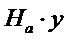 
момента арки представлена на рис.9
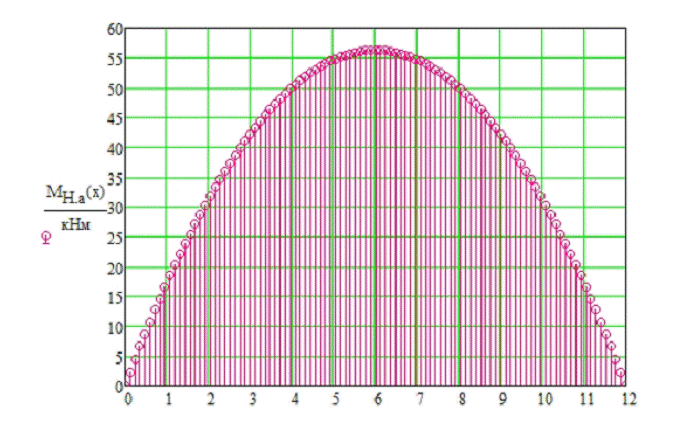
Рис.9Эпюра добавляющей составляющей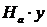 
момента арки
Выражение для определения итого изгибающего момента трехшарнирной арки будет выглядеть [7,8,9]:
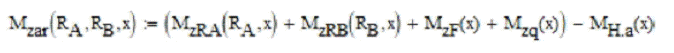
Итоговая эпюра изгибающего момента и ось арки представлена на рис.10
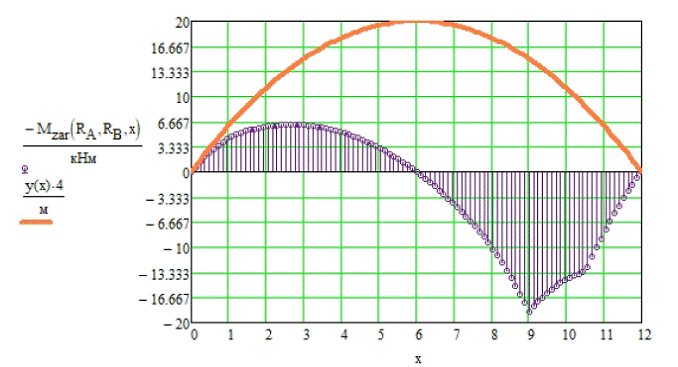
Рис.10 Итоговая эпюра изгибающего момента и ось арки.
Эпюры поперечной силы Q, продольной силы N, угла поворота φ и оси арки y(x) представлены на рис.11 [7,10].
Выражения для их определения:
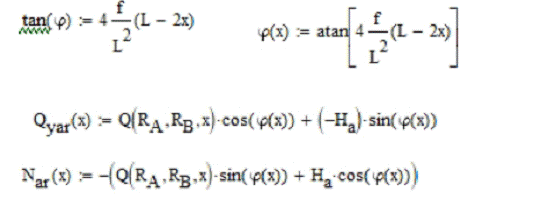
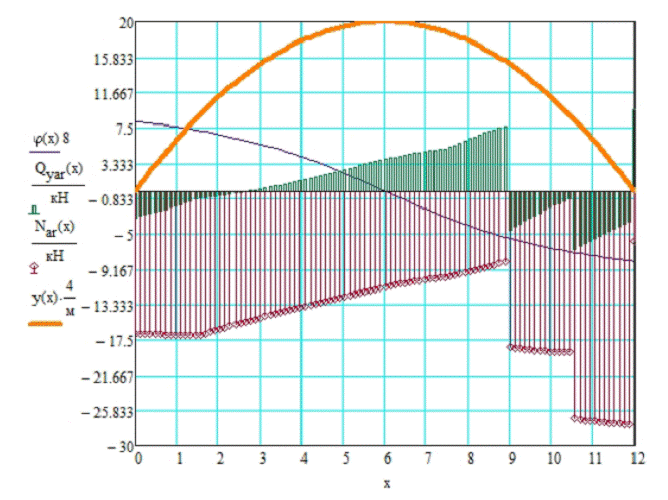
Рис.11 Эпюры поперечной силы Q, продольной силы N, угла поворота φ и оси арки y(x).
Литература
1. Ким Д.А. Роль купольных зданий в архитектуре будущего // Инженерный вестник Дона, 2018. №1. URL: ivdon.ru/ru/magazine/archive/n1y2019/5490
2. Соловей М.А., Мищенко О.А. Расчет плоских статически определимых систем. Киев: КНУБА, 2014. С. 2-44.
3. Igor A. Karnovsky Theory of Arched Structures. Strength, Stability, Vibration. London: Springer, 2012. pp. 19-26.
4. Чепурненко А.С., Андреев В.И., Языев Б.М. Построение модели равнопрочной многопролетной балки // Инженерный вестник Дона, 2013. №1. URL: ivdon.ru/ru/magazine/archive/n1y2013/1571
5. Соловей М.А., Мищенко О.А., Свешников О.Г. Кинематический анализ стержневых систем. Киев: КНУБА, 2012. С. 4-44.
6. Анохин Н.Н., Строительная механика в примерах и задачах. Часть 1. 4-е изд. М: Издательство АСВ, 2016. С. 7-90.
7. Макаров Е.Г., Сопротивление материалов на базе Mathcad. СПб: БХВ-Петербург, 2004. С. 61-183.
8. Каганов В.И., Компьютерные вычисления в средах Exel и Mathcad. 2-е изд. М: Горячая линия-Телеком, 2015. С. 173-209.
9. Wei Lu, Ding Zhou, Zhi Chen Practical Calculation of Cable-Stayed Arch Bridge Lateral Stability // scientific.net. 2014. №9. pp. 1586-1592.
10. Черняк А.А., Черняк Ж.А., Ю.А Доманова Ю.А., Высшая математика на базе Mathcad общий курс. СПб: БХВ-Петербург, 2004. С. 209-280.
References
1. Kim D.A. Inženernyj vestnik Dona (Rus). 2018. №1. URL: ivdon.ru/ru/magazine/archive/n1y2018/4687
2. M.A. Solovej, O.A. Mishchenko Raschet ploskih staticheski opredelimyh sistem.[ The calculation of the plane statically determinate systems]. Kiev: KNUBA, 2014. pp. 2-44.
3. Igor A. Karnovsky Theory of Arched Structures. Strength, Stability, Vibration. London: Springer, 2012. pp. 19-26.
4. A.S. CHepurnenko, V.I. Andreev, B.M. Inženernyj vestnik Dona (Rus). 2013. №1. URL: ivdon.ru/ru/magazine/archive/n1y2013/157
5. M.A. Solovej, O.A. Mishchenko, O.G. Sveshnikov Kinematicheskij analiz sterzhnevyh sistem.[ Kinematic analysis of rod systems] Kiev: KNUBA, 2012. pp. 4-44.
6. Anohin N.N. Stroitel'naya mekhanika v primerah i zadachah. CHast' 1.
[Construction mechanics in examples and tasks. Part1] 4-e izd. M: Izdatel'stvo ASV, 2016. pp. 7-90.
7. Makarov E.G. Soprotivlenie materialov na baze Mathcad.[Strength of materials based on Mathcad] SPb: BHV-Peterburg, 2004. pp. 61-183.
8. Kaganov V.I Komp'yuternye vychisleniya v sredah Exel i Mathcad. [Computer calculations in the software packages Excel and Mathcad] 2-e izd. M: Goryachaya liniya-Telekom, 2015. pp. 173-209.
9. Wei Lu, Ding Zhou, Zhi Chen Practical Calculation of Cable-Stayed Arch Bridge Lateral Stability // scientific.net. 2014. №9. pp. 1586-1592.
10. CHernyak A.A, CHernyak ZH.A, Domanova YU.A Vysshaya matematika na baze Mathcad obshchij kurs.[Higher mathematics on the base of Mathcad. General course] SPb: BHV-Peterburg, 2004. pp. 209-280.