Несобственные интегралы
ПММ, 1 курс, 9 группа, Спицын А. С.
Перед решением любого несобственного интеграла важно проверить подынтегральную функцию на непрерывность.
Несобственные интегралы 1-го рода
1. Бесконечный верхний предел интегрирования: 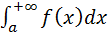
A. Обобщение формулы Ньютона-Лейбница
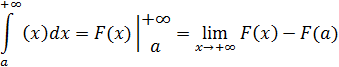
Алгоритм решения:
1. Проверить непрерывность функции на промежутке интегрирования.
2. Найти неопределённый интеграл.
3. Подставить верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница.
Пример 1:
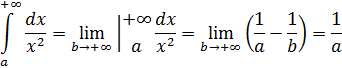
Пример 2 (№ 2338, Демидович):
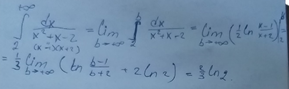
B. Замена переменной
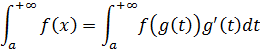
Алгоритм решения:
1. Проверить непрерывность функции на промежутке интегрирования.
2. Ввести замену и преобразовать исходный интеграл согласно формуле.
3. Полученный интеграл вычислить с помощью формулы Ньютона-Лейбница (см. предыдущий пункт)
Пример 3:
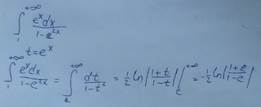
C. Внесение функции под знак дифференциала
Алгоритм аналогичен предыдущим, однако вместо замены переменной при поиске первообразной используем метод внесения функции под знак дифференциала.
Пример 4:
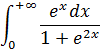
Функция непрерывна на исследуемом отрезке, найдём несобственный интеграл:
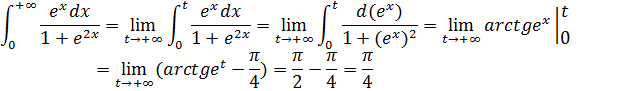
D. Интегрирование по частям
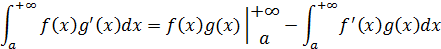
Алгоритм решения:
1. Проверить непрерывность функции на промежутке интегрирования.
2. Применить формулу интегрирования по частям.
3. Вычислить необходимые пределы и несобственные интегралы.
Пример 5:
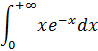
Подынтегральное выражение позволяет применить метод интегрирования по частям:
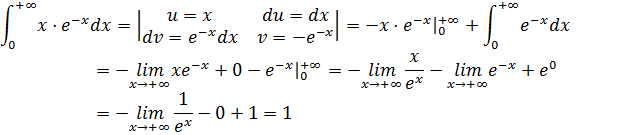
E. Пример несуществования интеграла
Пример 6:
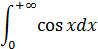
Данного несобственного интеграла не существует, так как
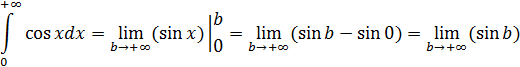
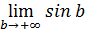
в свою очередь не существует.
2. Бесконечный нижний предел интегрирования: 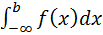
Общий алгоритм:
· найти первообразную (неопределённый интеграл)
· использовать предел при вычислении интеграла
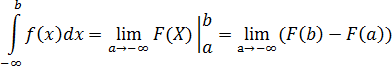
Пример 7:
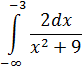
Подынтегральная функция непрерывна на (– ∞; –3]. Найдём несобственный интеграл, используя уже известные методы и устремив нижний предел к – ∞.
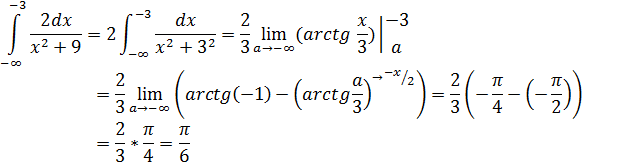
3. Бесконечные пределы интегрирования (и верхний, и нижний): 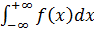
Методика: представить в виде суммы двух несобственных интегралов
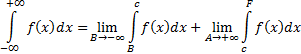
Пример 8:
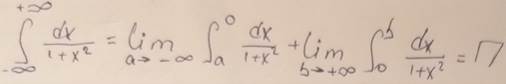
Пример 9:
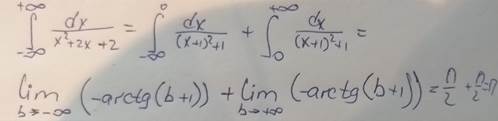
Метод решения несобственного интеграла от четной функции по симметричному относительно нуля отрезку
Пример 10:
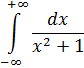
Подынтегральная функция является чётной. В несобственных интегралах с бесконечными пределами (а значит, симметричным интервалом интегрирования) чётностью пользоваться можно. Промежуток выгодно споловинить, а результат – удвоить:
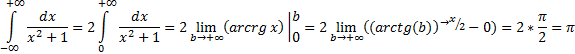
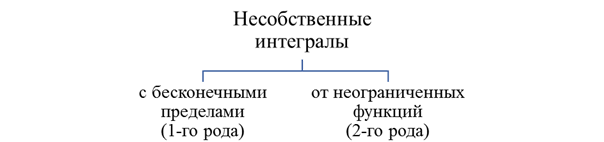
Несобственные интегралы 2-го рода
1. Подынтегральная функция не существует в т. x=a
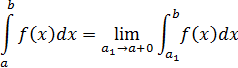
Алгоритм решения:
1. Поверить пределы интегрирования, подставив в подынтегральную функцию.
2. Вычислить неопределённый интеграл, используя известные методы.
3. Подставляем верхний и нижний предел по модифицированной формуле Ньютона-Лейбница, устремив предел к значению а справа.
4. Вычислить полученное выражение.
Пример 11:
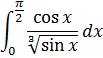
Подынтегральная функция не определена в т. х=0. Следовательно, функция не ограничена в правосторонней окрестности точки х=0.
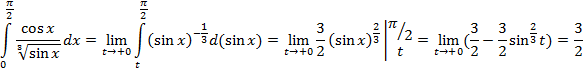
2. Подынтегральная функция не существует в т. x=b
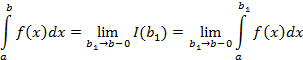
Алгоритм решения аналогичен предыдущему, единственное отличие в стремлении предела к значению b слева.
Пример 12:
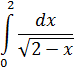
Функция непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому