Процедуры сглаживания
Пример 1. В табл. 1 отражена динамика доходов предпринимателя, не так давно зарегистрировавший фирму «Альтернативный отдых», владеющую сетью киосков, в которых осуществляется прокат видеокассет и торговля аудиокассетами. Требуется для 1-го столбца таблицы рассчитать значения: 1) скользящей средней (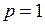
); 2) скользящей средней (
); 2) взвешенной скользящей средней (
). Построить и проанализировать совмещенный график скользящих средних и фактических данных.
Т а б л и ц а 1
Динамика доходов фирмы «Альтернативный отдых»
| Месяц | Доход от проката видеокассет, р. | Доход от продажи аудиокассет, р. |
Решение с помощью Excel
1. Ввод исходных данных.
2. Расчет значений:
1) скользящей средней ()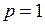
;
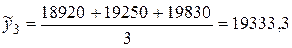и т.д.
2) скользящей средней ()
;
и т.д.;
3) взвешенной скользящей средней ()
;
и т.д.
Оформление результатов всех расчетов в виде табл. 2.
Т а б л и ц а 2
Скользящие средние
| Месяц | Доход от проката видеокассет | Скользящая средняя | Взвешенная скользящая средняя | |
|
|
|
| ||
| – | – | – | ||
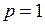
| 19043,3 | – | – | ||
| 19333,3 | – | 19326,3 | ||
| 19576,7 | 19336,7 | 19663,7 | ||
| 19706,7 | 19512,9 | 19698,9 | ||
| 19816,7 | 19746,7 | 19707,7 | ||
| 20193,3 | 19976,2 | 20189,1 | ||
| 20556,7 | 20221,4 | 20659,1 | ||
| 20720,0 | 20408,1 | 20741,1 | ||
| 20810,0 | 20633,8 | 20777,7 | ||
| 20883,3 | 20881,9 | 20836,6 | ||
| 21286,7 | 21125,2 | 21244,9 | ||
| 21553,3 | 21335,2 | 21603,7 | ||
| 21896,7 | – | 21940,9 | ||
| 22026,7 | – | – | ||
| – | – | – |
3. Построение для исходных и сглаженных значений доходов от проката видеокассет графиков, используя для этого «Мастер диаграмм» (см. рис. 1). Графический ряд, сглаженный по семилетней скользящей средней, носит более гладкий характер. Это объясняется тем, что чем больше длина интервала сглаживания, тем более гладкий ряд получается на выходе модели. Наиболее точно изгибы кривой фактических данных повторяет, благодаря весовым коэффициентам, взвешенная скользящая средняя.
Рис. 1. Сглаженные и фактические значения дохода от проката видеокассет
Задание 1. По данным табл. 1 рассчитайте сглаженные значения ряда, характеризующего динамику доходов предпринимателя от продажи аудиокассет с использованием скользящей средней (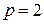
) и взвешенной скользящей средней (
). Постройте совмещенный график по исходным и сглаженным данным. Сравните между собой сглаженные кривые, сделать вывод относительно методов сглаживания. Вычислите абсолютные приросты и относительные темпы прироста для исходных и сглаженных данных. Постройте для них диаграммы и сравнить между собой. Рассчитайте по исходным и сглаженным данным средний абсолютный прирост за рассматриваемый период.
Типы роста и трендовые модели
Пример 3. Ежемесячно фирма «Канцелярская ниша» на основе информации об объемах продаж составляет планы закупок отдельных групп товаров для своих магазинов. В текущем месяце на ее складе заканчиваются цветные карандаши, в связи с чем отделу закупок фирмы было поручено определить количество упаковок, которое необходимо заказать на оптовой базе канцтоваров.
Специалисты отдела закупок обычно принимают решение на основе предоставляемой аналитическим отделом информации о прогнозных оценках объемов продаж на последующие три месяца. Следовательно, аналитическому отделу фирмы предстоит решить три задачи: 1) подобрать кривую роста (трендовую модель) к временному ряду табл. 7, отражающему динамику объема продаж цветных карандашей фирмой за последние 15 месяцев; 2) с помощью критерия Дарбина – Уотсона проверить адекватность выбранной для целей прогнозирования модели; 3) получить точечные и интервальные прогнозы объема продаж на 3 месяца. Требуется решить поставленные перед аналитическим отделом фирмы задачи.
Т а б л и ц а 7
Динамика объема продаж фирмы «Канцелярская ниша»
| Месяц | Бумага, руб. | Альбомы, шт. | Блокноты, руб. | Ватман, руб. | Калькуляторы, руб. | Карандаши, упаковок | Календари, руб. | Маркеры, шт. | |
| 12228,10 | 1988,95 | 1315,50 | 2562,34 | 2987,01 | |||||
| 12277,75 | 2475,05 | 1635,75 | 5042,50 | 2986,95 | |||||
| 12335,21 | 2996,21 | 1858,95 | 7510,28 | 2985,57 | |||||
| 12390,65 | 3659,34 | 2023,57 | 9942,23 | 2984,95 | |||||
| 12450,12 | 4717,23 | 2163,58 | 12362,01 | 2983,88 | |||||
| 12507,79 | 5729,17 | 2248,90 | 14785,35 | 2982,69 | |||||
| 12565,45 | 7458,35 | 2344,02 | 17183,03 | 2981,16 | |||||
| 12625,76 | 9375,78 | 2422,18 | 19588,33 | 2980,23 | |||||
| 12677,44 | 11486,75 | 2485,76 | 21978,19 | 2979,12 | |||||
| 12740,34 | 14825,89 | 2534,75 | 24362,34 | 2970,18 | |||||
| 12800,57 | 18235,78 | 2600,56 | 26751,38 | 2938,79 | |||||
| 12860,14 | 23436,73 | 2647,21 | 29122,78 | 2860,75 | |||||
| 12905,05 | 28272,65 | 2690,45 | 31499,93 | 2647,73 | |||||
| 12949,15 | 36050,78 | 2735,46 | 33869,17 | 2065,86 | |||||
| 13003,12 | 46692,12 | 2775,85 | 36234,77 | 491,24 |
Решение с помощью Excel
1. Ввод исходных данных по объему продаж цветных карандашей.
2. Расчет абсолютных приростов 
по исходным данным 
и оформление результатов расчетов в виде табл. 8.
Т а б л и ц а 8
Абсолютные приросты
|
|
|
|
|
|
| 801,13 | 1582,65 | 137,46 | |||
| 859,23 | 58,1 | 1722,41 | 139,76 | ||
| 938,27 | 79,04 | 1880,44 | 158,03 | ||
| 1015,27 | 2045,77 | 165,33 | |||
| 1106,56 | 91,29 | 2219,39 | 173,62 | ||
| 1211,15 | 104,59 | 2404,3 | 184,91 | ||
| 1326,03 | 114,88 | 2589,6 | 185,3 | ||
| 1445,19 | 119,16 |
3. Определение типа роста по «Линейчатой» диаграмме, построенной для абсолютных приростов.
Рис. 3.Абсолютные приросты продаж цветных карандашей
Как показывает анализ диаграмм, временной ряд, характеризующий объем продаж цветных карандашей, имеет тенденцию увеличивающегося роста. Известно, что для моделирования такого типа роста можно использовать следующие модели:
и 
.
4. Подготовка исходных данных для построения указанных моделей и оформление их в виде табл. 9.
Т а б л и ц а 9
Данные для построения моделей
|
| 
|
| 
|
|
|
|
|
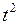
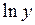
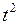
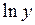
| 801,13 | 6,69 | 1582,65 | 7,37 | ||||
| 859,23 | 6,76 | 1722,41 | 7,45 | ||||
| 938,27 | 6,84 | 1880,44 | 7,54 | ||||
| 1015,27 | 6,92 | 2045,77 | 7,62 | ||||
| 1106,56 | 7,01 | 2219,39 | 7,7 | ||||
| 1211,15 | 7,1 | 2404,3 | 7,79 | ||||
| 1326,03 | 7,19 | 2589,6 | 7,86 | ||||
| 1445,19 | 7,28 |
5. Нахождение коэффициентов трендовых моделей с помощью «Пакета анализа» Excel (см. Вывод итогов 1 и Вывод итогов 2).
Таким образом, в рассматриваемом случае парабола имеет вид
.
Поскольку
; 
,
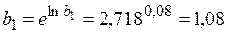то в рассматриваемом случае показательная модель записывается следующим образом:
.
| ВЫВОД ИТОГОВ 1 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,9999875 | |||||
| R-квадрат | 0,999975 | |||||
| Нормированный R-квадрат | 0,9999708 | |||||
| Стандартная ошибка | 3,1338086 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 240019,9 | 2,44E-28 | ||||
| Остаток | 117,8491 | 9,820757 | ||||
| Итого | ||||||
| Коэффи-циенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 747,61277 | 2,791389 | 267,8282 | 4,94E-24 | 741,5309 | 753,6947 |
| Переменная X 1 | 46,860806 | 0,802812 | 58,37084 | 4,22E-16 | 45,11163 | 48,60998 |
| Переменная X 2 | 5,0886304 | 0,048791 | 104,2937 | 4,04E-19 | 4,982323 | 5,194938 |
| ВЫВОД ИТОГОВ 2 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,9998213 | |||||
| R-квадрат | 0,9996426 | |||||
| Нормированный R-квадрат | 0,9996151 | |||||
| Стандартная ошибка | 0,0075111 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 2,051269 | 2,051269 | 36358,94 | 8,56E-24 | ||
| Остаток | 0,000733 | 5,64E-05 | ||||
| Итого | 2,052002 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 6,5895102 | 0,004081 | 1614,586 | 7,45E-36 | 6,580693 | 6,598327 |
| Переменная X 1 | 0,0855918 | 0,000449 | 190,6802 | 8,56E-24 | 0,084622 | 0,086562 |
6. Вычисление расчетных значений объема продаж по построенным моделям и оформление результатов в виде табл. 10.
7. Расчет отклонений расчетных значений и фактических, их квадратов и средних квадратических отклонений. Оформление результатов в виде табл. 11.
Минимальное среднее квадратическое отклонение дает парабола, поэтому она выбирается в качестве тренда.
Т а б л и ц а 10
Расчетные значения объема продаж
|
|
| 
| 
|
|
|
|
|
| 801,13 | 799,56 | 792,43 | 1582,65 | 1581,54 | 1571,58 | ||
| 859,23 | 861,69 | 863,24 | 1722,41 | 1725,08 | 1712,02 | ||
| 938,27 | 933,99 | 940,38 | 1880,44 | 1878,81 | 1865,01 | ||
| 1015,27 | 1016,47 | 1024,42 | 2045,77 | 2042,71 | 2031,67 | ||
| 1106,56 | 1109,13 | 1115,96 | 2219,39 | 2216,78 | 2213,22 | ||
| 1211,15 | 1211,97 | 1215,68 | 2404,3 | 2401,04 | 2411,00 | ||
| 1326,03 | 1324,98 | 1324,32 | 2589,6 | 2595,47 | 2626,45 | ||
| 1445,19 | 1448,17 | 1442,66 |
Т а б л и ц а 11
Среднеквадратические отклонения
|
|
|
| 
| 
|
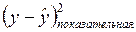
| 801,13 | 799,56 | 792,43 | 2,4580 | 75,7191 |
| 859,23 | 861,69 | 863,24 | 6,0462 | 16,0879 |
| 938,27 | 933,99 | 940,38 | 18,2939 | 4,4587 |
| 1015,27 | 1016,47 | 1024,42 | 1,4498 | 83,6409 |
| 1106,56 | 1109,13 | 1115,96 | 6,6181 | 88,3400 |
| 1211,15 | 1211,97 | 1215,68 | 0,6696 | 20,5462 |
| 1326,03 | 1324,98 | 1324,32 | 1,0998 | 2,9305 |
| 1445,19 | 1448,17 | 1442,66 | 8,8897 | 6,3944 |
| 1582,65 | 1581,54 | 1571,58 | 1,2341 | 122,5496 |
| 1722,41 | 1725,08 | 1712,02 | 7,1496 | 107,9803 |
| 1880,44 | 1878,81 | 1865,01 | 2,6702 | 238,1671 |
| 2045,77 | 2042,71 | 2031,67 | 9,3929 | 198,8850 |
| 2219,39 | 2216,78 | 2213,22 | 6,8028 | 38,0646 |
| 2404,30 | 2401,04 | 2411,00 | 10,6562 | 44,8528 |
| 2589,60 | 2595,47 | 2626,45 | 34,4182 | 1357,7565 |
| Сумма квадратов отклонений | 117,8491 | 2406,3736 | ||
| Средний квадрат отклонений | 7,8566 | 160,4249 | ||
| Среднее квадратическое отклонение | 2,8030 | 12,6659 |
8. Подготовка данных для расчета числителя критерия Дарбина – Уотсона в виде табл. 12.
Т а б л и ц а 12
Данные для расчета критерия Дарбина – Уотсона
|
|
|
| 
| 
|
| 801,13 | 799,56 | 1,5678 | ||
| 859,23 | 861,69 | -2,4589 | 16,2143 | |
| 938,27 | 933,99 | 4,2771 | 45,3743 |
Окончание табл. 12
| 1015,27 | 1016,47 | -1,2041 | 30,0438 | |
| 1106,56 | 1109,13 | -2,5726 | 1,8727 | |
| 1211,15 | 1211,97 | -0,8183 | 3,0774 | |
| 1326,03 | 1324,98 | 1,0487 | 3,4857 | |
| 1445,19 | 1448,17 | -2,9816 | 16,2430 | |
| 1582,65 | 1581,54 | 1,1109 | 16,7484 | |
| 1722,41 | 1725,08 | -2,6739 | 14,3246 | |
| 1880,44 | 1878,81 | 1,6341 | 18,5585 | |
| 2045,77 | 2042,71 | 3,0648 | 2,0469 | |
| 2219,39 | 2216,78 | 2,6082 | 0,2085 | |
| 2404,3 | 2401,04 | 3,2644 | 0,4306 | |
| 2589,6 | 2595,47 | -5,8667 | 83,3768 | |
| Числитель критерия Дарбина – Уотсона | 252,0053 |
9. Окончательный расчет критерия Дарбина – Уотсона
.
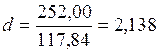При 5%-ном уровне значимости для 15 наблюдений и двух переменных в модели нижняя граница критерия 
, а верхняя – 
. Так как 
, то с критическим значениям сравнивается не сам коэффициент 
, а 
, равный 
. Таким образом, 
и гипотеза о независимости случайных отклонений не отвергается, т.е. построенная модель адекватна.
10. Расчет прогнозных оценок и их доверительных границ, учитывая, что 
. Оформление результатов в виде табл. 13.
Т а б л и ц а 13
Прогнозные оценки объема продаж и их доверительные границы
| Месяц | Прогнозные оценки объема продаж | Нижняя граница прогнозной оценки | Верхняя граница прогнозной оценки |
| 2800,08 | 2792,18 | 2807,97 | |
| 3014,86 | 3006,53 | 3023,19 | |
| 3239,82 | 3230,98 | 3248,67 |
Пример 4. Фирма «Золотое перо», осуществляющая оптовую продажу канцтоваров, некоторое время тому назад начала реализовывать шариковые ручки новой модели. Динамика спроса на них представлена в табл. 14. Знакомство с данными этой таблицы обеспокоило руководство фирмы, поскольку приросты объема продаж с определенного момента начали уменьшаться. Поэтому аналитическому отделу было поручено провести более глубокий анализ имеющихся данных. Специалисты этого отдела сразу же выдвинули гипотезу о том, что закон изменения этих данных описывается кривой Гомперца. Кроме того, руководство фирмы поставило перед аналитиками задачу прогнозирования увеличения спроса на ручки на следующие два месяца в случае, если спрос в настоящее время не достиг своего максимального объема. Таким образом, требуется: 1) проверить гипотезу, выдвинутую аналитическим отделом; 2) построить графики по фактическим и расчетным значениям; 3) указать максимально возможную величину спроса; 4) получить прогнозные оценки объема продаж на два месяца, если в этом есть смысл.
Т а б л и ц а 14
Динамика спроса на шариковые ручки, реализуемые фирмой «Золотое перо»
| Месяц | Спрос на ручки, тыс. шт. | Месяц | Спрос на ручки, тыс. шт. |
Решение с помощью Excel
1. Ввод исходных данных.
2. Логарифмирование значений и оформление результатов расчетов в виде табл. 15.
Т а б л и ц а 15
Логарифмированные значения спроса
|
|
|
|
|
|
|
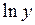
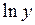
| 0,00 | 5,01 | ||||
| 2,30 | 5,11 | ||||
| 3,04 | 5,18 | ||||
| 2,94 | 5,16 | ||||
| 3,69 | 5,18 | ||||
| 4,16 | 5,25 | ||||
| 4,56 | 5,23 | ||||
| 4,74 | 5,25 | ||||
| 4,77 | 5,26 |
3. Разбиение последнего столбца табл. 15 на три группы по 6 наблюдений (6 месяцев) в каждой и нахождение суммы значений каждой этой группы
; 
; 
.
4. Определение коэффициентов модели кривой Гомперца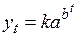 
;
;
;
.
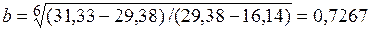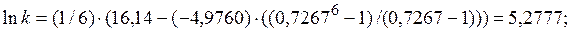
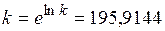Таким образом, кривая Гомперца имеет вид:
.
5. Определение расчетных значений и оформление результатов в виде табл. 16.
Т а б л и ц а 16
Расчетные значения спроса
|
|
| 
|
|
|
|
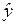
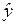
6. Построение с помощью мастера диаграмм графика по фактическим и расчетным значениям (см. рис. 4).
Рис. 4. Совместный график фактической и расчетной
динамики спроса на шариковые ручки
Анализ рис. 4 позволяет подтвердить гипотезу аналитиков о том, что закон изменения данных табл. 14 действительно описывается кривой Гомперца.
7. Расчет прогнозных оценок спроса на шариковые ручки. Учитывая, что фактическое значение спроса в настоящее время (17-й период) составляет 192000 шариковые ручки, а максимально возможный объем (см. значение коэффициента 
) – 195000 шт., можно сделать вывод о том, что спрос пока не достигает своего максимального значения, а следовательно, имеет смысл прогнозировать объемы продаж на следующие месяцы
; 
.
Задание 3. По данным табл. 7 для каждого товара, кроме цветных карандашей, определить тип роста временного ряда, отражающего динамику соответствующего объема продаж. Применяя среднеквадратический критерий, определить среди функций, используемых для моделирования данного типа роста, наиболее подходящую для прогнозных расчетов. С помощью критерия Дарбина – Уотсона проверить адекватность прогнозной модели и получить точечные и интервальные прогнозы на четыре периода. Построить «точечный» график для фактических и расчетных значений, включая прогнозные.
Задание 4. Руководство компании ОАО «Искусный град», основной деятельностью которой является строительство оригинальных жилых домов в г. Воронеж, с целью определения стратегии своей деятельности на последующие два периода поручило специалистам в области экономического анализа рассчитать прогнозные оценки ввода в эксплуатацию жилья на эти периоды. Один из специалистов сделал предположение о том, что динамика имеющихся для прогноза данных (см. в табл. 17), скорее всего, описывается кривой Перла – Рида. Проверьте правильность этого предположения, построив графики по фактическим и расчетным значениям, а затем получите прогнозные оценки ввода в эксплуатацию жилья на два периода.
Т а б л и ц а 17
Динамика ввода жилья в эксплуатацию, тыс. кв. м
| Квартал | Ввод в эксплуатацию | Квартал | Ввод в эксплуатацию |
| 4,8 | 100,6 | ||
| 18,6 | 112,3 | ||
| 18,7 | 104,8 | ||
| 41,9 | 107,9 | ||
| 55,6 | 112,6 | ||
| 62,1 | 113,8 | ||
| 79,3 | 114,5 | ||
| 76,4 |