Тесты по теории вероятностей и математической статистике

Группа А. Выберите один или несколько правильных ответов из приведенных вариантов. Если нет вариантов ответов – укажите правильный ответ самостоятельно.

 

1. Вероятность достоверного события равна …

2. Вероятность невозможного события равна …

3. Вероятность практически достоверного события равна …

1)

0,99

2)

0,01

3)

4)

4. Укажите вероятность практически невозможного события

1)

0,99

2)

0,01

3)

4)

5. Известно, что Р(А) = 0,65. Укажите вероятность противоположного события

1)

-0,65

2)

0,5

3)

0,65

4)

0,35

6. Сумма вероятностей событий, образующих полную группу равна …

 

7. Монету подбросили два раза. Вероятность того, что герб выпал один раз равна …

8. Монету подбросили три раза. Вероятность того, что герб выпал один раз равна …

1)

1/9

2)

1/3

3)

3/8

4)

1/8

9. Укажите вероятность события: при подбрасывании игральной кости выпадет число очков, большее 4 …

10. Бросили два игральных кубика. Вероятность того, что сумма очков больше 10 равна …

1)

10/36

2)

5/36

3)

2/36

4)

3/36

11. Укажите вероятность события: из урны, в которой 6 белых, 4 черных и 10 красных шаров, наугад достали красный шар…

12. На отрезок [0; 1] наудачу брошена точка с координатой x. Вероятность того, что координата х окажется больше 0.6, равна …

 

13. В урне находится 1 белый и 2 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара белые, равна …

1)

1/9

2)

1/6

3)

2/3

4)

2/9

14. Урна содержит 6 белых и 9 черных шаров. Вероятность достать первым белый шар, а вторым черный, равна (шар в урну не возвращается)

1)

6/25

2)

9/35

3)

3/5

4)

2/5

15. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,9 и 0,4 соответственно. Вероятность того, что в цель попадут оба стрелка, равна …

16. В урне 3 белых и 7 черных шаров. Из урны одновременно достали два шара. Вероятность того, что оба шара черные равна… (результат округлить до сотых)

Ответ: 0,47

17. Монету подбрасывают до тех пор, пока не выпадет орел. Вероятность того, что монету подбросят точно три раза равна…

Ответ: 0,125

18. В урне 8 белых и 10 черных шаров. Из урны наугад достали три шара. Вероятность того, что среди них точно один белый шар равна …

1)

5/34

2)

15/34

3)

8/18

4)

8/10

19. В урне 5 белых и 7 черных шаров. Из урны наугад достали три шара. Вероятность того, что среди них хотя бы один белый шар равна …

1)

5/12

2)

5/7

3)

37/44

4)

7/44

 

20. В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…

1)

0,45

2)

0,15

3)

0,4

4)

0,9

21. Событие А может наступить лишь при условии появления одного из двух несовместных событий и , образующих полную группу событий. Известны вероятность и условные вероятности , . Тогда вероятность равна …

1)

3/4

2)

1/2

3)

1/3

4)

2/3

 

22. Укажите значение суммы …

23. Стрелок стреляет по мишени 10 раз. Вероятность попадания при одном выстреле р = 0,8. Вероятность того, что будет точно 8 попаданий равна …

1)		4)
2)		5)
3)		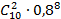6)

24. Стрелок стреляет по мишени 10 раз. Вероятность попадания при одном выстреле р = 0,75. Вероятность того, что будет не менее 9 попаданий равна …

1)		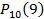3)
2)		4)

 

25. Задан ряд распределения случайной величины Х:

Х	-1
P	0,1	?	0,3

Значение 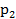равно …

26. Случайная величина Х задана законом распределения

Х
P	0,2	0,3	0,5

Укажите возможные значения случайной величины Х²

1)	0, 1	3)	2, 4, 6
2)	1, 4, 9	4)	0, 1, 2, 3, 4

27. Дискретные случайные величины Х и Y заданы законами распределения

Х	-1				Y
P	0,1	0,3	0,6		P	0,7	0,3

Вероятность того, что случайная величина Х+Y примет значение 1 равна …

1)

0,24

2)

0,7

3)

0,03

4)

0,21

28. Дискретная случайная величина Х задана законом распределения вероятностей

Х	-2
Р	0,2	0,3	0,5

Математическое ожидание M (X) равно…

29. Дискретная случайная величина Х задана законом распределения вероятностей

Х	-1
Р	0,4		0,5

Математическое ожидание M (X) равно…

1)

0,1

2)

3)

1,5

4)

1,3

30. Дискретная случайная величина Х задана законом распределения вероятностей

Х	-1
Р	0,2	0,1	0,7

Значение 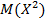равно …

Ответ: 0,9

31. Известно, что , , , , , 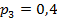M (X) = 5,6. Значение равно …

1)

2)

3)

4)

32. Установите соответствие между числовыми характеристиками и формулами, по которым они вычисляются для дискретной случайной величины

а)	Математическое ожидание	1)
b)	Дисперсия	2)
		3)
		4)

33. Дискретная случайная величина Х задана законом распределения вероятностей

Х	-1
P	0,2	0,8

Дисперсия Х равна

1)

0,6

2)

0,64

3)

4)

0,8

34. 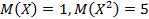. Среднее квадратическое отклонение равно …

Ответ: 2

35. Выберите свойства математического ожидания случайной величины

a.

b.

c.

d.

e.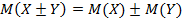

Ответ: b,c,e

36. Выберите свойства дисперсии случайной величины

a.

b.

c.

d.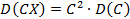

e.

Ответ: a,d

37. Выражение равно …

Ответ: 0

38. Дискретная случайная величина Х задана законом распределения вероятностей

Х
Р	0,3	0,1	0,6

Значение F(2) равно …

Ответ: 0,3

39. Стрелок стреляет по мишени 5 раз. Случайная величина Х – количество попаданий в мишень. Значение F(6) равно …

Ответ: 1

40. Укажите справедливые утверждения для функции распределения случайной величины

1)		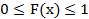3)		5)		7)
2)		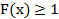4)		6)		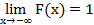8)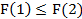

41. Укажите справедливые утверждения для непрерывной случайной величины (F(x) – интегральная функция распределения, j(x) – дифференциальная функция распределения)

1)		3)		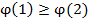5)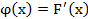
2)		4)		6)

42. Случайная величина Х задана функцией распределения

Вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0; 1/3) равна…

1)

2)

1/3

3)

3/4

4)

1/4

43. Случайная величина Х задана плотностью распределения 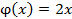в интервале (0;1). Вне этого интервала 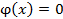. Математическое ожидание величины Х равно …

1)

1/2

2)

2/3

3)

1/3

4)

1/4

44. Формула вычисления дисперсии непрерывной случайной величины

a.

b.

c.

d.

Ответ: d

45. Х – непрерывная случайная величина, принимающая значения из промежутка [0;100]. Значение вероятности равно …

Ответ: 0

46. Непрерывная случайная величина равномерно распределена на отрезке 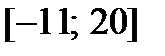. Вероятность равна …

1)

11/32

2)

5/16

3)

10/31

4)

11/31

47. Нормально распределенная случайная величина Х задана плотностью вероятности

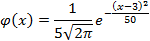
Математическое ожидание Х равно …

Ответ: 3

48. Нормально распределенная случайная величина Х задана плотностью вероятности

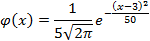
Дисперсия Х равна …

Ответ: 25

49. Значение интеграла от плотности распределения стандартной нормально распределенной величины равно…

Ответ: 0,5

50. Нормально распределенная случайная величина Х задана плотностью вероятности

Вероятность равна …

1)

0,3413

2)

0,6827

3)

0,9545

4)

0,9973

 

 

51. Объем выборки 1, 2, 2, 2, 3, 3, 3, 3, 4 равен …

Ответ: 9

52. Дана выборка 1, 2, 2, 2, 3, 3, 4, 4, 4, 6. Укажите варианту, частота которой равна 2

Ответ: 3

53. Дана выборка 1, 2, 2, 2, 2, 3, 4, 4, 4, 6. Укажите варианту, относительная частота которой равна 0,3

Ответ: 4

54. Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид

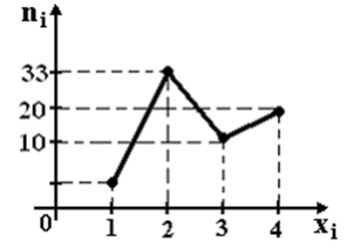
Тогда число вариант в выборке равно …

1)

2)

3)

4)

55. Дана выборка 1, 2, 2, 2, 2, 3, 4, 4, 4, 6. Мода равна …

Ответ: 2

56. Дана выборка 1, 2, 2, 2, 2, 3, 4, 4, 4, 6. Медиана равна …

Ответ: 2,5

57. Дана выборка 5, 5, 7, 9, 9, 9, 25. Медиана равна …

Ответ: 9

58. Дана выборка 1, 2, 2, 2, 2, 3, 4, 4, 4, 6. Среднее выборочное равно …

Ответ: 3

59. Дана выборка 1, 2, 2, 2, 2, 3, 4, 4, 4, 6. Размах равен …

Ответ: 5

60. Произведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 12. Тогда несмещенная оценка математического ожидания равна …

1)

8,25

2)

8,5

3)

4)

61. Дана выборка объема n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее …

1)	Не изменится	2)	Увеличится в 25 раз
3)	Уменьшится в 5 раз	4)	Увеличится в 5 раз

62. Дана выборка -1, 0, 2, 7. Выборочная дисперсия равна …

1)

2)

9,5

3)

4)

13,5

63. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 3, 4, 5, х. Если выборочная дисперсия равна 3,5, то значение x равно

1)

-8

2)

3)

4)

64. Выборочная дисперсия вариационного ряда равна 3,5. Объем выборки равен 50. Исправленная выборочная дисперсия равна …

1)

3,43

2)

3,57

3)

0,07

4)

3,5

65. Если все варианты х_i исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия

a. Увеличится в три раза

b. Увеличится в девять раз

c. Увеличится в 81 раз

d. Не изменится

Ответ: d

66. Для некоторого количественного признака известно, что и . Коэффициент вариации количественного признака равен

1)	60%	2)	167%	3)	250%	4)	150%
5)	10%	6)	2,5%	7)	1,5%

67. Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид…

1)

(10,5; 11,5)

2)

(11; 11,5)

3)

(10,5; 10,9)

4)

(10,5; 11)

68. Дан доверительный интервал (12,44;14,68) для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна:

1)

0,01

2)

1,12

3)

2,24

4)

13,56

69. Дан доверительный интервал (32,06; 41,18) для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна:

1)

9,12

2)

36,52

3)

36,62

4)

73,24

70. Построен доверительный интервал для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при уменьшении объема выборки в два раза значение точности этой оценки

a. Увеличится в два раза

b. Уменьшится в два раза

c. Увеличится в раз

d. Уменьшится в раз

Ответ: с

71. Дан доверительный интервал (16,64; 18,92) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид:

1)

(16,15;19,41)

2)

(16,15;18,38)

3)

(17,18;18,38)

4)

(17,18; 18,92)

72. Пусть – совместно независимые стандартные нормальные случайные величины, т.е. , тогда случайная величина

имеет …

a. Распределение Стьюдента

b. Распределение Фишера

c. Распределение Хи-квадрат

d. Показательное распределение

Ответ: с

73. Пусть 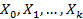– независимые стандартные нормальные случайные величины, такие что . Укажите распределение случайной величины

a. Распределение Стьюдента

b. Распределение Фишера

c. Распределение Хи-квадрат

d. Показательное распределение

Ответ: а

74. Основная гипотеза имеет вид . Тогда конкурирующей может являться гипотеза

a.

b.

c.

d.

Ответ: с

75. Основная гипотеза имеет вид . Тогда конкурирующей может являться гипотеза

a.

b.

c.

d.

Ответ: b

76. Ошибка первого рода при проверке статистической гипотезы

a. Отвергнуть нулевую гипотезу, если она верна

b. Принять нулевую гипотезу, если она неверна

c. Отвергнуть альтернативную гипотезу

d. Принять альтернативную гипотезу

Ответ: а

77. Соотношением вида 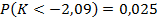можно определить

a. Левостороннюю критическую область

b. Правостороннюю критическую область

c. Двустороннюю критическую область

d. Область принятия гипотезы

Ответ: а

78. Правосторонняя критическая область может определяться из соотношения

a.

b.

c.

d.

Ответ: а

79. Соотношением вида можно определить

a. Левостороннюю критическую область

b. Правостороннюю критическую область

c. Двустороннюю критическую область

d. Область принятия гипотезы

Ответ: с

80. Распределение, используемое при применении критерия Пирсона

a. Распределение Стьюдента

b. Распределение Фишера

c. Распределение Хи-квадрат

d. Показательное распределение

Ответ: с