Применение функций обработки данных к векторам и матрицам
Ранее мы познакомились с функциями, предназначенными для создания и изменения структуры векторов и матриц. В пакете Matlab также имеются функции, предоставляющие возможность обработки элементов векторов и матриц. Эти функции позволяют вычислить сумму или произведение элементов, отсортировать данные, найти среднее, максимальное и минимальные значения элементов вектора или матрицы.
Полный список функций обработки можно получить набрав:
>> help datafun
Полезные функции:
>> size(A) % определяет размер массива
В случае вектора выводится количество элементов, а в случае матрицы – количество строк и столбцов.
Количество измерений можно получить:
>> ndims(A)
Функции для векторов
Пусть имеем вектор X
>> X=[9 2 3 4 15 6 1 7 ];
Рассмотрим некоторые функции.
Сумма элементов вектора:
>> sum(X)
ans =
Произведение элементов вектора:
>> prod(X)
ans =
Максимальное значение вектора:
>> max(X) % возвращает первое наибольшее, если есть одинаковые
ans =
Максимальное значение вектора и его номер:
>> [m,k]=max(X)
m =
k =
Минимальное значение вектора:
>> min(X)
ans =
Минимальное значение вектора и его номер:
>> [m,k]=min(X)
m =
k =
Среднее арифметическое элементов вектора:
>> mean(X)
ans =
5.8750
Сортировка элементов вектора по возрастании:
>> sort(X)
ans =
1 2 3 4 6 7 9 15
Для сортировки элементов вектора по убыванию можно воспользоваться той же функцией:
>> Х= - sort(-X)
Х =
15 9 7 6 4 3 2 1
Или
Sort(X,'descend')
Разворот вектора на 90°
>>rot90(X)
Эта функция разворачивает вектор против часовой стрелки. В результате получаем вектор-столбец:
ans =
Для векторов и матриц используются функции с одинаковыми названиями (sum, mean, prod, max, min, …), с той лишь разницей, что в матрице действия выполняются не во всей матрице, а в каждом столбце (или в каждой строке).
Пусть имеем матрицу А
>> A=[1 2 3;4 5 6;7 8 9];
A =
1 2 3
4 5 6
7 8 9
Рассмотрим эти функции.
Сумма элементов
Сумма элементов в столбцах матрицы:
>> sum(A)
ans =
12 15 18
Или можно использовать при обращении два аргумента sum(A, 1)= sum(A)
При применении этой функции к матрице, ML вычисляет сумму элементов в столбцах и выдает вектор-строку размером, равным числу столбцов матрицы, а каждый элемент вектора равен сумме элементов соответствующего столбца матрицы.
Для получения суммы элементов в строках матрицы в команде указывается 2-й входной аргумент или признак – 2. Введем команду:
>> sum(A, 2)
ans =
Результат – вектор-столбец, каждый элемент которого равен сумме элементов соответствующей строки.
Для векторов результат не зависит от формы вектора (столбец или строка)
Пусть имеем вектор X
>> X=[9 2 3 4 15 6 1 7 ];
Сумма элементов вектора:
>> sum(X)
ans =
>> sum(X’)
ans =
Получение из матрицы вектора
>> A(:) %результат – вектор столбец в порядке следования по столбцам
ans =
Для получения вектора-строки можно записать:
>> A(:)'
ans =
1 4 7 2 5 8 3 6 9
Для получения суммы всех элементов матрицы можно использовать команду
>>sum(sum(A)) или sum(A(:))
ans =
Для вычисления произведения правила такие же. По умолчанию произведение считается по столбцам.
Произведение элементов матрицы по столбцам:
>> prod(A)
ans =
28 80 162
Произведение элементов матрицы по строкам:
>> prod(A,2)
ans =
или
>> prod(A')
ans =
6 120 504
Функции сумма и произведение можно использовать, например, для вычисления произведения и суммы чисел от 2 до 5
>> prod(2:5)
ans =
>> sum(2:5)
ans =
В функциях для вычисления суммы, произведения и последующих функциях для элементов матрицы результатом будет вектор-строка, число элементов которой равно числу столбцов матрицы.
Есть функции, которые выдают наибольшее и наименьшее значения в столбцах матрицы. Результат – вектор-строка. При нахождении наибольшего и наименьшего значения в строках матрицы результат – вектор - столбец
Максимальное значение в каждом столбце:
>> max(A) или >> max(A, 1)
ans =
7 8 9 % результат – вектор из максимумов каждого столбца
Максимальное значение в каждой строке:
>> max(A')
ans =
3 6 9
или так
>> max(A, [], 2) % результат – вектор столбец
% [] - пустой второй параметр
ans =
Максимаум во всей матрице
>> max(max(A)) или max(A(:))
ans =
max(X,Y) сравнивает 2 матрицы X и Y, returns an array the same size as X and Y with the largest elements taken from X or Y. Either one can be a scalar.
Наименьшее значение:
>> min(A) %в столбцах
ans =
1 2 3
>> min(A') %в строках
ans =
1 4 7
или
>> min(A, [],2) %результат – вектор столбец
ans =
Можно не только найти минимальное и максимальное значения, но и позиции этих элементов:
>> [m,k]=min(A)
Результат – два вектора, один из минимального или максимального значений в столбцах матрицы, а второй – из позиций этих элементов в соответствующем столбце:
m =
1 2 3
k =
1 1 1
>> [m,k]=max(A)
m =
7 8 9
k =
3 3 3
Наибольшее и наименьшее значение во всей матрице:
>>max(max(A)) или >> max(A(:))
>>min(min(A)) или >> min(A(:))
Среднее значение
Среднее арифметическое в столбцах. Результат – вектор-строка из средних арифметических в каждом столбц е:
>> mean(A)
ans =
4 5 6
или
>> mean(A,1)
ans =
4 5 6
В строках
>> mean(A, 2)
ans =
>> mean(A')
ans =
2 5 8
Сортировка.
Отсортировать вектор по возрастанию
sort(X)
по убыванию
sort(X,'descend') % Работает не во всех версиях
Сортировка элементов каждого столбца по возрастанию:
>>sort(A)
по убыванию
>> - sort(-A) или sort(X,'descend')
Сортировка элементов каждой строки по возрастанию:
>>sort(A,2)
Сортировка элементов каждой строки по убыванию
>> -sort(-A,2) или sort(X, 2, 'descend')
ans =
3 2 1
6 5 4
9 8 7
Разворот матрицы на 90°
Эта функция разворачивает матрицу на 90° против часовой стрелки:
>> rot90(A)
ans =
3 6 9
2 5 8
1 4 7
’’Зеркальное’’ отображение матрицы относительно вертикальной оси:
>> fliplr(A)
ans =
3 2 1
6 5 4
9 8 7
’’Зеркальное’’ отображение матрицы относительно горизонтальной оси:
>> flipud(A)
ans =
7 8 9
4 5 6
1 2 3
Примеры использования
При обработке векторов удобно использовать возможность выборки из вектора значений, отвечающим некоторому условию.
Например,
получить все отрицательные значения вектора.
>> X=[3 -4 5 -6 3 9 -5];
>> X(X<0)
ans =
-4 -6 -5
Получить все значения вектора из диапазона n, m.
>>X(X>=n && X <=m)
А теперь посмотрим, как применить такую конструкцию для нахождения среднего и суммы:
>> sum(X(X<0))
ans =
-15
>> mean(X(X<0))
ans =
-5
Сумма элементов, не принадлежащих диапазону
>> sum(X(X<=n || X >=m))
Найти наибольшее значение среди элементов <0
>> max(X(X<0))
ans =
-4
Для матрицы
>> X=[1 2 3; -4 8 -3; 9 -1 -2]
X =
1 2 3
-4 8 -3
9 -1 -2
Получить все элементы матрицы > p
>> p=6; X(X>p)
ans = % вектор значений в порядке следования по столбцам
Среднее значение всех положительных элементов матрицы
>> mean(X(X>0))
ans =
4.6000
Нормы матрицы
Сформируем матрицу заполнением случайными числами:
>> X=round(10*rand(4))-8*ones(4)
X =
1 -7 0 -6
2 -5 -6 -5
-3 0 1 -2
-7 -5 -5 -3
В математике норма матрицы может быть вычислена по разным формулам:
Найдем наибольшую сумму модулей элементов в столбцах матрицы

>> sum(abs(X))
ans =
13 17 12 16
>> max_stolb=max(sum(abs(X)))
max_stolb =
Найдем наибольшую сумму модулей элементов в строках матрицы 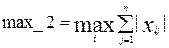
>> sum(abs(X),2)
ans =
>>max_str=max(sum(abs(X),2))
max_str =
Вычислить значение суммы модулей элементов матрицы по формуле

>> sum(abs(X)) %значение внутренней суммы
ans =
13 17 12 16
>> s1=sum(sum(abs(X))) или >>s1=sum(abs(X(:)))
s1 =
Вычислить:
Расчет евклидовой нормы подразумевает три действия: возведение каждого элемента в квадрат, суммирование и извлечение квадратной корня из общего результата

>> s=sqrt(sum(sum(abs(X).^2)))
s =
17.2627